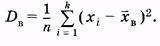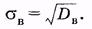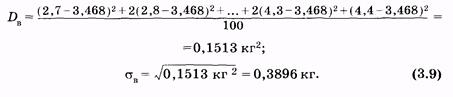Основные понятия математической статистики
Практическая работа №7
«Основы математической статистики. Элементы корреляционного анализа»
Цель занятия: Научиться решать примеры и задачи по данной теме
Вопросы теории ( исходный уровень)
1. Основные понятия математической статистики
2. Генеральная совокупность и выборка.
3. Вариационный и интервальный статистические ряды.
4. Полигон частот и гистограмма.
5. Точечная и интервальная оценка параметров генеральной совокупности по данным выборки.
6. Порядок статистической обработки экспериментальных данных.
7. Статистическая обработка данных лабораторного эксперимента.
8. Теория погрешностей.
9. Обработка результатов непосредственных и косвенных измерений
10. Правила оформления результатов лабораторных работ.
11. Элементы корреляционного анализа (лекция №2)
Содержание занятия:
1.ответить на вопросы по теме занятия
2.решить примеры
Задачи и примеры
Определить соответствие вариационного распределения измеренной величины нормальному закону распределения
- Произвести измерения N величин и записать результаты измерений в протокол.
- По результатам измерений построить вариационный ряд.
2.1.- в измеренных величинах найти величину ( хmin) с наименьшим значением и величину (хmax) с наибольшим значением.
2.2.-определить размах вариации R , представляющий собой разность между максимальной и минимальной вариантами совокупности ( R = xmax- xmin).
|
|
|
2.3.-по числу элементов совокупности N определим число классов К на которые следует разбить совокупность измеренных величин. При N≤100 К определим по формуле
K= 1+3,32 lg N, при N›100 К определим по формуле K= 5 lg N .
2.4.-определить величину классового интервала λ , как частное от деления размаха вариации R на число классов К , λ =R/К = (xmax- xmin)/ К.
Если окажется , что λ=1, собранный материал распределяется в безынтервальный вариационный ряд; если λ≠1, исходные данные необходимо распределить в интервальный ряд. При этом точность величины классового интервала должна соответствовать точности принятой при измерении величин.
2.5.- определить ширину классов входящих в интервальный вариационный ряд в которых расположатся все измеренные величины от xmax до xmin.
Ширина первого класса имеет протяженность от xmin до xmin+λ, т.е.[ xmin ÷ xmin+λ].
Ширина второго класса имеет протяженность от xmin+ λ +10-5λ до xmin+2λ , т.е.
[ xmin+ λ +10-5λ ÷ xmin+2λ] , где 10-5λ незначащее число и применяется для того, чтобы разграничить числа находящиеся на границе классовых интервалов и используется во всех классах для различия начала нового класса от конца предыдущего класса.
|
|
|
Ширина К-того класса имеет протяженность от xmin+(К-1) (λ +10-5λ ) до xmax, т.е.
[xmin+(К-1) (λ +10-5λ ) ÷ xmax], где xmax= xmin +К λ.
2.6.- найти среднее значение каждого класса хm . Среднее значение каждого класса равно полусумме значений начала и конца класса без незначащего числа 10-5λ, т.е.
хm=( xmin+(I-1) λ +xmin+Iλ)/2, где I принимает значения от 1 до К (I =1;2;…К).
2.7.- определить количество элементов n из измеренных N величин входящих в каждый класс, т.е. получить n1, n2,… nК
2.8. – определить относительную частоту рi попадания количества элементов ni из измеренных N величин в каждый класс, т.е. рi= ni/ N. Найти р1, р2,… рК.
- На основании пункта 2 заполнить таблицу:
| N= | ||||
| xmax= xmin= R = xmax- xmin= | ||||
| K= 1+3,32 lg N= | ||||
| λ =R/К = (xmax- xmin)/ К= | ||||
| Классные интервалы | 1 | 2 | … | К |
| Границы клас-сных интервалов | [ xmin ÷ xmin+λ] | [ xmin+ λ +10-5λ ÷ xmin+2λ] | … | [xmin+(К-1) (λ +10-5λ ) ÷ xmax] |
| Среднее значе-ние классного интервала хm | xmin+λ/2 | xmin+3λ/2 | … | xmin+(К+1)λ/2 |
| Количество ве-личин входящих в класс ni | n1 | n2 | … | nК |
| Частота попа-дания величин в класс рi= ni/ N | р1= n1/ N | р2= n2/ N | … | рК= nК/ N |
| (хm)I*pi | (xmin+λ/2)р1 | (xmin+3λ/2)р2 | … | (xmin+(К+1)λ/2)рК |
|
|
|
- По полученным данным построить графики вариационных рядов.
4.1. - полигон частот; по оси абсцисс откладывают среднее значение классов, по оси ординат частоту попадания величин в класс. Высота перпендикуляров, восставляемых на ось абсцисс, соответствует частоте классов. Соединяя вершины перпендикуляров прямыми линиями, получают геометрическую фигуру в виде многоугольника называемую полигоном распределения частот. Линия соединяющая вершины перпендикуляров, называют вариационной кривой или кривой распределения частот вариационного ряда.
4.2. – гистограмма; по оси абсцисс откладывают границы классовых интервалов , по оси ординат – частоты интервалов. В результате получается совокупность прямоугольников . т.е. гистограмма распределения.
4.3. – кумулята; по оси абсцисс откладывают среднее значение классов, по оси ординат – накопление частоты интервалов ( накопление частот находят последовательным суммированием или кумуляцией частот в направлении от первого класса до конца вариационного ряда , т.е. например в третьем классе накопленная частота будет соответствовать сумме частот трех классов) с последующим соединением точек прямыми линиями, получается график называемый кумулятой. Имеет вид S-образной кривой.
|
|
|
4.4. – огива; по оси абсцисс откладывают частоты , а по оси ординат значение классов с последующим соединением геометрических точек прямыми линиями, полученный график называют огивой.
При построении вариационной кривой масштабы на осях прямоугольных координат следует выбирать с таким расчетом, чтобы основание кривой было в 1,5 –2,0 больше ее высоты.
5. Определить основные характеристики варьирующих величин .
5.1. – средняя арифметическая  ; найти произведение среднего значения каждого класса (хevi) i на относительную частоту рi попадания количества элементов ni из измеренных N величин в каждый класс, т.е. рi*(хm)i. Найти р1*(хm) 1, р2*(хm)2,... рК*(хm)К. и по формуле определить среднее арифметическое
; найти произведение среднего значения каждого класса (хevi) i на относительную частоту рi попадания количества элементов ni из измеренных N величин в каждый класс, т.е. рi*(хm)i. Найти р1*(хm) 1, р2*(хm)2,... рК*(хm)К. и по формуле определить среднее арифметическое
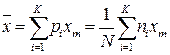
5.2. – дисперсия sx2 или σ2;
5.2.1. - найти отклонение среднего значение каждого класса хm от среднего арифметического  ,т.е. (хm)I-
,т.е. (хm)I-  ,
,
5.2.2. – возвести в квадрат отклонение среднего значение каждого класса хm от среднего арифметического  ,т.е.[ (хm)i-
,т.е.[ (хm)i-  ]2,
]2,
5.2.3. – умножить квадрат отклонений среднего значение каждого класса хm от среднего арифметического  на относительную частоту попадания в класс рi, т.е.
на относительную частоту попадания в класс рi, т.е.
[ (хm)i-  ]2*рi и по формуле определить дисперсию;
]2*рi и по формуле определить дисперсию;
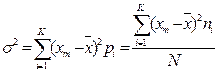

5.2.4.Установлено, что рассчитываемая по формуле дисперсия оказывается смещенной по отношению к своему генеральному параметру на величину , равную N/(N-1). Эта величина называется поправкой Бесселя. Разность (N-1)=k называют числом степеней свободы под которыми понимают число свободно варьирующих величин в составе численно ограниченной совокупности.
Несмещенная дисперсия и среднеквадратичное отклонение определяются;
5.2.4.1. – умножить квадрат отклонений среднего значение каждого класса хevi от среднего арифметического  на количество элементов n из измеренных N величин входящих в каждый класс, т.е. найти [ (хm)i-
на количество элементов n из измеренных N величин входящих в каждый класс, т.е. найти [ (хm)i-  ]2*ni и по формуле определить несмещенную дисперсию,
]2*ni и по формуле определить несмещенную дисперсию,
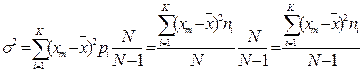
5.2.4.2. – среднее квадратическое отклонение sx есть показатель, представляющий корень квадратный из дисперсии,
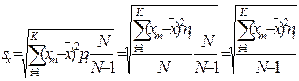
6.На основании пункта 5 заполнить таблицу:
| 1 | 2 | … | К | |
|
| ||||
(хm)I-  , ,
| (хm)1-  , ,
| (хm)2-  , ,
| … | (хm)К-  , ,
|
[ (хm)i-  ]2, ]2,
| [ (хm)1-  ]2 ]2
| [ (хm)2-  ]2 ]2
| … | .[ (хm)К-  ]2 ]2
|
умножить ква[ (хm)i-  ]2*рi ]2*рi
| [ (хm)1-  ]2*р1 ]2*р1
| [ (хm)2-  ]2*р2 ]2*р2
| … | [ (хm)К-  ]2*рК ]2*рК
|
| определить дисперсию |
| |||
[ (хm)i-  ]2*ni ]2*ni
| [ (хm)1-  ]2*n1 ]2*n1
| [ (хm) 2-  ]2*n2 ]2*n2
| [ (хm)К-  ]2*nК ]2*nК
| |
| определить несмещенную дисперсию, |
| |||
| Определить среднее квадратическое отклонение sx |
| |||
7. Определить соответствие вариационного распределения нормальному закону;
7.1. – найти нормированное отклонение t . Отклонение той или иной варианты от средней арифметической, отнесенное к величине среднего квадратического отклонения , называют нормированным отклонением и находят по формуле,
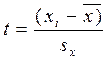
7.1. – Для соответствующих классов найдем функцию нормированного отклонения f(t) по таблице или по формуле, 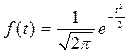
7.2. – найдем выравнивающие частоты вариационного ряда fI (t). Для того чтобы ордината выражала не вероятность, а абсолютные значения случайной величины, т.е. выравнивающие частоты вариант эмпирического распределения нужно fI (t) найти по формуле, 
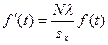
8. На основании пункта 7 заполним таблицу:
| 1 | 2 | … | К | |
| нормированное отклонение t | 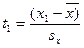
| 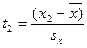
| … | 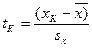
|
| нормированного отклонения f(t) | 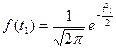
| 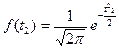
| … | 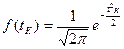
|
| выравнивающие частоты вариационного ряда fI (t) | 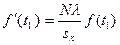
| 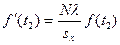
| … | 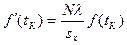
|
9. На графике полигона частот построить точки соответствующие выравнивающей частоте вариационного ряда, вычисленная по нормальному закону.
10. Записать значение исследуемой величины с границами доверительного интервала.
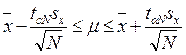
Таблица: Значения функции 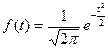
(ординаты нормальной кривой )
| t | Сотые доли t | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0 2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 2.9 3.0 3.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8 3.9 4,0 | 3989 3970 3910 3814 3683 3521 3332 3123 2897 2661 2420 2179 1942 1714 1497 1295 1109 0940 0790 0656 0540 0440 0356 0283 0224 0175 0136 0104 0079 0060 0044 0033 0024 0017 0012 0009 0006 0004 0003 0002 0001 | 3989 3965 3902 3802 3668 3503 3312 3101 2874 2637 2396 2155 1919 1691 1476 1276 1092 0925 0775 0644 0529 0431 0347 0277 0219 0171 0132 0101 0077 0058 0043 0032 0023 0017 0012 0008 0006 0004 0003 0002 0001 | 3989 3961 3894 3790 3653 3485 3292 3079 2850 2613 2371 2131 1895 1669 1456 1257 1074 0909 0761 0632 0519 0422 0339 0270 0213 0167 0129 0099 0075 0056 0042 0031 0022 0016 0012 0008 0006 0004 0003 0002 0001 | 3988 3956 3885 3778 3637 3467 3271 3056 2827 2589 2347 2107 1872 1647 1435 1238 1057 0893 0748 0620 0508 0413 0332 0264 0208 0163 0126 0096 0073 0055 0041 0030 0022 0016 0011 0008 0005 0004 0003 0002 0001 | 3986 3951 3876 3765 3621 3448 3251 3034 2803 2565 2323 2083 1849 1626 1415 1219 1040 0878 0734 0608 0498 0404 0325 0258 0203 0158 0122 0093 0071 0053 0039 0029 0021 0015 0011 0008 0005 0004 0003 0002 0001 | 3984 3945 3867 3752 3605 3429 3230 3011 2780 2541 2299 2059 1826 1604 1394 1200 1023 0863 0721 0596 0488 0396 0317 0252 0198 0154 0119 0091 0069 0051 0038 0028 0020 0015 0010 0007 0005 0004 0002 0002 0001 | 3982 3939 3857 3739 3589 3410 3209 2989 2756 2516 2275 2036 1804 1582 1374 1182 1006 0848 0707 0584 0478 0387 0310 0246 0194 0151 0116 0088 0067 0050 0037 0027 0020 0014 0010 0007 0005 0003 0002 0002 0001 | 3980 3932 3847 3726 3572 3391 3187 2966 2732 2492 2251 2012 1781 1561 1354 1163 0989 0833 0694 0573 0468 0379 0303 0241 0189 0147 0113 0086 0065 0048 0036 0026 0019 0014 0010 0007 0005 0003 0002 0002 0001 | 3977 3925 3836 3712 3555 3372 3166 2943 2709 2468 2227 1989 1758 1539 1334 1145 0973 0818 0681 0562 0459 0371 0297 0235 0184 0143 0110 0084 0063 0047 0035 0025 0018 0013 0009 0007 0005 0003 0002 0001 0001 | 3973 3918 3825 3697 3538 3352 3144 2920 2685 2444 2203 1965 1736 1518 1315 1127 0957 0804 0669 0551 0449 0363 0290 0229 0180 0139 0107 0081 0061 0046 0034 0025 0018 0013 0009 0006 0004 0003 0002 0001 0001 |
Лекция 2.
Элементы математической статистики. Случайная величина. Распределение дискретных и непрерывных случайных величин и их характеристики: математическое ожидание, дисперсия, среднее квадратичное отклонение. Примеры различных законов распределения. Нормальный закон распределения.
Генеральная совокупность и выборка. Гистограмма. Оценка параметров нормального распределения по опытным данным. Доверительные интервалы для средних. Интервальная оценка истинного значения измеряемой величины. Применение распределения Стьюдента для определения доверительных интервалов. Методы обработки медицинских данных.
Теория погрешностей, порядок обработка результатов прямых и косвенных измерений. Понятие о корреляционном анализе.
Математическая статистика
Методы математической статистики позволяют систематизировать и оценивать экспериментальные данные, которые рассматриваются как случайные величины.
Основные понятия математической статистики
В главе 2 были рассмотрены некоторые понятия и закономерности, которым подчинены массовые случайные явления. Одной из практических задач, связанных с этим, является создание методов отбора данных (статистические данные) из большой совокупности и их обработки. Такие вопросы рассматриваются в математической статистике.
Математическая статистика — наука о математиче ских методах систематизации и использования статистиче ских данных для решения научных и практических задач.
Математическая статистика тесно примыкает к теории вероятностей и базируется на ее понятиях. Однако главным в математической статистике является не распределение случайных величин, а анализ статистических данных и выяснение, какому распределению они соответствуют.
Предположим, что необходимо изучить множество объектов по какому-либо признаку. Это возможно сделать, либо проведя сплошное наблюдение (исследование, измерение), либо не сплошное, выборочное.
Выборочное, т. е. неполное, обследование может оказаться предпочтительнее по следующим причинам. Во-первых, естественно, что обследование части менее трудоемко, чем обследование целого; следовательно, одна из причин — экономическая. Во-вторых, может оказаться и так, что сплошное обследование просто нереально. Для того чтобы его провести, возможно, нужно уничтожить всю исследуемую технику или загубить все исследуемые биологические объекты. Так, например, врач, имплантирующий электроды в улитку для кохлеарного протезирования (см. § 6.5), должен иметь вероятностные представления о расположении улитки слухового аппарата. Казалось бы, наиболее достоверно такие сведения можно было получить при сплошном патологоанатомическом вскрытии всех умерших с производством соответствующих замеров. Однако достаточно собрать нужные сведения при выборочных измерениях.
Большая статистическая совокупность, из которой отбирается часть объектов для исследования, называется генеральной сово купностью, а множество объектов, отобранных из нее, — выбо рочной совокупностью, или выборкой.
Свойство объектов выборки должно соответствовать свойству объектов генеральной совокупности, или, как принято говорить, выборка должна быть представительной (репрезентативной). Так, например, если целью является изучение состояния здоровья населения большого города, то нельзя воспользоваться выборкой населения, проживающего в одном из районов города. Условия проживания в разных районах могут отличаться (различная влажность, наличие предприятий, жилищных строений и т. п.) и, таким образом, влиять на состояние здоровья. Поэтому выборка должна представлять случайно отобранные объекты.
Если записать в последовательности измерений все значения величины х в выборке, то получим простой статистический ряд. Например, рост мужчин (см): 170, 169, ... . Такой ряд неудобен для анализа, так как в нем нет последовательности возрастания (или убывания) значений, встречаются и повторяющиеся величины. Поэтому целесообразно ранжировать ряд, например, в возрастающем порядке значений и указать их повторяемость. Тогда статистическое распределение выборки:171, 172, 172, 168,
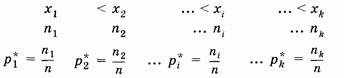
(3.1)
Здесь xi — наблюдаемые значения признака (варианта); ni — число наблюдений варианты xi (частота); рi* — относительная частота.
|
|
Общее число объектов в выборке (объем выборки)
всего k вариант. Статистическое распределение — это совокупность вариант и соответствующих им частот (или относительных частот), т. е. это совокупность данных 1-й и 2-й строки или 1-й и 3-й строки в (3.1).
В медицинской литературе статистическое распределение, состоящее из вариант и соответствующих им частот, получило название вариационного ряда.
Наряду с дискретным (точечным) статистическим распределением, которое было описано, используют непрерывное (интервальное) статистическое распределение:
|
|
(3.2)
Здесь xi -1 , xi - i -йинтервал, в котором заключено количественное значение признака; ni — сумма частот вариант, попавших в этот интервал; р * i — сумма относительных частот.
В качестве примера дискретного статистического распределения укажем массы новорожденных мальчиков (кг) и частоты (табл. 5).
Таблица 5
 |
Общее количество мальчиков (объем выборки)
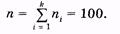 (3.3)
(3.3)
Можно это распределение представить и как непрерывное (интервальное) (табл. 6).
Таблица 6
| 2,65 — 2,75 | 2,75 — 2,85 | 2,85 — 2,95 | 2,95 — 3,05 | 3,05 — 3,15 | … |
| 1 | 2 | 7 | 8 | … |
Для наглядности статистические распределения изображают графически в виде полигона и гистограммы.
|
|
|
|
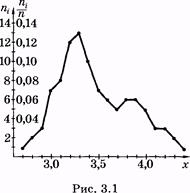
Полигон частот — ломаная линия, отрезки которой соединяют точки с координатами (х1, п1 , (х2; п2), ... или для полигона относительных частот — с координатами (х1; р1* ), (х2; р2 *), ... (рис. 3.1). Рис. 3.1 относится к распределению, представленному в табл. 5.
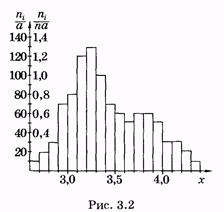
Гистограмма частот — совокупность смежных прямоугольников, построенных на одной прямой линии (рис. 3.2), основания прямоугольников одинаковы и равны а, а высоты равны отношению частоты (или относительной частоты) к а:
|
|
(3.4)
Таким образом, площадь каждого прямоугольника равна соответственно
|
|
|
|
Следовательно, площадь гистограммы частот 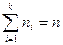 , а площадь гистограммы относительных частот
, а площадь гистограммы относительных частот
Наиболее распространенными характеристиками статистического распределения являются средние величины: мода, медиана и средняя арифметическая, или выборочная средняя.
Мода (Мо) равна варианте, которой соответствует наибольшая частота. В распределении массы новорожденных (см. табл. 5) Мо = 3,3 кг.
Медиана ( Me ) равна варианте, которая расположена в середине статистического распределения. Она делит статистический (вариационный) ряд на две равные части. При четном числе вариант за медиану принимают среднее значение из двух центральных вариант. В рассмотренном распределении (см. табл. 5) Me = 3,4 кг.
Выборочная средняя (хв) определяется как среднее арифметическое значение вариант статистического ряда:
|
|
(3.5)
|
|
Для примера (см. табл. 5)
|
|
Для характеристики рассеяния вариант вокруг своего среднего значения 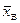 вводят характеристику, называемую выборочной дисперсией, — среднее арифметическое квадратов отклонения вариант от их среднего значения:
вводят характеристику, называемую выборочной дисперсией, — среднее арифметическое квадратов отклонения вариант от их среднего значения:
(3.7)
Квадратный корень из выборочной дисперсии называют выбороч ным средним квадратическим отклонением:
|
|
(3.8)
|
|
Для примера (см. табл. 5)
Дата добавления: 2019-02-13; просмотров: 325; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

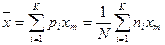
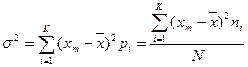
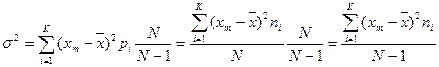
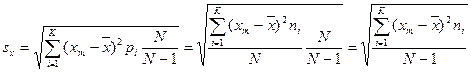
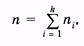

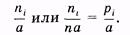
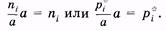
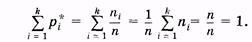
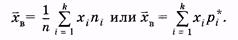
 (3.6)
(3.6)