ОСНОВНЫЕ СВОЙСТВА НЕОПРЕДЕЛЕННОГО

ИНТЕГРАЛА.

    Рассмотрим свойства неопределенного интеграла.

1.Производная от неопределенного интеграла равна подынтегральной функции:

(ò f(x)dx)¢ _x = f(x).

    По определению, ò f ( x ) dx = F ( x ) + C . Взяв производную от обеих частей, получим

(ò f(x)dx)¢ _x = (F(x) + C)¢ _x = F ¢ (x) = f(x).

    2. Дифференциал от неопределенного интеграла равен подынтегральному выражению (дифференциал уничтожает интеграл):

dò f(x)dx = f(x)dx.

    По определению, òf ( x ) dx = F ( x ) + C . Взяв дифференциал от обеих частей, получим

dò f(x)dx = d(F(x) + C) = dF(x) = F ¢ (x)dx = f(x)dx.

    3. Интеграл от дифференциала первообразной равен самой первообразной и дополнительному слагаемому С:

ò dF(x) = F(x) + C.

    Действительно,

ò dF ( x ) = ò F ¢ ( x ) dx = ò f ( x ) dx = F ( x ) + C .

    4. Постоянный множитель r можно вносить за знак неопределенного интеграла:

ò rf(x)dx =rò f(x)dx.

    Справедливость этого равенства проверяется дифференцированием его левой и правой частей

    5. Интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме интегралов от слагаемых:

ò (f₁(x) + f₂(x) – f₃(x))dx = ò f₁(x)dx + ò f₂(x)dx - ò f₃(x)dx.

    Это свойство доказывается также с помощью дифференцирования.

 

 

ОСНОВНЫЕ ФОРМУЛЫ ИНТЕГРИРОВАНИЯ.

    Приведем формулы, которые можно проверить дифференцированием.

1. ò dx = x + C.

2.

3.

4. ò a^xdx = a^x/ln a + C.

5. ò e^xdx = e^x + C.

6. ò cosxdx = sin x + C.

7. ò sin xdx = - cos x + C.

8.

9.

10.

11.

12. ò tg xdx = - ln |cos x| + C.

13. ò ctg xdx = ln |sin x| + C.

14.

15.

16.

17.

18.

19.

20.

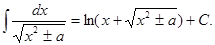
21.

22.

23.

24.

25.

26.

27.

28.

29.

 

ПРОСТЕЙШИЕ СПОСОБЫ ИНТЕГРИРОВАНИЯ.

    Непосредственное интегрирование. Способ непосредственного интегрирования основан на использовании свойств неопределенного интеграла и приведении подынтегрального выражения к табличной форме.

    Пример. Вычислить ò(2х³ – 3x² + 2х –7) dx .

    Решение. В данном примере под знаком интеграла стоит алгебраическая сумма функций. Согласно свойству 5 неопределенного интеграла.

ò(2х³ – 3х² +2х –7) dx = ò2 x ³ dx - ò3 x ² dx + ò2 xdx - ò7 dx .

    Последовательно применяя свойство 4 интегралов и формулы 1 и 2, получаем

ò(2х³ – 3х² + 2х – 7) dx = 2òx ³ dx -3òx ² dx + 2òxdx - 7òdx =

=

   

    Интегрирование подстановкой (заменой переменной). Этот способ заключается в переходе от данной переменной интегрирования к другой переменной для упрощения подынтегрального выражения и приведения его к одному из табличных.

    В интеграле ò f ( x ) dx сделаем подстановку x = j ( t ), где j ( t ) – функция, имеющая непрерывную производную. Тогда:

f ( x ) = f ( j ( t )); dx = j ¢ ( t ) dt ; ò f ( x ) dx = ò f ( j ( t )) j ¢ ( t ) dt .

    Пример. Вычислить ò sin ⁷ x cos xdx .

    Решение. Вычислим интеграл, использовав метод подстановки:

 

    Интегрирование по частям. Если и = и(х) и - дифференцируемые функции, то откуда Интегрируя последнее выражение, получаем

 

или

                                                                                (1)

Это и есть формула интегрирования по частям.

    Способ интегрирования по частям применяется в том случае, когда интеграл в правой части формулы (1) более прост для вычисления, чем исходный.

    Пример. Вычислить ò x ln xdx .

    Решение. Обозначим ln x через и тогда xdx = d u. Находим:

du = d ( ln x ) =   ò d u = ò xdx ;

---

Дата добавления: 2019-02-13; просмотров: 98; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!