КОДЫ БЧХ, ИСПРАВЛЯЮЩИЕ ДВЕ ОШИБКИ

Стр 1 из 2Следующая ⇒

Nbsp;

В.О. ОСИПЯН

Э Л Е М Е Н Т Ы

Т Е О Р И И П Е Р Е Д А Ч И И Н Ф О Р М А Ц И И

К Р А С Н О Д А Р 2 0 0 4

МИНИСТЕРСТВО ОБЩЕГО

И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

РОССИЙСКОЙ ФЕДЕРАЦИИ

КУБАНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

В . О . О С И П Я Н

Э Л Е М Е Н Т Ы

Т Е О Р И И П Е Р Е Д А Ч И И Н Ф О Р М А Ц И И

Учебное пособие

Краснодар 2 0 0 4

УДК 519.45

Элементы теории передачи информации : Учеб. пособие / В.О.Осипян;

Кубан. гос. ун-т. Краснодар, 1998. 37 с. ISBN 5-230-21822-3.

В пособии рассмотрены теоретические и практические вопросы основ теории передачи информации в целом. Адресовано студентам факультета прикладной математики специальности 010200, а также студентам других специальностей, интересующимся вопросами представления, надёжного хранения и эффективной обработки информации.

Печатается по решению редакционно-издательского совета

Кубанского государственного университета.

Рецензенты: кафедра прикладной математики (Кубанский государ- ственный технологический университет);

Н. Г. Колесников, проф. ( Кубанский государственный аграрный университет )

ISBN 5-230-21822-3 Ó Кубанский государственный

университет, 2004

ВВЕДЕНИЕ

Задача передачи, хранения и обработки информации в оптимальным заранее заданном смысле (например, для передачи информации с максимально возможной скоростью, для надёжного хранения информации, для представления информации в сжатом виде и т. д. ) в наше время при резком увеличении объёмов информации занимает особое место. Решение указанной задачи непосредственно связано с теорией передачи информации, так как хранение и обработка информации есть не что иное как передача информации во времени.

Данное учебное пособие написано на основе материалов лекций и практических занятий, которые в течение ряда лет читались автором в Кубанском государственном университете. Автор исходил из предположения, что студенты знакомы с основами дискретной математики и линейной алгебры. Дополнительные сведения из теории вероятностей можно найти в соответствующих источниках.

Пособие состоит из трёх глав. В первой главе приводится построение простых и составных полей Галуа - алфавит для дискретных логических и вычислительных устройств.

Вторая глава посвящена вопросам кодировании и передачи информации при наличии помех. Рассматриваются различные способы кодирования информации и сами коды, обнаруживающие и исправляющие канальные ошибки.

В третьей главе приводятся основные требования к представлению и передаче информации в каналах связи.

Приведённые в конце каждого параграфа задачи предназначены для понимания самого материала пособия.

АЛФАВИТ ДИСКРЕТНЫХ УСТРОЙСТВ. КОНЕЧНЫЕ ПОЛЯ

При изучении вопросов представления, хранения и переработки информации в качестве алфавита для дискретных логических и вычислительных устройств используется некоторое конечное поле или поле Галуа, которое состоит из конечного числа элементов в отличии от бесконечных полей. На практике чаще всего в качестве поля Галуа применяется поле, состоящее из двух элементов - 0 и 1.

1. 1. ПРОСТОЕ ПОЛЕ ГАЛУА GF( P )

Пусть Р простое число и * - произвольная арифметическая операция над целыми числами из Z по модулю Р. Тогда

GF( P ) = í 0 , 1 , 2 , . . . , Р - 1ý

образует поле Галуа или конечное поле порядка Р, т. е. поле состоящее из Р элементов с операциями сложения и умножения по модулю Р. Здесь Р называется характеристикой поля GF( P ).

Если Р = 2, то мы имеем наименьшее конечное поле с двумя элементами 0 и 1: GF(2) = í 0 , 1 ý, что и чаще всего является алфавитом для реальных дискретных и логических устройств. Приведём ещё один пример конечного поля GF( 5 ) = í 0 , 1 , 2 , 3 , 4 ý с соответствующими таблицами сложения и умножения ( вычитание и деление неявно определяются этими же таблицами ): + 0 1 2 3 4 * 1 2 3 4

0 0 1 2 3 4 1 1 2 3 4

1 1 2 3 4 0 2 2 4 1 3

2 2 3 4 0 1 3 3 1 4 2

3 3 4 0 1 2 4 4 3 2 1

4 4 0 1 2 3

Очевидно, для любого отрицательного целого числа х по модулю Р имеем х = Р + х ( mod P ), причём можно считать что - х меньше Р.

Так, например, если Р = 5, * - означает умножение, то 13 * 6 = 3 и 14*6 = 4, если * - деление, а - 3 = 2 по модулю 5.

Элемент a ¹ 0 поля GF( P ) называется примитивным элементом поля, если все его ненулевые элементы могут быть представлены в виде степени элемента a. Так, например, a = 2,3 являются примитивными для поля

GF( 5 ).

Арифметика конечных полей ничем не отличается от арифметики бесконечных полей ( например R,Q) за исключением того, что все операции в конечных полях GF( Р ) выполняются по модулю Р.

1.1.1. Составить таблицы сложения и умножения для поля GF( 7 ).

1.1.2. Определить противоположные и обратные элементы поля GF( 7 ).

1.1.3. Найти все примитивные элементы полей GF( 7 ) и GF( 13 ).

1.1.4. Доказать,что каждый ненулевой элемент поля GF(Р) имеет обратный элемент.

1.1.5. Определить число примитивных элементов поля GF( Р ).

1.1.6. Доказать, что для произвольных двух элементов

а, bÎGF( Р ) имеет место равенство ( а + b) ^Р = а ^Р+ b^Р.

1.1.7. Доказать, что ( Р - 1 )! = - 1.

1.1.8. Доказать, что если f ( x ) = a ₀ x ⁿ+ a ₁x ^{n - 1} + . . . + a _n ,a _nÎGF( Р ), то f ( х ^Р ) = ( f ( х ) ) ^Р .

1.1.9. Доказать, что корнями уравнения х^Р - х = 0 являются все элементы поля GF( Р ).

1.1.10. Найти число N_P ( a x + b ) всех линейных функций у = а х + b

в GF( Р ).

1.1.11. Найти число N_P (( a x + b ) / ( с х + d)) всех дробно - линейных функций у = (а х + b ) / ( с х + d ) в GF( Р ).

1.1.12. Определить число N_P ( a d - b c = k ) в GF( Р ) , где k Î GF( Р ).

1.1.13. Найти число решений N_P ( х ₁+ х ₂+ . . . + х _n= k ) уравнения

х ₁+ х ₂+ . . . + х _n= k в GF( Р ), где k Î GF( Р ).

1.1.14. Доказать, что х^Р - х =F₁( х ) F_Р ( х ), где F₁( х ) и F_Р ( х ) произведения всех простых над GF( Р ) полиномов степеней 1 и Р соответственно.

1.1.15. Определить число І_P(n)простых над GF( Р ) полиномов степени n. Доказать, что І_P(n)³ 1.

1.1.16. Разработать алгоритм построения простого над GF( Р ) полиномов заданной степени в явном виде.

1. 2. СОСТАВНОЕ ПОЛЕ ГАЛУА GF( Р ⁿ )

Пусть f ( x ) = x ⁿ + a₁ x^{n - 1}+ . . . +a _n - простой над полем GF( Р ) полином степени n (над каждым полем Галуа существует простой полином любой заданной степени ). Тогда

GF( Рⁿ ) = íb₀ x ^{n - 1}+ b₁ x ^{n - 2}+. . . +b _{n - 1}|b _iÎ GF( Р ) ý

образует поле Галуа или конечное поле порядка Рⁿ, т.е. поле, состоящее из Рⁿ элементов с операциями сложения и умножения по двойному модулю

f ( x ) и Р. Здесь Р также называется характеристикой поля GF( P ).

В данном построении поля Галуа GF( Рⁿ ) элементы поля представлены в виде полиномов над GF( P ) степени не выше n - 1 и

x ⁿ = ( Р - a₁ ) xⁿ^{- 1} + . . . + ( Р - a _n ).

Так, например, если Р = 2, f ( x ) = x ³ + х + 1, то элементы поля GF(2 ³ )

в полиномиальном представлении имеют вид b₀x²+ b₁x + b₂, где b _iÎGF( 2 ) и x ³= х + 1.

Полиномиальное Векторное Целочисленное Степенное

представление представление представление представление

0 0 0 0 0 0

1 0 0 1 1 х⁰

х 0 1 0 2 х ¹

х + 1 0 1 1 3 х ³

х ² 1 0 0 4 х ²

х ² + 1 1 0 1 5 х ⁶

х ²+ х 1 1 0 6 х ⁴

х ² + х + 1 1 1 1 7 х ⁵

Соответствующие таблицы сложения и умножения ( вычитание и деление неявно определяются этими же таблицами ) имеют вид:

+ 0 1 х х + 1 х ² х² + 1 х² + х х² + х +1

0 0 1 х х + 1 х² х² + 1 х² + х х² + х +1

1 1 0 х + 1 х х²+ 1 х² х² + х +1 х²+ х

х х х + 1 0 1 х² + х х² + х +1 х² х² + 1

х + 1 х + 1 х 1 0 х²+х +1 х² + х х²+ 1 х²

х ² х² х² + 1 х² + х х²+х+1 0 1 х х +1

х ²+ 1 х²+1 х² х²+х+1 х²+х 1 0 х+1 х

х ² +х х²+х х²+х+1 х² х²+1 х х+1 0 1

х² +х +1 х²+х+1 х²+х х²+1 х²х+1 х 1 0

* 1 х х + 1 х ² х² + 1 х² + х х² + х +1

1 1 х х + 1 х ² х² + 1 х² + х х² + х +1

х х х² х²+х х+1 1 х²+х+1 х²+1

х+1 х+1 х²+х х²+1 х²+х+1 х² 1 х

х² х² х+1 х²+х+1 х²+х х х²+1 1

х²+1 х²+1 1 х² х х²+х+1 х+1 х²+х

х²+х х²+х х²+х+1 1 х²+1 х+1 х х²

х²+х+1 х²+х+1 х²+1 х 1 х²+х х² х+1

Аналогично определяется примитивный элемент поля GF( Рⁿ ). При этом, полином, корнем которого является примитивный элемент поля

GF( Рⁿ ), называется примитивным полиномом. Так, например, для конечного поля GF( 2 ³ ) элемент х является примитивным элементом.

Пусть q = P ⁿ, где Р - простое, а n - произвольное натуральное число, тогда можно объединить приведённые два случая построения конечных полей в случай поля GF(q ).

1.2.1. Построить поле Галуа GF( 3²).

1.2.2. Построить таблицы сложения и умножения для полей GF(8) и GF(9).

1.2.3. Доказать, что для любых двух элементов a, bÎGF( q ) и любого натурального числа m = Р ^k имеет место равенство:

( a ± b )^m = a ^m ± b^m.

1.2.4. Доказать, что корнями уравнения х ^q - х = 0 являются все элементы поля GF( q ).

1.2.5. Определить число примитивных элементов поля GF( q ).

1.2.6. Доказать, что два поля Галуа с одним и тем же числом элементов изоморфны.

1.2.7. Доказать, что х ^q - х = П F _i ( x ), где F _i ( x ) - произведение всех

i|n

простых над GF( Р ) полиномов степени i.

1.2.8. Доказать, что над каждым полем GF( q ) существует примитивный полином любой положительной степени.

2. КОДИРОВАНИЕ ИНФОРМАЦИИ

Информация в широком смысле означает сведения, данные, сообщение, известие и т.д. Как правило, информацию можно представить в виде последовательностей символов или знаков некоторого алфавита. Это так называемый алфавит источника информации. Рассмотрим основные принципы кодирования информации для передачи, хранения и обработки в каналах связи.

2. 1. ОСНОВНЫЕ ПОНЯТИЯ. ПРИМЕРЫ КОДОВ

При кодировании информации, то есть при переходе от одного способа представления информации к другому, последовательности из символов источника по некоторому правилу отображаются в последовательности символов канала связи. Таким образом, кодом называется правило, описывающее однозначное соответствие (кодирование) символов алфавита источника символам (или словам) алфавита канала связи (помимо основного значения слова ”code”- ”кодекс”, ”свод законов”, начиная с середины XIX в. оно означало книгу, в которой словам естественного языка сопоставлены группы цифр или букв).

Пусть А = {a₁,a₂,...,a_m}, B={0,1,2,..,p-1}, p ³ 2 алфавиты источника сообщений и канала связи (в частности p=2) соответственно.Тогда общую схему передачи дискретной информации (СПДИ) можно представить в виде:

шум

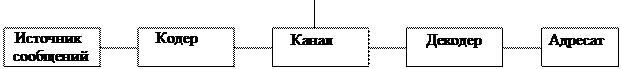u=u₁u₂ ...u_kx=x₁x₂...x_nx'= x₁'x₂'... x_l^'u=u₁u₂ ...u_k

Здесь u=u₁u₂ ...u_k - так называемое информационное слово, u_kÎA, x=x₁x₂...x_n- кодовое слово, x_nÎB, x '= x₁'x₂'... x_l^'- искажённое слово под воздействия шума (для простоты изложения предполагаем, что x_l¹Î B, хотя на практике возможно случай когда x_l¹Ï B, для конкретного или для всех l. Кодовое слово х иначе называют сигналом (изменение некоторой физической величины во времени, обеспечивающее передачу информации, называется сигналом, например, для радио сигналами являются электромагнитные колебания). В дальнейшем множество всех кодовых слов также назовём кодом.

Кодирование назовём побуквенным или блочным, если каждой букве или соответственно каждому блоку из А ставится в соответствие некоторое слово из букв В.

Основная задача теории кодирования заключается в оптимальном в некотором заранее заданном смысле (например, для защиты информации, для сжатия информации, для передачи информации с максимально возможной скоростью, для надёжного хранения информации и т.д.) передаче, хранении и обработки информации.

Кодирование называется р-ичным кодированием, если | В | = р. В данном разделе рассматриваются лишь двоичные кодирования, т.е. р=2,

В=í 0,1 ý. Приведём некоторые примеры.

1. Пусть А=í0 , 1 , 2 , 3 , . . .ý, В=í 0,1 ý. Рассмотрим кодирование С множества натуральных чисел, при котором числу i = 0 ставится в соответствие кодовое слово х = 0, а числу i ³ 1 - такое кодовое слово

х = х₁ х₂ . . . х_m, х_mÎí 0,1 ý, х₁ = 1,

что _m

å х _j2 ^{m - j} = k . ( 1 )

^{j = 1}

Так, например, числу i = 13соответствует кодовое слово х = 1101 длины m = 4.

Очевидно, данное кодирование С представляет собой перевод натуральных чисел в двоичную систему счисления и является примером неравномерного кодирования, так как кодовые слова имеют разные длины.

2. Рассмотрим пример равномерного кодирования С _k первых 2 ^k натуральных чисел.

Числу i=0 сопоставим кодовое слово у = 00...0 длины k, а каждому числу i ³ 1 - кодовое слово у = 0 ^{k - m} х ₁. . . х_m, где х ₁, . . . , х_m определяются соотношением ( 1 ).

Так, например, при k = 6 ( 0 £ i<2 ⁶ ) числу i =13 сопоставляется кодовое слово х=001101.

Данное кодирование С _k представляет собой перевод натуральных чисел в двоичную систему счисления с помощью k цифр и является примером равномерного кодирования, так как кодовые слова имеют равные длины.

3. Код С ₀ с проверкой на четность.

Каждому информационному слову u=u₁u ₂...u _k, u _kÎ í 0,1 ý сопоставим кодовое слово x=x ₁x ₂. . . x _{n ,}n = k +1, для которого

x _n = x ₁ + x ₂ + . . . + x _k, x _i=u _i , i = 1 , n ,

где + - сложение по модулю 2.

Так, например, при n=3 имеем следующие кодовые слова С ₀, все слова которого содержат чётное число единиц:

u ₁u ₂u ₃ x ₁x ₂x ₃x ₄

0 0 0 0 0 0 0

0 0 1 0 0 1 1

0 1 0 0 1 0 1

0 1 1 0 1 1 0

1 0 0 1 0 0 1

1 0 1 1 0 1 0

1 1 0 1 1 0 0

1 1 1 1 1 1 1

4. Код С ₁ с повторениями.

При данном способе кодирования сообщений информационный символ u_i повторяется n раз ( обычно n нечётно ).

Так, например, если u_iÎ í0,1ý, то код С ₁состоит всего лишь из двух кодовых слов длины n:

С ₁= í 0 0 . . . 0 , 1 1 . . . 1ý.

5. Код W_n Варшамова.

Пусть В = í 0 , 1 , . . . , р - 1ý - алфавит канала, a - произвольное целое число, n - длина кодового слова х = х₁х₂ . . .х_n , х_nÎ В.

Множество W_n всех слов х = х₁х₂ . . .х_n, для которых выполняется сравнение

W = å i x _i º a( mod n + 1),

_i _{= 1}

образует код Варшамова, т.е. _n

W_n = í х₁х₂ . . .х_n | W = å i x _i º a( mod n + 1), х_nÎ В ,a ÎZ ý.

^{i = 1}

Так, в частности, при р =3, n = 4, a = 0 из указанного сравнения получаем код W₄ , состоящих из 17 следующих кодовых слов:

0 0 0 0 1 1 1 1 0 2 1 2

1 0 0 1 2 1 2 0 0 2 2 0

0 1 1 0 0 0 2 1 2 2 2 2

1 2 0 0 2 0 0 2 2 1 1 2

2 0 1 0 0 1 0 2 1 2 2 1

2 2 0 1 1 0 2 2

Код W₄ является 3 -ичным равномерным нелинейным кодом.

6. Код М Морзе.

Для кода М алфавитом А сообщений служат буквы немецкого алфавита и десятичные цифры, а алфавитом канала является В = í . , _ , L ý, где L - пустой символ . Код М является примером побуквенного кодирования.

Так, например, букве А соответствует кодовое слово . _ , а цифре 6 - слово _ . . . . . и т.д. Код М также является неравномерным кодом. Если установить дополнительное соответствие

. 0 1,

_ 0 1 1,

L 0 0 0 ,

то код М можно рассматривать как двоичный неравномерный код.

Из приведённых выше примеров следует, что С _k, С ₀ , С ₁ ,W_n являются равномерными кодами, а С и М - неравномерными. Все они, кроме W_n, двоичные коды.

В процессе хранения ( передачи информации во времени ), передачи и обработки информации могут возникнуть ошибки ( искажение сигналов в каналах под воздействием шума ), и для того, чтобы уменьшить или исключить канальные ошибки вовсе, необходимо представить информацию в таком виде (т.е. выбрать подходящий способ кодирования ), чтобы она была устойчивой к различным канальным ошибкам. Коды, которые противостоят против канальных ошибок, называются помехоустойчивыми кодами.

Рассмотрим основные виды преобразований кодовых слов ( сигналов ), называемых канальными ошибками.

І . Симметричные ошибки. Это такие ошибки, при которых вероятности изменения каждого канального символа равны между собой. Тогда соответствующий канал называется симметричным каналом. Примером такого канала является двоичный симметричный канал ( ДСК ):

0 1 - р 0

р р

1 1 - р 1

Здесь с вероятностьюр ( 0 £ р £ 0.5) двоичный символ 0 переходит в двоичный символ 1:í 0 1ý, а символ 1 - в 0:í1 0 ý.Ошибки указанного типа í 0 1 , 1 0 ý иначе называют аддитивными ошибками или ошибками типа замещения.

Симметричные ошибки типов выпадения ( или стирания ) и вставки имеют соответственно вид:í0 L , 1 Lý , íL 0 , L 1ý , где L - пустой символ.

ІІ . Асимметричные ошибки. Это такие ошибки при которых вероятности изменения разных канальных символов не равны между собой. Тогда соответствующий канал называется асимметричным каналом.

Так, например, при асимметричной ошибке типа í 1 0 ý происходит замена 1 на 0 с некоторой вероятностьюр, но не наоборот. Такие ошибки возникают в результате размыканий в канале, ибо при размыкании сигнал может лишь исчезнуть.

Аналогично можно рассматривать асимметричные ошибки видов:

í 0 1ý , í1 0 ý , í0 L ý , í1 Lý , íL 0 ý , íL 1ý.

ІІІ . Арифметические ошибки вида + 2ⁱ ( -2ⁱ ). Это такие ошибки, при которых числовое значение искажённого сигнала на 2ⁱ больше ( соответственно меньше ) числового значения самого сигнала. Такие ошибки могут возникнуть при выполнении арифметических и логических операций, выполняемых в ЭВМ.

Таким образом, необходимо на основании характеристик канала выбрать такой способ кодирования, чтобы вероятность искажения передаваемого сообщения была бы меньше наперёд заданной величины.

2.1.1. Построить соответствующие 3-ичные коды, аналогично кодам С и С _k. _

2.1.2. Построить код С ₀ с проверкой на нечётность длины n.

2.1.3. Построить р - ичный код С ₁ с повторениями длины n.

2.1.4. Построить двоичный код Варшамова W₅.

2.1.5. Построить 3 - ичный код Морзе.

2.1.6. Разработать алгоритмы декодирования кодов С , С _k и W _n.

2.1.7. Определить мощность двоичного кода Варшамова W _n.

2. 2. ЛИНЕЙНЫЕ КОДЫ. СПОСОБЫ ИХ ЗАДАНИЯ

Пусть q = Рⁿ и GF( q ) - конечное поле в векторном представлении его элементов, а

GFⁿ( q ) = í х ₁ х ₂ . . . х _n | х _n ÎGF( P ) ý

- множество всех вектoров х = х ₁ х ₂ . . .х _nдлины n. Если х = х ₁х ₂ . . .х _n,

у = у ₁у ₂ . . . у _n ÎGF ⁿ(q), a Î GF( P ), то

х + у = ( х ₁ + у ₁)( х ₂ + у ₂ ) . . . (х _n + у _n )

a х = a х ₁a х ₂. . . a х _n

- сумма двух векторов ( слов ) и умножение на скаляр a соответственно ( здесь и далее все операции производятся по модулю Р ).

Расстоянием Хэмминга d ( х , у ) между двумя векторами х = х ₁х ₂. . .х _n

и у = у₁у₂ . . . у_n назовём число позиций, в которых они различаются.

Весом Хэмминга W ( х ) вектора х = х ₁ х ₂. . .х _n назовём число ненулевых компонент х _n .

Так, например, d ( 1 1 0 1 , 0 1 1 0 ) = 3 , W ( 1 1 1 0 ) = 3.

Очевидно, что d ( х , у ) = W ( х - у ) и d ( х , у ) удовлетворяет следующим условиям:

1. d ( х , у ) ³ причём d ( х , у ) = 0 при х = у;

2. d ( х , у ) = d ( у , х );

3. d ( х , у ) £ d ( х , z ) + d ( z , у ).

Таким образом, GFⁿ( q ) представляет собой метрическое пространство с метрикой d ( х , у ) Хэмминга.

Рассмотрим наиболее важные в практическом отношении случаи векторного пространства GFⁿ( 2 ) и двоичного симметричного канала. Последнее означает, что ошибки в ДСК могут быть лишь типа í 0 1 , 1 0ý.

Линейным [ n , k ] - кодом С_{[ n , k ]} назовём подпространство размерности k пространства GFⁿ( 2 ). Другими словами, линейный [ n , k ] - код представляет собой множество векторов длины n над GF(2), называемыми кодовыми словами, такое, что сумма двух произвольных кодовых слов также является кодовым словом, и произведение любого кодового слова на элемент поля GF(2) тоже является кодовым словом. Очевидно, в любом линейном коде нулевое слово 0 = 0 0 . . . 0 есть кодовое слово.

Так, например, если n = 3, то

С_{[ 3 , 2 ]} = í 0 0 0 , 0 1 1 , 1 0 1 , 1 1 0ý

- подпространство размерности 2 пространства

GF ³( 2 ) = í 0 0 0 , 0 0 1 , 0 1 0 ,0 1 1 , 1 0 0 , 1 0 1 , 1 1 0 , 1 1 1 ý ,

следовательно, С_{[ 3 , 2 ]} линейный [ 3 , 2 ] - код. В самом деле С_{[ 3 , 2 ]} образует пространство :

___+ 0 0 0 0 1 1 1 0 1 1 1 0

0 0 0 0 0 0 0 1 1 1 0 1 1 1 0

0 1 1 0 1 1 0 0 0 1 1 0 1 0 1

1 0 1 1 0 1 1 1 0 0 0 0 0 1 1

1 1 0 1 1 0 1 0 1 0 1 1 0 0 0 .

Теперь рассмотрим ещё один способ задания линейного кода.

Пусть u=u₁u₂ ...u_k- информационное слово, т.е. слово, которому соответствует один символ из алфавита А - источника передачи информации, x=x₁x₂...x_n - соответствующее переданное по ДСК кодовое слово ( или сигнал ), n ³ k , х ' = х ₁х₂ . . . х _i '. . . х_j'. . . х _n - принятое, в общем случае искажённое в позициях i, . . ., j слово.

Слово e = х - х ' = х + х ' = е ₁е ₂ . . . е _n - есть так называемое шумовое слово, для которого

ì 0 , если в i - й позиции нет ошибки;

е _i = í

î 1 , если в i - й позиции есть ошибка.

Итак, если е = 0 0 . . . 0, то х ' = х , т.е. переданное слово принято без ошибок, а при е ¹ 0 0 . . . 0 принятое слово х ' = х + е содержит ошибку. Таким образом, шум - это всего лишь некоторый двоичный вектор и такая трактовка вопроса передачи информации достаточно упрощает математическое описание обнаружения и исправления канальных ошибок в системах связи.

Для линейного способа кодирования информации применяется следующее общее правило: если u=u₁u₂ ...u_k- информационное слово, то для кодового слова x=x₁x₂... x_nсчитается, что

х_i = u _i , х _{k + i} = f _i ( х ₁ х ₂ . . . х _k ) , i = 1 , n - k , ( 2 )

где f _i ( х ₁ х ₂ . . . х _k ) , i = 1 , n - k - некоторые линейные функции. Соотношения (2) называются проверочными соотношениями.

Числоr = n - k называется числом проверочных, или избыточных, или же контрольных символов, а сами символы х _{k + 1 ,}. . . , х _n- проверочными, или избыточными, или же контрольными символами. Таким образом, для построения линейных помехоустойчивых кодов приходится внести r дополнительных символов в кодовые слова и тем самым уменьшить скорость передачи информации R =k / n , где k - число информационных символов, n - длина кодового слова.

Пусть

f _i ( х ₁ х ₂ . . . х _к ) = h _{i 1}* x ₁ + h _{i 2}* x ₂+ . . . + h _i _k* x _k , i = 1 , r ,

где h _{i k} ÎGF( 2 ).Тогда из проверочных соотношений ( 2 ) имеем :

h _{i 1}* x ₁ + h _{i 2}* x ₂+ . . . + h _{i k}* x_k+ x_{k +} _i = 0 , i = 1 , r . ( 3 )

Матрица H = ( h _{i j} )_rⁿ размерности ( r xn) из коэффициентов (3 ) - так называемая проверочная матрица и имеет вид:

h_{1 1} h_{1 2} . . . h_{1 k}1 0 . . . 0 0

h _{2 1}h _{2 2} . . . h _{2 k}0 1 . . . 0 0

H = . . . = ( A | E _r),

h_{r 1}h _{r 2} . . . h _{r k} 0 0 . . . 0 1

где A- двоичная матрица размерности (r ´ k), а E _r - единичная матрица размерности ( r ´ r). Её применяют на практике для декодирования информации.

Линейным [ n , k ] - кодом с проверочной матрицей H назовём множество всех двоичных слов x=x ₁x ₂. . . x _n таких, что H х ^т = 0 т.е.

С_{[ n , k ]} = í х | H х ^т = 0 ý .

Итак, мы имеем более простой способ задания линейного С_{[ n , k ]} кода с помощью проверочной матрицы. Данный способ задания линейного кода зависит только от проверочной матрицы.

Так, например, пусть при n = 6 , к = 3 и r = 3

х ₄ = х ₁ + х ₂ , х ₁+ х ₂ + х ₄ = 0 ,

х ₅= х ₁ + х ₃, или х ₁ + х₃ + х₅ = 0 ,

х ₆ = х ₂ + х₃ , х ₂+ х₃+ х₆ = 0 .

Тогда проверочная матрица H линейного [ 6 , 3 ] - кода С_{[ 6 , 3 ]} имеет вид:

1 1 0 1 0 0

H = 1 0 1 0 1 0 ,

0 1 1 0 0 1

а все его кодовые слова можно найти из указанных выше проверочных соотношений следующим образом в виде кодовой книги:

u₁u₂u₃ х₁х₂х₃ х₄х₅х₆

0 0 0 0 0 0 0 0 0

0 0 1 0 0 1 0 1 1

0 1 0 0 1 0 1 0 1

0 1 1 0 1 1 1 1 0

1 0 0 1 0 0 1 1 0

1 0 1 1 0 1 1 0 1

1 1 0 1 1 0 0 1 1

1 1 1 1 1 1 0 0 0

или как С_{[ 6 , 3 ]}= í х | H х ^т = 0 ý .

Таким образом,

С_{[ 6 , 3 ]}=í000000,001011,010101,011110,100110,101101,110011,111000 ý.

Очевидно, если некоторое слово х = х₁х₂х₃ х₄х₅х₆ Î С_{[ 6 , 3 ]} , то H х ^т = 0,

в противном случае H х ^т ¹ 0.

Рассмотрим ещё один способ задания линейного кода - с помощью порождающей матрицы.

Пусть С линейный [ n , k ] - код, т.е. подпространство размерности k

пространства GFⁿ( 2 ). Тогда в этом подпространстве С существует базис b₁ ,b ₂ , . . . b _k , с помощью которого можно получить все кодовые слова линейного кода С.

Матрица G размерности ( k ´ n), строками которой являются базисные векторы b₁ ,b ₂ , . . . b _k, называется порождающей матрицей линейного кода С. Говорят также, что код С представляет собой пространство строк порождающей матрицы G.

Другими словами, если u=u₁u₂ ...u_k- информационное слово, то х = u G - кодовое слово.

Можно доказать,что если проверочная матрица H линейного [ n , k ]- кода С имеет вид ( A | E _r), то порождающая матрица этого же кода представляется в виде G = (E _к | - А _к^т ) ( в двоичном случае - А = А ).

Так, например, для линейного кода С_{[ 6 , 3 ]} порождающая матрица G имеет вид :

1 0 0 1 1 0

G= 0 1 0 1 0 1 ,

0 0 1 0 1 1

а базисные векторы - b₁ = 1 0 0 1 1 0 , b ₂ = 0 1 0 1 0 1, b₃ = 0 0 1 0 1 1.

Для определения кодового слова соответствующему, например, информационному слову u = 1 0 0 , имеем:

1 0 0 1 1 0

х= u G = ( 1 0 0 ) 0 1 0 1 0 1 = 1 0 0 1 10 ,

0 0 1 0 1 1

что в самом деле принадлежит коду С_{[ 6 , 3 ]} .

Таким образом, мы описали ещё один способ задания линейного [n, k ]- кода с помощью порождающей матрицы, что применяется на практике при кодировании информации линейными кодами.

2.2.1. Пусть х = х ₁х ₂ . . .х _n, у = у ₁у ₂ . . . у _n ÎGF(2ⁿ ). Установить связь между расстояниями Хэмминга d _Х( х , у ) и Евклида d _Е ( х , у ) .

2.2.2. Доказать, что для расстояния Хэмминга выполняется неравентво треугольника d ( х , у ) £ d ( х , z ) + d ( z , у ).

2.2.3. Найти все подпространства пространства GF³(2 ).

2.2.4. Доказать, что H х' ^т = 0 тогда и только тогда, когда шумовое слово равно нулю.

2.2.5. Построить пример нелинейного кодирования.

2.2.6. Для фиксированной длины n определить наименьшее число избыточных символов.

2.2.7. Определить скорости передачи информации для кодов: С , С ₀, С₁, С_k , С_{[ 6 , 3 ]} , М , W _n .

2.2.8. Как иначе можно задать проверочную матрицу H ?

2.2.9. Построить все линейные коды длины не более семи .

2.2.10. Построить проверочную матрицу кодов С ₀, С ₁.

2.2.11. Доказать, что если H = ( A | E _r) , то G = (E _к | - А _к^т ).

2.2.12. Найти все базисы линейного С_{[ 6 , 3 ]} - кода.

2.2.13. Построить троичный линейный код длины 13.

2.2.14. Доказать, что G H ^т = 0 .

2.2.15. Построить проверочную и порождающую матрицы для линейно- го [ n , n - 1] - кода.

2.2.16. Доказать, что d ( х , у ) = d ( х + z , у + z ) = W ( х + у ).

2.2.17. Пусть W ( х ) = W ( у ) = w . Доказать, что d ( х , у ) - чётное число .

2.2.18. Для векторов х и у определим их произведение:

х * у = х₁ у_{1 ,} х ₂у ₂ , . . . , х_n у _n.

Показать, что тогда W ( х + у ) = W ( х ) + W ( у ) - 2 W ( х * у ) .

2.2.19. Разработать алгоритм декодирования линейных блочных кодов.

2. 3. СВОЙСТВА ЛИНЕЙНОГО КОДА. КОДЫ ХЭММИНГА

Пусть С линейный [ n , k ] - код с проверочной матрицей H размерности

( n - k ) ´ n . Если все строки матрицы H линейно независимы , то число кодовых слов ( т .е . мощность кода ) равно ½ В ½^k , где В - алфавит канала. Далее, если х , у Î С и aÎ В , то х + у , a х также принадлежат линейному коду С, так как

H ( х + у )^т = H х^т + H у^т = 0 , H (aх )^т = a Hх^т = 0 .

Обозначим через d _С минимальное расстояние линейного кода С, т.е.

d _С= min í d ( х , у ) ½ х , у Î С , х ¹ у ý .

Линейный код С длины n, размерности k и с минимальным расстоянием d _С ( или же с кодовым расстоянием d _С = d ) назовём также линейным

[ n , k , d ] - кодом.

Рассмотрим простой способ нахождения минимального расстояния линейного двоичного кода, а именно, кодовое расстояние линейного двоичного кода равно минимальному весу ненулевых кодовых слов, т.е.

d _С= min í W ( х ) ½ х Î С , х ¹ 0 ý ,

так как

d _С= min í d ( х , у )½х , у Î С , х ¹ у ý = min í W ( х + у )½ х , у Î С, х¹у ý=

= min í W (z )½ z Î С, z ¹0 ý .

Код с кодовым расстоянием d может исправлять [(d - 1 ) / 2 ] ошибок. Если d чётное, то код может одновременно исправлять (d - 1 ) / 2 ошибок и обнаруживать d / 2 ошибок. Таким образом, для построения оптимальных кодов необходимо учитывать его эффективность, т.е. скорость передачи информации и максимальность кодового расстояния для заданных параметров n и k.

Так, например, для кода С ₀ с проверкой на чётность R = k / ( k + 1 ), а d _С= 2 , т.е. его скорость высокая, а корректирующая возможность очень низкая, он обнаруживает всего лишь одну ошибку. И наоборот, для кода С₁ с повторениями R = 1 / n , а d _С= n , т.е. он достаточно высокой корректирующей возможностью, но с низкой скоростью.

Для построения линейного [ n , k , d ] - кода длины n размерности k с заданным расстоянием d и с проверочной матрицей H необходимо и достаточно, чтобы любые d - 1 столбцов матрицы H были линейно независимы и в то же время нашлись бы d линейно зависимых столбцов. Причём, если С - [ n , k , d ] - код, то n - k ³ d - 1 , т.е. d £ n - k + 1 ( Граница Синглтона ) и указанные выше свойства справедливы для линейных кодов над любым конечным полем.

А для обнаружения и исправления ошибок в каналах связи необходимо воспользоваться равенством:

S = H x ^'^т = å e_i H_i = H _a + H_b + . . . + H_c ,

где H_i - i - й столбец матрицы H , i - номер ошибочной позиции принятого слова x ^' , так как если x ^' = х + e , то S = H x ^{' т} = H ( x + e ) ^т = H e ^т.

Слово S ^т называется синдромом принятого слова x ^'.

Теперь рассмотрим класс двоичных линейных кодов , которые обнаруживают и исправляют одну симметрическую ошибку.

Двоичный код Хэмминга H _r. Для любого r ³ 2 двоичный код Хэмминга H _r длины n = 2 ^r - 1 имеет проверочную матрицу H _r , столбцы которой состоят из всех ненулевых двоичных векторов длины r, причём каждый вектор встречается в матрице H один раз, т.е.

0 0 . . . 1 1

H _r = . . . = 1 , 2 , . . . , 2 ^r - 1 .

0 1 . . . 1 1

1 0 . . . 0 1

Кодовое расстояние кода H _r равно 3 , так как любые два столбца её проверочной матрицы H _r линейно независимы, и существуют 3 линейно зависимых столбца, следовательно, код Хэмминга обнаруживает и исправляет одну симметрическую ошибку. Данный код представляет собой линейный [2 ^r - 1 , 2 ^r - r - 1 , 3 ] - код.

В случае, когда длина кода Хэмминга не равна 2 ^r - 1 , то r определяется как наименьшее целое решения неравенства

n < 2 ^r - 1 ,

а проверочная матрица H _r^' соответствующего кода Хэмминга длины n<2 ^r-1

получается из проверочной матрицы H _r путём исключения любых её 2 ^r-1- - n столбцов.

Так, например, двоичный [7 , 4 , 3 ] - код Хэмминга имеет следующую проверочную матрицу:

0 0 0 1 1 1 1

H₃ = 0 1 1 0 0 1 1 = [ 1 , 2 , 3 , 4 , 5 , 6 , 7 ] ,

1 0 1 0 1 0 1

а [6 , 3 , 3 ] - код - матрицу ( из H ₃ исключим, например, последний столбец ):

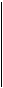
0 0 0 1 1 1

H₃^' = 0 1 1 0 0 1 = [ 1 , 2 , 3 , 4 , 5 , 6 ] .

1 0 1 0 1 0

Приведём способ построения новых кодов из заданных на примере кодов Хэмминга и кодов проверки на чётность в результате чего кодовое расстояние и длина нового кода увеличиваются на единицу. Это так называемый расширенный [n + 1 , n - r , 4 ] - код Хэмминга с проверочной матрицей:

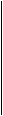
1 1 . . . 1

H _{r + 1} = .

H _r . .

Два кода называются эквивалентными, если они отличаются только перестановкой символов в кодовых словах. Так, например, коды

А₁= í0 0 0 0, 0 0 1 1, 1 1 0 0, 1 1 1 1ý , А₂= í0 0 0 0, 0 1 0 1, 1 0 1 0, 1 1 1 1ý

являются эквивалентными [ 4 , 2 , 2 ] - кодами.

Если В(n , d) - максимальная мощность некоторого линейного [n, k, d ]-

- кода длины n с кодовым расстоянием d, то для кодов Хэмминга она определяется формулой ₂^r_{- r - 1}

В(n , 3 ) = 2 ,

а его эффективность, т.е. его скорость передачи информации - формулой:

R = (2^r - r - 1 ) / (2^r - 1) .

2.3.1. Доказать, что код с кодовым расстоянием d может исправлять

[(d - 1 ) / 2 ] ошибок, причём если d чётное, то он может одновременно исправлять (d - 1 ) / 2 ошибок и обнаруживать d / 2 ошибок.

2.3.2. Доказать, что если H - проверочная матрица линейного кода длины n , то код имеет минимальное расстояние d тогда и только тогда, когда любые d - 1 столбцов матрицы H линейно независимы, но найдутся d линейно зависимых столбцов.

2.3.3. Доказать, что если i , j , . . . , k - номера ошибочных позиций принятого слова x ' некоторого линейного кода с проверочной матрицей H, то S = H x '= H _i+ H _j + . . . + H _k , где H _i - i- й столбец матрицы H.

2.3.4. Доказать, что кодовое расстояние кодов Хэмминга равно 3 .

2.3.5. Доказать, что кодовое расстояние расширенных кодов Хэмминга равно 4 .

2.3.6. Выписать все кодовые слова кода H ₃ .

2.3.7. Построить проверочную матрицу [13 , 10 , 3 ] - кода Хэмминга над полем GF( 3 ).

2.3.8. Доказать, что если С - двоичный линейный код и слово а Ï С , то

С U ( а + С ) также является двоичным линейным кодом.

2.3.9. Доказать, что если С является [n , k , d ]- кодом над полем GF( Р ),

то множество всех слов GFⁿ( Р ) можно разбить на непересекающиеся смежные классы : GF ⁿ ( Р ) = С U ( а₁ + С ) U ( а ₂ + С ) U . . . U ( а _t + С ) , где t = P ⁿ^{- k} - 1 .

2.3.10. Доказать, что коды С и а + С являются эквивалентными для любого слова а.

2.3.11. Построить порождающую матрицу кода H _r и, используя её, показать, что каждое ненулевое кодовое слово имеет вес не менее 3 .

2.3.12. Доказать, что код Хэмминга является совершенным кодом ( код называется совершенным, если он покрывает всё пространство ).

2.3.13. Доказать, что если С - [n , k , d ]- код , то d £ n - k + 1 ( Граница Синглтона ).

2.3.14. Определить значение величины В( n , d ) для любого линейного кода.

2.3.15. Разработать алгоритмы кодирования и декодирования для линейных [n , k , d ]- кодов.

2.3.16. Разработать алгоритмы кодирования и декодирования для линейных кодов Хэмминга.

2.3.17. Доказать, что код Хэмминга обнаруживает и исправляет одну симметрическую ошибку на примере H ₃.

2.3.18. Определить веса всех кодовых слов (спектр весов) кода H _r .

2. 4. ЦИКЛИЧЕСКИЕ КОДЫ

Важнейшим частным случаем линейных кодов являются циклические коды, которые допускают простую техническую реализацию и могут быть использованы для изучения, поиска и построения других не менее эффективных в практическом отношение кодов.

Линейный код С называется циклическим, если любой циклический сдвиг кодового слова также является кодовым словом , т.е. если с₀с₁. . . с_{n -1}

принадлежит С, то и с_{n -1}с₀ . . . с_{n -2}принадлежит С.

Для описания циклических кодов сопоставим каждому кодовому слову с₀с₁. . . с_{n -1} Î GF ⁿ ( P ) полином степени n -1 :

с ( х ) = с₀+ с₁х + . . . + с_{n -1}х ^{n -1} .

Тогда сумме двух кодовых слов будет соответствовать полином, представляющий сумму соответствующих им поиномов ( все вычисления здесь и ниже по модулю Р ). Причём сумма полиномов равна полиному, соответствующему некоторому кодовому слову. Однако произведение полиномов, каждый из которых имеет степень не больше n - 1, в общем случае не соответствует кодовому слову длины n, так как его степень может быть больше n - 1.

Так, например, код

С =í0 0 0 , 0 1 1 , 1 0 1 , 1 1 0ý

является циклическим кодом длины 3 и его кодовым словам соответствуют полиномы:

0 , х + х ² , 1 + х ² , 1 + х .

Сумме кодовых слов 1 0 1 и 1 1 0 соответствует слово 0 1 1 , которому соответствует полином с ( х ) = х + х ² , а произведению этих же слов не соответствует кодовое слово. Поэтому нам необходимо такое представление произведения полиномов, а именно по модулю полинома х ⁿ - 1, при котором результату будет соответствовать также полином степени не больше

n - 1.

В самом деле, если кодовому слову с₀с₁. . . с_{n -1} соответствует полином

с ( х ) = с₀+ с₁х + . . . + с_{n -1}х ^{n -1},

то циклическому сдвигу с_{n -1}с₀ . . . с_{n -2} будет соответствовать полином

х с ( х ) = с₀х + с₁х ² + . . . + с_{n -1}х ⁿ = с _{n -1}+ с ₀х + с₁х ²+ . . .

+ с_{n -2}х ^{n -1}+ с_{n -1} ( х ⁿ-1) = с_{n -1}+ с ₀х + . . . + с _{n -2} х ^{n -1}

по модулю х ⁿ -1 .

Таким образом, умножению полинома с ( х ) на х соответствует циклическому сдвигу кодового слова.

Приведём практический способ построения циклического кода с помощью так называемого порождающего полинома.

Пусть

g ( x ) = g₀ + g₁ x + . . . + g_r x^r

некоторый делитель полинома х ⁿ - 1 степени r ³ 1 - порождающий полином циклического кода длины n. Рассмотрим множество всех полиномов f(x) степени не выше n - 1 которые делятся на g( x ), т.е. множество полиномов с ( х ) = f ( x ) g ( x ). Каждому такому полиному

с ( x ) = с₀+ с₁х + . . . + с_{n -1}х ^{n -1}

сопоставим слово его коэффициентов с₀с₁. . . с_n-1 и обозначим через С множество всех таких слов.

Покажем, что С является циклическим кодом длины n размерности n - r с порождающим полиномом g ( x ), причём сообщение f ( x ) кодируется словом с ( х ) = f ( x ) g ( x ).

Пусть с₀с₁. . . с_{n - 1} и d₀d₁ . . . d_{n - 1} - два произвольных слова из С, которым соответствуют полиномы

с ₁( x ) = с₀+ с₁х + . . . + с_{n -1}х ^{n -1} = f ₁( x ) g ( x )

с ₂( х ) = d₀+ d₁ х + . . . + d_{n - 1} х^{n -1} = f ₂( x ) g ( x ) .

Тогда полином

с ₁( x )+с ₂( х ) = ( с₀+d₀ ) + ( с₁+d₁)х + . . . + ( с_{n -1}+d_{n - 1} )х^{n -1}=

= g ( x ) (f ₁( x )+f ₂( x )),

которому соответствует слово (с₀+d₀) (с₁+d₁). . .(с_{n -1}+d_{n - 1}), также делится на g(x) и, следовательно,( с₀+d₀ )( с₁+d₁). . .( с_{n -1}+d_n-1) принадлежит С, т.е. С - линейный код.

Далее, если с₀с₁. . . с_{n - 1} Î С, то его циклический сдвиг с_{n -1}с₀ . . . с_{n -2} также принадлежит С, в чём легко убедиться.

Так, например, полином g ( x ) = 1 + х + х ³ над GF(2) порождает циклический код длины 7 с минимальным расстоянием 3, что представляет собой двоичный [7 , 4 , 3 ] - код Хэмминга.

Если

g ( x ) = g₀ + g₁ x + . . . + g_r x^r

порождающий полином циклического кода С, то матрица

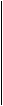g₀ g₁ . . . g_r 0 . . . 0 g(x) 0 . . . 0

0 g₀ g₁ . . . g_r 0 . . . 0 0 хg(x) 0 . . . 0

G = . . . = . . .

0 . . .0 g₀ g₁ . . . g_r 0 . . . 0х^{n - r - 1} g(x)

представляет собой порождающую матрицу циклического кода С, так как С - пространство строк матрицы G.

С другой стороны, для декодирования циклического кода С, определим проверочный полином и проверочную матрицу соответственно как:

h( x ) = (x ⁿ - 1) / g( x ) = h₀ + h ₁x + . . . + h _kx ^k , h _k ¹ 0 , h _kÎ GF(P) ,

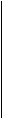
0 0 . . . 0 h_k . . . h ₂ h ₁ h ₀ 0 0. . .0 h(x)

H = 0 h_k . . . h ₂ h ₁ h ₀ 0 0 хh(x) 0

. . . = . . .

h_k . . . h ₂ h ₁ h ₀ 0 0 . . . 0 х ^{n - k - 1} h(x) 0 0 . . .0

Таким образом, мы имеем основные способы задания циклических кодов.

Ранее рассмотренные коды Хэмминга H _r в самом деле суть циклические коды с порождающими полиномами g ( x ) равными примитивным полиномам полей Галуа. А для определения всех порождающих полиномов, в общем случае, необходимо иметь разложение полинома x ⁿ - 1 на простые множители над полем Галуа, что является особым вопросом исследования. Так, например,если

x ⁿ - 1 = g ₁( x ) g ₂( x ) . . . g _m( x ),

над GF(q), то можно получить 2^m различных порождающих полиномов

g( x ) и столько же циклических кодов.

2.4.1. Найти все делители полинома х ⁷ - 1 над GF(2).

2.4.2. Нормированный полином М( х ) с коэффициентами из GF(Р) наименьшей степени, для которого М_a(a) = 0 , a Î GF(q) называется минимальным полиномом элемента a. Доказать, что:

а ) М_a( х ) неприводим над GF(Р);

б ) степень минимального полинома примитивного элемента поля

GF(q) равна n ( такой полином называется примитивным );

в ) М_a( х ) = М_a^р( х ).

2.4.3. Найти все примитивные полиномы заданной степени поля GF(Р).

2.4.4. Определить порождающий полином циклического[ 15 , 11 , 3 ]- кода Хэмминга H ₄.

2.4.5. Разработать алгоритмы кодирования и декодирования циклических кодов.

2.4.6. Доказать, что если h ( x ) делится на х^Т - 1, то минимальное расстояние не может быть больше чем n / Т.

2.4.7. Код С называется реверсивным, если для произвольного слова

с₀с₁. . . с_{n -1} Î С следует, что с_{n -1} . . .с₁с₀ Î С. Доказать, что циклический код реверсивен тогда и только тогда, когда все элементы, обратные корням его порождающего полинома, также являются корнями порождающего полинома.

2.4.8. Доказать, если - 1 равна некоторой степени q по модулю n, то каждый циклический код над GF(q) длины n реверсивен.

2.4.9. Доказать, что x ⁿ - 1 имеет n различных корней над GF(q).

2.4.10. Циклотомический класс С_s по модулю n над GF(q) определяется как множество:

С_s = { s , sq ,sq², . . . , sq^m_s^{- 1} } ,

где sq^m_sº s (mod n ) , ( q , n ) = 1. Доказать, что

х ⁿ- 1 = П М _s ( х ) ,

где s пробегает всё множество представителей по модулю n.

2.4.11. Определить проверочный полином для кода Хэмминга H₃ .

2.4.12. Доказать, что код Хэмминга H_r является циклическим кодом с порождающим полиномом g (x)=М_a (х), где a- примитивный элемент поля GF(q).

2.4.13. Построить наименьший циклический код, содержащее слово

0 0 1 1 0 1 0.

2.4.14. Разработать алгоритм разложения полинома х ⁿ- 1 над GF(q).

2.4.15.Определить минимальное расстояние циклического кода длины n.

КОДЫ БЧХ, ИСПРАВЛЯЮЩИЕ ДВЕ ОШИБКИ

Рассмотримкласс двоичных циклических кодов, которые обнаруживают и исправляют любые t - кратные ошибки. Это так называемые коды Боуза-Чоудхури-Хоквингема ( или, кратко, коды БЧХ ).

Здесь опишем обобщение кодов Хэмминга, позволяющее исправлять две ошибки с помощью проверочной матрицы H_r кода Хэмминга H_r .

Пусть n = 2^r - 1 - длина кода Хэмминга, r - число проверочных символов кодовых слов H_r ,

H_r = [ 1 , 2 , 3 ,..., 2^r - 1]

- проверочная матрица размерности ( r ´ 2^r - 1 ) кода H_r.

Построим проверочную матрицу H_r' обобщённого кода Хэмминга, исправляющего две ошибки, путём добавления ещё r строк к проверочной матрице H_r кода Хэмминга следующим образом:

1 2 3 . . . 2^r - 1

H_r' = f(1) f(2) f(3) . . . f(2^r - 1) ,

где f(i) - некоторая функция, отображающая r - мерные вектора в r - мерные вектора.

Допустим, что произошли две ошибки - на позициях i и j. Нам необходимо выбрать функцию f(i) так, чтобы декодер по синдрому S принятого слова x' мог найти i и j.

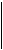
Так как i + j к ₁

S = H'x'^T = H_i' + H'_j = f(i) + f(j) = к ₂ ,

то для обнаружения двух ошибок необходимо декодеру решить систему уравнений:

ì i + j = к ₁ ,

î f(i) + f(j) = к ₂ .

Можно проверить, что при выборе функции f(i) = i³ система имеет ровно два решения i и j.

В самом деле при f(i) = i ³ имеем: ì i + j = k ₁ ,

î i³ + j³ = k ₂ ,

откуда при к ₁ ¹ 0 находим, что

ì i + j = k ₁ ,

î i * j = k²₁ + к ₂ / к ₁ ,

т.е. i и j являются корнями уравнения

Z ² + k ₁ Z + k²₁ + к ₂ / к ₁ = 0.

Таким образом, проверочная матрица H_r' искомого кода принимает вид:

1 2 3 . . . 2^r - 1

H_r' = 1 ³ 2 ³ 3 ³ . . . (2^r - 1) ³ ,

а его параметры - n = 2^r - 1 , k = n - 2 r , d = 5.

Заметим, что для операций над r - мерными векторами удобно интерпретировать каждый двоичный вектор как некоторый двоичный полином степени не больше r - 1, а сами операции выполнять над соответствующими полиномами по модулю неприводимого над GF(2) полинома М(х) степени r. Тогда результат любой операции будет полином степени не выше r - 1, и которому будет соответствовать r - мерный вектор.

В частности, при r = 3, М( х ) = х ³ + х + 1 двоичный код БЧХ длины 7, исправляющий две ошибки, имеет проверочную матрицу:

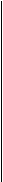
0 0 0 1 1 1 1

0 1 1 0 0 1 1

1 0 1 0 1 0 1

H_r' = 0 0 1 1 1 1 0

0 1 0 0 1 1 1

1 1 0 1 0 1 0

Здесь

a ₀ a ₁ a ₂ a ₀х ² + a ₁х + a ₂ ,

т.е. каждому 3 -мерному вектору сопоставлен полином 3-й степени и все операции выполнены по модулю М( х ) = х ³ + х + 1 в поле GF(2).

На практике для построения проверочной матрицы H_r' кода БЧХ необходимо воспользоваться степенными представлениями элементов полей Галуа. Так, например, проверочной матрице H₃ кода H₃ соответствует матрица

H₃ = [ 1 a a ² a ³ a ⁴ a ⁵ a ⁶ ] ,

а проверочной матрице H₃' кода БЧХ -

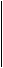
1 a a ² a ³ a ⁴ a ⁵ a ⁶

H₃' = ,

1 a³ a ⁶ a ² a ⁵ a a ⁴

где a Î GF(2 ³) - корень уравнения a ³ + a + 1 = 0.

В общем случае можно доказать, что таким образом построенный код

БЧХ является циклическим кодом с порождающим полиномом

g ( x ) = М _a ( х ) М _a ³( х ) ,

где М _a ( х ) и М _a ³( х ) - минимальные полиномы элементов a и a ³ соответственно.

2.5.1. Найти степенные представления элементов поля GF(2 ⁴) и построить соответствующую проверочную матрицу кода БЧХ.

2.5.2. Определить все примитивные полиномы поля GF(2 ⁴).

2.5.3. Разработать алгоритм декодирования кодов БЧХ.

2.5.4. Доказать, что коды БЧХ являются циклическими кодами.

2.5.5. Доказать, что код БЧХ с порождающим полиномом

g ( x ) = М _a ( х ) М _a ³( х ) имеет кодовое расстояние равное 5.

2.5.6. Найти все корни полинома g ( x ) = М _a ( х ) М _a ³( х ).

2.5.7. Построить троичный код БЧХ, исправляющий две ошибки.

2.5.8. Построить двоичный код БЧХ, исправляющий более двух ошибок.

2.5.9. Определить кодовое расстояние циклического кода по порождающему полиному g ( x ).

2.5.10. Пусть g (x) имеет d корней a , a² , . . . , a^{d - 1}. Установить связь между d и минимальным расстоянием кода БЧХ с порождающим полиномом g ( x ).

2. 6. НЕЛИНЕЙНЫЕ КОДЫ. КОДЫ АДАМАРА

Для каждого линейного кода С и произвольных двух его кодовых слов х , у сумма х + у также кодовое слово, что не всегда выполняется для нелинейных кодов, хотя в большинстве случаев нелинейные коды более эффективные , чем соответствующие линейные коды .

Назовём ( n , M , d ) - кодом множество из М слов длины n ( в алфавите GF(q), в частности здесь рассмотрим алфавит GF(2) ) такое, что для любых двух слов х ¹ у d(х , у) ³ d и d является наибольшим числом с таким свойством.

Из данного определения следует, что двоичный линейный [ n , k ,d ] - код является ( n , 2 ^k, d ) - кодом ( круглые скобки используются для кода, который может быть или не быть линейным ).

Будем говорить, что два ( n , M , d ) - кода эквивалентны, если один может быть получен из другого перестановкой n символов и добавлением фиксированного слова.

Скорость передачи для нелинейного кода определяется как

R = log _q M / n ,

что сводится к равенству

R = к / n ,

если код линеен.

Многие нелинейные коды строятся с помощью матриц Адамара. Это матрица H _n размерности n ´ n из элементов ± 1, такая, что

H _n H^Т_n= n Е ,

где Е -единичная матрица размерности n ´ n . Другими словами, скалярное произведение произвольных двух различных строк H _n в поле действительных чисел равно нулю. Так, например,

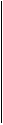1 1 1 1

1 -1 1 -1

H ₄= 1 1 -1 -1 .

1 -1 -1 1

Матрица Адамара H _n называется нормализованной матрицей, если её первый столбец и первая строка состоят из одних единиц ( как в матрице H ₄). Если существует матрица Адамара H _n порядка n, то n равно 1 или 2 или делится на 4 (наименьший порядок, для которого матрица Адамара ещё не построена равен 268 на 1977 г.).

Для построения матриц Адамара можно воспользоваться следующим способом. Пусть H _n и H _m - две матрицы Адамара порядков n и m соответственно. Тогда существует матрица Адамара H _nmпорядка nm, для чего необходимо каждый элемент матрицы H _n заменить матрицей H _m, умноженная на этот элемент. Так, например, из матрицы

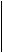1 1

H₂ = 1 -1

можно получить матрицу H ₄, а из H ₄- матрицу Адамара H ₈:

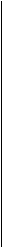
1 1 1 1 1 1 1 1

1 -1 1 -1 1 -1 1 -1

1 1 -1 -1 1 1 -1 -1

1 -1 -1 1 1 -1 -1 1

H ₈= 1 1 1 1 -1 -1 -1 -1 .

1 -1 1 -1 -1 1 -1 1

1 1 -1 -1 -1 -1 1 1

1 -1 -1 1 -1 1 1 -1

Эти матрицы Адамара называются матрицами Сильвестра.

Назовём две матрицы Адамара эквивалентными, если одна может быть получена из другой перестановками строк и столбцов и умножением строк и столбцов на - 1.

Теперь перейдём к рассмотрению кодов Адамара.

Пусть H _n - нормализованная матрица Адамара порядка n. Если все элементы +1 заменить на 0, а элементы - 1 заменить на 1, то H _nпревратится в двоичную матрицу Адамара А_n. Так как строки H _nортогональны, то любые две строки матрицы А_n совпадают в n / 2 позициях и различаются в n / 2 позициях, и поэтому расстояние Хэмминга между ними равно n / 2.

Матрица А_n позволяет построить следующие три кода Адамара:

I. ( n - 1, n , n / 2 ) - код А_n, состоящий из строк матрицы А _nс выкинутым первым столбцом ( этот столбец состоит из одних нулей ).

Так, например, при n = 4 имеем:

А₄= í0 0 0 , 1 0 1 , 0 1 1 , 1 1 0 ý.

II. ( n - 1 , 2 n , n / 2 ) - код В₄ , состоящий из слов кода А _n и их дополнений.

При n = 4 имеем:

В₄ = í 000 , 101 , 011 , 110 , 111 , 010 , 100 , 001 ý.

III. ( n , 2- n , n / 2 ) код С_n , состоящий из строк матрицы А _n и их дополнений.

При n = 4 имеем:

С₄= í0000, 0101, 0011, 0110, 1111, 1010, 1100, 1001 ý.

В частности, если n = 2 ^r, то все три кода Адамара А_n , В_n и С_n являются линейными. В остальных случаях, коды получаемые из матриц Адамара Н _n(n ¹2^r), чаще всего являются нелинейными.

2.6.1. Доказать, что если n порядок матрицы Адамара, n ¹ 1 , 2, то n делится на 4.

2.6.2. Пусть u ₁,u ₂, . . . , u _n , n = 2^m, обозначают различные двоичные m- векторы. Доказать, что H _n= ( h _{i j} ) , где h _{i j} = ( - 1 )^Ui ^Uj является матрицей Адамара.

2.6.3. Построить коды Адамара А₈ , В₈ и С₈ .

2.6.4. Установить корректирующие возможности кодов А_n , В_n и С_n .

2.6.5. Определить скорости кодов А_n , В_n и С_n .

2.6.6. Построить матрицу Адамара порядка n = P^m+ 1, где Р - простое число.

2.6.7. Построить матрицы Адамара порядков 92, 116 и 172.

2.6.8. Построить коды Адамара для n = 92, 116 и 172.

2.6.9. Построить новые оптимальные коды на основе кодов Адамара

путём их склеивания.

2.6.10. Построить матрицу Адамара порядка 12n и соответствующие коды Адамара.

2.6.11. Определить, при каких n коды Адамара нелинейны.

2. 7. ГРАНИЦЫ МОЩНОСТИ КОДОВ

Задача определения точного числа кодовых слов с заданными параметрами весьма сложная. Поэтому для определения оптимальности того или иного кода на практике необходимо получить соответствующие оценки относительно мощности кодов.

Рассмотрим основные нижние и верхние границы относительно мощности двоичных кодов, т.е. когда алфавит канальных символов представляет собой поле Галуа GF( 2 ).

Итак, пусть С некоторый двоичный ( n , M , d ) - код, т.е. код длины n, мощности M и с минимальным расстоянием d. Обозначим через В ( n , d ) и M ( n , d ) максимальные мощности линейного и нелинейного (или линейного ) кодов соответственно длины n с минимальным расстоянием d. Эти величины фактически определяют скорость передачи информации с помощью данного кода и его корректирующие возможности.

Код С назовём оптимальным, если он имеет максимальную мощность среди всех кодов с той же корректирующей способностью и с теми же параметрами.

В общем случае имеет место неравенство

В ( n , d ) £ M ( n , d ) £ 2 ⁿ ,

т.е. оптимальные коды необходимо искать среди нелинейных кодов, где меньше всего порядка, в отличие от линейных кодов.

Так, например, код с проверкой на чётность С₀ длины n имеет мощность В ( n , 2 ) = 2 ^{n - 1} и является оптимальным.

В силу того, что

M ( n , 2 t ) = M ( n - 1 , 2 t - 1 ) ,

мы в дальнейшем рассмотрим лишь коды с минимальным нечётным расстоянием d = 2 t + 1.

I. Граница сферической упаковки ( граница Хэмминга ). Если существует двоичный код длины n, исправляющий t ошибок и содержащий

M ( n , 2 t + 1) кодовых слов, то должно выполняться неравенство

M ( n , 2 t + 1) £ 2 ⁿ / å C _nⁱ .

^{i = 0}

В самом деле, если х ₁, х₂ , . . . , х _{M ( n , 2 t + 1)} - все кодовые слова оптимального кода, для которых d ( x _i, x _j) ³ 2 t + 1 , i ¹j, то сферы радиуса t с центрами в кодовых словах не пересекаются ( сферой радиуса t с центром х_i называется множество всех слов х таких, что d ( x , х_i ) £ t ). Так как объём V_n^tодной сферы равен V_n^t = 1 + C _n¹+ . . . + C _n^t, то

M ( n , 2 t + 1) V_n^t £ 2 ⁿ,

откуда и следует граница Хэмминга:

M ( n , 2 t + 1) £ 2 ⁿ / å C _nⁱ .

^{i = 0}

Для кодов Хэмминга имеем t = 1, следовательно,

В ( n , 3 ) £ 2 ⁿ / ( n + 1 ).

Если же n = 2 ^r - 1, то имеет место равенство:

В ( n , 3 ) = 2 ⁿ / ( n + 1 ),

т.е. код Хэмминга длины n = 2 ^r - 1 также является оптимальным.

Код, мощность которого достигается границе Хэмминга, называется совершенным кодом или же плотно упакованным кодом.

В этом смысле код Хэмминга является совершенным кодом при n =2 ^r - 1. В общем случае для существования совершенного кода длины n, с кодовым расстоянием d = 2 t + 1 необходимо выполнение равенства

1 + C _n¹+ . . . + C _n^t = 2 ^r,

где r - некоторое натуральное число. Так, например, при n = 23 имеем:

1 + C¹₂₃+ С²₂₃+ C³₂₃ = 2¹¹ ,

т.е. t = 3, что соответствует совершенному коду G₂₃ Голея [ 23 , 12 , 7 ], исправляющего три или менее число ошибок.

II. Граница Гильберта. Имеет место неравенство

M ( n , 2 t + 1) ³ 2 ⁿ / å C _nⁱ .

^{i = 0}

Построим код с кодовым расстоянием d = 2 t + 1. Пусть х ₁ - произвольное первое кодовое слово из GFⁿ (2). Далее к коду добавим новое слово х ₂, лежащее вне шара радиуса 2 t с центром в х ₁. На следующем шаге в качестве очередного нового кодового слова выберем х ₃, не принадлежащее шарам радиуса 2 t, описанным вокруг х ₁ и х ₂ соответственно. Процедура завершается после того, когда уже выбраны х ₁ , х ₂ , . . . , х _Sслов и имеет место неравенство

S V_n²^t ³ 2 ⁿ ,

или

S ³ 2 ⁿ / V_n^{2 t} ,

где V_n^{2 t} - объём шара радиуса 2 t. Но мощность оптимального кода не меньше мощности таким образом построенного кода, следовательно,

M ( n , 2 t + 1) ³ 2 ⁿ / å C _nⁱ ,

^{i = 0}

что и соответствует нижней границе Гильберта.

Так, например, для кода Хэмминга длины n = 2 ^r - 1, имеем

В ( n , 3 ) ³ 2 ^{n + 1} / ( n ² + n + 2 ).

III. Граница Варшамова-Гильберта. Если выполняется неравенство

1 + C _{n - 1}¹+ . . . + C _{n - 1}^{d - 2} < 2 ^r,

то существует двоичный линейный код длины n с минимальным расстоянием по крайней мере d, имеющий не более чем r проверочных символов.

Идея получения этой границы сводится к построению проверочной матрицы H размерности ( r´n ) , любые d - 1 столбцов которой линейно независимы.

IV. Граница Плоткина. Для любого ( n , M , d ) - кода С при n < 2 d справедливо неравенство

М( n , d ) £ 2 [ d / (2d - n) ].

Доказательство этой границы предоставляется читателю.

V. Граница Джонсона. Если M( n , d , w ) мощность оптимального равновесного кода длины n, с минимальным расстоянием d и веса w, то имеет место неравенство

М( n , 2d , w ) £ [ dn / (w ² - wn + dn)]

при условии , что знаменатель положителен (код называется равновесным веса w, если все его слова имеют один и тот же вес w ).

2.7.1. Доказать, что М( n , d ) £ t /d +1, где t - общее число единиц кода.

2.7.2. Пусть s и t число нулевых и единичных разрядов соответственно для кодов С и С +1. Доказать, что

a ) (s - n) / (n - d) + 1 £ M(n , d) £ t / d + 1;

b ) (t - n) / (n - d) + 1 £ M(n , d) £ s / d + 1.

2.7.3. Доказать, что _{n - 1}

а ) M(n , d) £ n å C ^k_{n - 1}/ d + 1;

^{k = d - 1}

b ) M(n , d) £ n å C ^k_{n - 1}/ d + 1.

^{k = d}

2.7.4. Доказать, что код С₀ является оптимальным.

2.7.5. Упаковать все слова [ 7 , 4 , 3] - кода в пространстве GF⁷(2).

2.7.6. Определить число кодовых слов веса 3 кода H_r.

2.7.7. Определить число кодовых слов веса 4 расширенного кода H_r₊₁.

2.7.9. Доказать границу Варшамова - Гильберта для поля GF(q):

_d_{- 2}

å (q - 1) C ⁱ_n_{- 1} < q ^r .

ⁱ^{= 0}

2.7.10. При каких n и t число M ( n , 2 t + 1) есть степень двойки.

2.7.11.Оптимальны ли коды (10, 38, 4), (11, 72, 4), (12, 144, 4) ?

Дата добавления: 2019-02-13; просмотров: 666; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 Следующая ⇒

Мы поможем в написании ваших работ!