Показательное (экспоненциальное) распределение
Московский государственный университет путей сообщения
(миит)
Кафедра «Безопасность жизнедеятельности»
Б.Н. Рубцов
Расчетно-графические задачи
Для исследования полей и уровней
Поражающих факторов источников
Чрезвычайных ситуаций
Учебное пособие
Москва – 2009
Московский государственный университет путей сообщения
(миит)
Кафедра «Безопасность жизнедеятельности»
Б.Н. Рубцов
Расчетно-графические задачи для
Исследования полей и уровней
Поражающих факторов источников
Чрезвычайных ситуаций
Рекомендовано редакционно-издательским советом университета в качестве учебного пособия для студентов специальности «Безопасность жизнедеятельности в техносфере»
Москва – 2009
УДК 6583
Р82
Рубцов Б.Н. Расчетно-графические задачи для исследования полей и уровней поражающих факторов источников чрезвычайных ситуаций: Учебное пособие. – М.: МИИТ, 2009. – 140 c.
Учебное пособие разработано в рамках программы подготовки студентов университета по дисциплине «Общий курс безопасности в ЧС». Посвящено разработке и обобщению математического аппарата для расчетов полей и уровней поражающих факторов источников ЧС, а также вопросам устойчивости объектов в ЧС. Даны примеры расчетов по многим разделам программы. Будет полезно для преподавателей, аспирантов и студентов всех специальностей университета при ведении научно-исследовательских, лабораторных работ, практических занятий, выполнении курсовых работ и дипломных проектов по вопросам безопасности в ЧС.
|
|
|
Рецензенты
доцент РГТЭУ Рушанский В.Я.
зам.начальника
учебного отдела Мантуров Ф.С.
ИКБ МИИТа
© Московский государственный
университет путей сообщения
(МИИТ), 2009
Глава 1. Теоретические основы прогнозирования чрезвычайных ситуаций и их последствий
Общие положения
Прогноз – «основанное на специальном исследовании заключение о предстоящем развитии и исходе чего-нибудь» (прогноз погоды; прогноз события; и т.п.) [8].
Прогнозирование – научная деятельность по заблаговременному определению вероятности возникновения чрезвычайных ситуаций и их последствий на основе оценки риска. Или – «научная деятельность по установлению прогноза» [8].
Обстановка – условия, которые сложились или могут сложиться в районе (регионе, отдельном объекте) в результате произошедшей или возможной ЧС и их влияние на жизнедеятельность населения.
Любое решение на практические действия по ликвидации последствий ЧС должно основываться на выявлении и оценке обстановки.
|
|
|
Под выявлением обстановки понимается сбор и обработка исходных данных о ЧС, определение размеров зон чрезвычайных ситуаций и нанесение их на карту (план). Главная цель выявления обстановки – определить масштаб и степень поражений (разрушений), а также продолжительность действия поражающих факторов источников ЧС.
Под оценкой обстановки понимается решение основных задач по определению полей и уровней поражающих факторов источников ЧС и их воздействие на объекты и окружающую среду, жизнедеятельность населения, а так же выбора оптимальных мер защиты населения и дальнейших действий сил и средств по ликвидации последствий ЧС.
Потери населения в ЧС [4,5] – включают все людские потери, возникшие при ЧС. Они подразделяются на безвозвратные и санитарные.
К безвозвратным потерям относят погибших до оказания медицинской помощи; к санитарным – пораженных (оставшихся в живых), но утративших работоспособность (боеспособность) и поступивших в лечебные учреждения или медицинские пункты.
Пораженный в ЧС - человек, заболевший, травмированный или раненый в результате поражающего воздействия источника ЧС. [5].
|
|
|
Разрушение объекта экономики – результат поражающего воздействия, вследствие которого объекты полностью или частично (временно) теряют способность к нормальной работе (выпуску продукции). [5].
Поражения людей по их тяжести принято делить на смертельные, крайне тяжелые, средней тяжести и легкие.
Риск – возможная опасность какой-либо неудачи, возникшая в связи с предпринимаемыми действиями, а также сами действия, при которых достижение желаемого результата связано с такой опасностью [5] или «…возможность опасности, неудачи…» [8]. Понятие риска связывают с возможностью наступления сравнительно редких событий. При этом риск часто отождествляют с вероятностью наступления этих событий за интервал времени (как правило, за год.). Вероятность выступает в этом случае как мера (показатель) риска.
Риск связывают также с размером ущерба от опасного события в натуральном или стоимостном выражении. В формализованном виде наиболее общий показатель риска имеет вид:
Показатель риска (ущерб/время) = частота (события/время) × средний ущерб (ущерб/события).
Т.О. независимыми переменными, по которым оценивается риск, являются время и ущерб, а для оценки (прогноза) риска необходимо определять частоты реализаций опасных событий и ущерб от них.
|
|
|
Таблица 1.1. Частоты некоторых опасных событий
| Опасное событие | Частота/год |
| Техногенные ЧС, в том числе: пожары и взрывы аварии на трубопроводах крупные автомобильные катастрофы крупные крушения на ж/д | (0,9-1,2)Е10-3 350-450 60-80 120-150 15-20 |
| Природные ЧС, в том числе: лесные пожары (площадь >100га) бури, ураганы, смерчи, шквалы | 200-500 100-200 80-120 |
| Биолого-социальные ЧС | 100-150 |
Различают риски: индивидуальный риск – это мера возможности наступления негативных последствий для здоровья из-за действия на человека в течение определенного времени опасных факторов; коллективный риск – интегральная характеристика опасностей определенного вида в конкретном районе и характеризует масштаб возможной аварии (оценивается числом смертей на рассматриваемую совокупность людей).
Различают также: добровольный риск (относится к личной жизни – например, альпинизм, прыжки с парашютом и др.); вынужденный риск (связан с необходимостью выполнять профессиональные обязанности в определенных действиях).
Понятие риска в настоящее время широко используется в науке и практике.
Анализ риска для населения и территорий от ЧС основан на использовании различных концепций, методов и методик (рис 1.1).
| Анализ риска |
| Техническая |
| Экономи-ческая |
| Психологи-ческая |
| Социальная |
| Феноменоло-гический |
| Детерминис-тский |
| Вероятностный |
| Статистическая |
| Теоретико-вероятностная |
| Эвристическая |
| Концепции |
| Методы |
| Методики |
Рис.1.1. Методический аппарат анализа риска
Методы оценки риска: феноменологические; детерминистские и вероятностные.
Исследование риска для населения и территорий от ЧС на основе вероятностного метода, позволяет применить различные методики оценки риска. В зависимости от имеющейся исходной информации это могут быть методики следующих видов:
- статистическая, когда вероятности определяются по имеющимся статистическим данным (при их наличии);
- теоретико-вероятностная, используемая для оценки рисков от редких событий, когда статистика практически отсутствует;
-эвристическая, основанная на использовании субъективных вероятностей, когда отсутствуют не только статистические данные, но и математические модели.
На рис. 1.2. показана классификация методов прогноза рисков катастроф и стихийных бедствий, а в табл. 1.2. представлены подходы к прогнозированию ЧС.
Вероятностно-статический подход основан на представлении природных явлений на рассматриваемой территории или аварий на совокупности однотипных объектов пуассоновским потоком случайных событий. Используется для оценивания частот экстремальных природных явлений с силой не менее заданной и аварийных ситуаций определенного вида.
| По назначению |
| По времени проведения |
| Методы |
| По параметрам |
| По времени упреждения |
| Прогноз риска ЧС |
| Прогнозирование возникновения |
| Прогнозирование последствий |
| Место |
| Сила |
| Время |
| Частота |
| Априор-ные |
| Апосте-риорные |
| Долго-срочный |
| Кратко-срочны |
| Средне-срочный |
| Заблаго-временно |
| Оперативно по факту |
| Вероят-ностно-статисти-ческий |
| Вероят-ностно-детерми-нирован-ный |
| Детерми-ниро-ванно-вероят-ностный |
| Экспе-римен-тальные |
| Расчетно-экспери-менталь-ные |
| Расчет-ные (по мо-делям) |
| По исходным данным |
Рис. 1.2. Методический аппарат прогноза риска
Вероятностно-детерминированный подход основан на установлении законов и закономерностей развития природных процессов во времени и пространстве, цикличности природных явлений, что можно использовать для целей их долгосрочного и среднесрочного прогнозирования. Если имеется циклически действующий фактор, то свойство отсутствия последствия нарушается, и поток природных явлений не подчиняется закону Пуассона.
Таблица 1.2. Подходы к прогнозированию ЧС
| Подход | Интервал упреждения, исходная информация | Аппрок-симация модели | Прогнозиру-емый показатель | Меры по снижению рисков и смягчению последствий ЧС |
| Вероят-ностно-статисти-ческий | Оценка частоты по данным многолетних наблюдений | Пуассо-новский поток, F ИС ( u ) | a ИС ( Δt / u ИС ≥ un ) на рассматрива-емой территории | Меры по ограничению антропогенной деятельности (налоги на выбросы в атмосферу); предупреждение (снижение силы) некоторых природных явлений; регулирование застройки на основе районирования территории и т.д. |
| Вероятно-стно-детермини-рованный | Долгосрочный (годы) прогноз времени наступления по данным многолетних наблюдений | Цикли-чность, унимо-дальные распреде-ления F ИС ( t ) | t ИС ( u ИС ≥ un ), QИС ( Δt / t *) на рассматри-ваемой территории | |
| Среднесрочный прогноз места и времени (месяцы, недели) наступления по данным мониторинга | Модели возникно-вения и развития экстре-мальных природных явлений | t ИС ( x ИС , u ИС ≥ un ) | Повышение защищенности территорий; обучение населения и аварийно-спасательных формирований действиям в условиях ЧС | |
| Детерми-нированно-вероят-ностный | Краткосрочный прогноз места, силы и времени наступления (дни, часы) по предвестникам | t ИС , x ИС , u ИС | Смягчение последствий (оповещение; эвакуация, своевременное начало аварийно-спасательных работ) |
Детерминировано-вероятностный подход используется для краткосрочного прогнозирования (с учетом предвестников и оперативной информации о приближающемся событии, а также неопределенностей методик прогноза их развития и перемещения). При этом кроме времени наступления события прогнозируется его место и сила. Подход применим и для прогнозов аварий на технических объектах с непрерывным контролем технического состояния.
Прогнозирование последствий ЧС можно представить следующей блок-схемой (рис.1.3).
| Исходные данные - возможные поражающие факторы; - характеристика объекта; - размещение населения; - климатические и погодные условия; - рельеф местности; - наличие потенциально опасных объектов; - другие данные. |
| Формирование модели воздействия |
| Формирование моделей: - сопротивления воздействию; - разрушения зданий и сооружений; - поражения людей; - завалов и др. |
| Прогнозирование обстановки - инженерной; пожарной; химической и радиационной; медицинской и др. |
| Прогноз последствий первичного воздействия |
| Прогноз последствий вторичного воздействия |
Рис.1.3. Блок-схема прогнозирования исследований ЧС
мирного и военного времени
Законы поражения
Координатный закон поражения
Этим законом можно представить зависимость вероятности поражения (разрушения) объекта не ниже заданной степени тяжести (ущерба) от его положения (координат) относительно центра (эпицентра) поражающего фактора (например, взрыва). Для каждой интенсивности воздействия поражающего фактора (его параметра) существует определенная закономерность изменения вероятности определенной степени поражения (разрушения) данного объекта в зависимости от его расстояния от центра воздействия. Вследствие симметричного воздействия поражающих факторов взрыва относительно его центра на среднепересеченной местности координатный закон поражения будет круговым. Начало координат совмещается с центром, а на оси абсцисс указывается R – расстояние от центра взрыва, а на оси ординат – вероятность G поражения (разрушения) определенного элемента с заданной степенью тяжести. При рассмотрении этого закона можно выделить три зоны (области), расположенные вокруг центра взрыва (рис. 1.4).
В зоне радиусом Rд, непосредственно примыкающей к центру взрыва, вероятность поражения объекта постоянна и равна 1; эту зону принято называть зоной безусловного (достоверного) поражения.
Рис. 1.4. Графическое изображение кругового координатного закона поражения
a – поражение не ниже средней степени тяжести;
б – поражение не ниже легкой степени тяжести.
За ней следует зона с радиусом Ra, в пределах которой вероятность поражения уменьшается с 1 до 0; эту зону называют зоной вероятного поражения. Затем располагается зона с радиусом Rб>Rа, в пределах которой не будут наблюдаться поражения средней тяжести. Начиная с R>Rб будут отсутствовать и легкие повреждения; эту зону принято называть зоной полной безопасности.
В практических целях для удобства расчетов вид координатного закона поражения можно упростить, искусственно расширив зону достоверных поражений за счет зоны вероятных поражений. Такую зону называют приведенной зоной поражения, в пределах которой объект (цель) поражается с заданной вероятностью. При таком подходе координатный закон поражения заменяется простым одноступенчатым законом вероятности поражения объекта (цели) от расстояния до объекта R, G = f(R) (рис. 1.5). Размер приведенной зоны поражения можно характеризовать радиусом Rn, м (км).
Рис.1.5. Графическое изображение одноступенчатого
закона вероятности поражения объекта
Для всех точек приведенной зоны поражения вероятность поражения объекта (цели) со степенью не ниже заданной равна 1, а вне этой зоны (R>Rn) – равна нулю.
На границе приведенной зоны поражения R=Rn вероятность поражения объекта (цели) составляет 0,5. Приведенная зона поражения Sn (м2) имеет вид круга – Sn=πRn2.
Т.О. использование кругового одноступенчатого закона вероятности поражения объекта позволяет оперативно с приемлемой для ручных расчетов точностью оценивать степени поражения (разрушения) объектов на определенной площади.
Ущерб, наносимый объекту М, % может быть вычислен как отношение количества пораженных элементов mn (часть площади объекта, оказавшаяся в зоне поражения Sn) к общему их числу на объекте mo (площади всего объекта), по соотношению M= 
или М= 
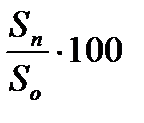(в процентах).
Для определения ущерба (потерь) необходимо знать значения радиусов зон поражения (выхода из строя) личного состава (зданий, сооружений и др. техники) и степень их защищенности на объекте, а так же взаимные расположения центра (эпицентра) взрыва и центра объекта. Кроме этого, необходимо знать характер распределения людей, техники, зданий и сооружений на объекте. Зачастую такая информация будет отсутствовать. Поэтому условно необходимо принимать, что все элементы на объекте распределены равномерно.
Возможные варианты взаимного расположения центров объекта и источника ЧС показаны на рис. 1.6.
Рис. 1.6. Расположение зон поражения
относительно площади объекта (вариант)
При оценке абсолютных потерь людей Пл и техники (зданий, сооружений) Nт, находящейся на объекте, следует определять площадь объекта Sn, накрытую зоной поражения, и умножить на количество людей Nл и техники Nт, находящихся на объекте, т.е. Пл=Nл·Sn/So и Пт=Nт·Sn/So.
Параметрический закон
Параметрический закон поражения определяет зависимость вероятности поражения объекта от интенсивности поражающего фактора источника ЧС (одного из его параметров).
Функции распределения F(x) поражающих факторов и плотность вероятности случайной величины определяют на основе статистической обработки или расчетным путем. В качестве случайных величин могут приниматься любые параметры поражающих факторов. Ими могут быть: интенсивность землетрясения в баллах; избыточное давление воздушной ударной волны или ее удельный импульс при взрывах; тепловой поток или тепловая доза и др. параметры поражающего фактора.
Рис. 1.7. Законы распределения поражающих факторов
а – функция распределения случайной величины
F(x)=G(x<x) (1.1)
б – функция распределения плотности вероятностей
f(x)=F’(x) (1.2)
x – поражающий фактор (случайная величина)
F(x)= 
(1.3)
Показательное (экспоненциальное) распределение
Аналогом закона Пуассона для непрерывных случайных величин служит показательный (экспоненциальный) закон, функция плотности распределения которого имеет вид:
| f(x)= | 0 при х<0, |
| λe-λx при х≥0, |
(1.4)
где λ>0 – постоянный параметр.
Функция распределения (интегральная функция) показательного закона:
F(x) = 
= 1 – e-λx, (1.5)
| т.е. F(x)= | 0 при х<0, |
| 1– e– λx при х≥0. |
(1.6)
Вероятность попадания случайной величины Х в интервал (α,β) составляет
G(α<X<β)=F(β) –F(α)=(1– e- λ β) – (1–e- λ α)=e- λ α–e- λ β, (1.7)
т.е. G(α<x<β)=e- λ α – e-λ β.
Числовые характеристики показательного закона распределения (даются без вывода):
– математическое ожидание М(х)= 
; (1.8)
– дисперсия D(x)= 
; (1.9)
– среднее квадратичное отклонение σ(х)= 
. (1.10)
На рис. 1.8. показаны типичные виды нормального и степенного распределений. В нормальном (гауссовом) распределении (жирная линия) вероятность отклонения случайной величины от среднего значения более чем на три «сигмы» (среднеквадратичного отклонения) составляет менее 0,001 и ими пренебрегают. В степенном законе (тонкая кривая) «хвост» убывает гораздо медленнее, и пренебрегать большими отклонениями нельзя. Многие бедствия, аварии, катастрофы порождают статистику со степенным распределением. В этом случае редкими катастрофическими событиями пренебречь нельзя. В логарифмическом масштабе степенные зависимости приобретают вид прямых линий.
Рис. 1.8 . Типичный вид нормального и степенного
распределений
Дата добавления: 2019-02-12; просмотров: 298; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!