Системы эконометрических уравнений
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ ТАТАРСТАН
ГАОУ ВПО «Альметьевский государственный институт
муниципальной службы»
Кафедра информатики и математики
Эконометрика
Программа, методические указания и контрольные задания для
Студентов заочников специальности080109 Бухгалтерский учет,анализ и аудит.
Альметьевск 2011
УДК 51-77
ББК 22.1
Е51
Рецензент: Кулагин В.А. кандидат физико-математических наук, профессор МОСИ
Микка К.В. кандидат физико-математических наук, доцент МарГТУ
Елисеева С.В.
Методические указания по решению контрольной работы
(самостоятельная работа студентов)
II курса специальности 080109. Бухгалтерский учет, анализ и аудит.
Е51 С.В.Елисеева – Альметьевск: ИИЦ АГИМС, 2011. – 40с.
© С.В.Елисеева, 2011
© ИИЦ АГИМС, 2011
Введение
Методические указания составлены для студентов-заочников специальности «Бухгалтерский учет, анализ и аудит», содержат программу курса эконометрики, указания к выполнению заданий контрольной работы, варианты заданий и необходимые для решения задач статистические таблицы.
Студенты выполняют четыре задания. Номер варианта контрольной работы выбирается студентом в соответствии с первой буквой своей фамилии.
| Номер варианта | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Первая буква фамилии студента | А | Г | Ж | И | Л | О | С | Ф | Ч | Э |
| Б | Д | З | К | М | П | Т | Х | Ш | Ю | |
| В | Е | Н | Р | У | Ц | Щ | Я |
При решении заданий студенты могут использовать таблицы статистических данных, приведенные в приложениях.
Используются количественные данные для наблюдения за ходом развития экономики, ее анализа и прогнозов. Набор статистических методов, используемых для этих целей, называется в совокупности эконометрикой. Современное экономическое образование базируется, в основном, на макроэкономике, микроэкономике и эконометрике. Для выработки управленческих решений, составления социально-экономических прогнозов, оптимизации принимаемых решений и выработки правильной социально-экономической политики успешно применяются эконометрические методы.
Программа курса эконометрики предполагает использование при изучении курса во всех его разделах вычислительной техники и пакетов прикладных программ.
Цель преподавания эконометрики – ознакомить студентов с основами математического и эконометрического моделирования необходимых для решения теоретических и практических экономических задач; развивать логическое мышление; привить навыки самостоятельного изучения учебной и научной литературы; повысить общий уровень использования количественных методов в экономических исследованиях; выработать навыки исследования с помощью математических моделей и персональных компьютеров.
Программа курса эконометрики
Введение. Предмет и содержание курса эконометрики. Методология эконометрических исследований. Математическая и эконометрическая модель.
Раздел 1. Регрессионная модель. Классическая линейная регрессия в случае одной объясняющей переменной. Множественная линейная регрессия в скалярной и векторной формах. Метод наименьших квадратов (МНК); свойства МНК-оценок; показатели качества регрессии. Теорема Гаусса-Маркова для множественной линейной регрессионной модели. Линейные регрессионные модели с гетероскедастичными и автокоррелированными остатками. Обобщенный метод наименьших квадратов (ОМНК). Регрессионные модели с переменной структурой (фиктивные переменные). Нелинейные модели и их линеаризация. Коэффициент множественной детерминации. Различные аспекты множественной регрессии.
Раздел 2. Системы одновременных регрессионных уравнений (СОУ). Основные понятия СОУ: экзогенные и эндогенные переменные; структурная и приведенная формы системы одновременных уравнений. Условия идентифицируемости СОУ, идентификация рекурсивных систем. Косвенный, двухшаговый и трехшаговый методы наименьших квадратов. Применение СОУ.
Раздел 3. Анализ временных рядов. Понятие временного ряда и его компоненты. Аддитивные и мультипликативные модели временных рядов. Модели стационарных и нестационарных временных рядов, их идентификация. Модели распределенных лагов. Модели Бокса-Дженкинса (ARIMA)
Задание № 1
Парная регрессия
Парная регрессия – уравнение связи двух переменных  и
и  :
:
 ,
,
где 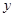 – зависимая переменная (результативный признак);
– зависимая переменная (результативный признак);
 – независимая переменная (признак – фактор).
– независимая переменная (признак – фактор).
Построение уравнения регрессии  или
или  сводится к оценке ее параметров. Для оценки параметров регрессий, линейных по параметрам, используют метод наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака
сводится к оценке ее параметров. Для оценки параметров регрессий, линейных по параметрам, используют метод наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака 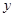 от теоретических
от теоретических  минимальна, т.е.
минимальна, т.е.
 .
.
Чтобы найти минимум функции, надо вычислить частные производные по каждому из параметров  ,
,  и приравнять их к нулю:
и приравнять их к нулю:

Преобразуя последнюю систему, получим

Решая систему уравнений, получим
 .
.
Тесноту связи изучаемых явлений оценивает коэффициент парной корреляции 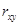 для линейной регрессии
для линейной регрессии  :
:  ,
,
и индекс корреляции 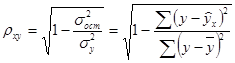 .
.
Близость 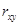 к нулю означает отсутствие линейной связи между признаком и фактором.
к нулю означает отсутствие линейной связи между признаком и фактором.
Средний коэффициент эластичности  позволяет проверить, имеют ли экономический смысл коэффициенты модели регрессии.
позволяет проверить, имеют ли экономический смысл коэффициенты модели регрессии.
Из дисперсионного анализа известно, что
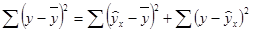 ,
,
где  – общая сумма квадратов отклонений;
– общая сумма квадратов отклонений; 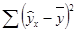 – сумма квадратов отклонений, обусловленная регрессией;
– сумма квадратов отклонений, обусловленная регрессией;  – остаточная сумма квадратов отклонений.
– остаточная сумма квадратов отклонений.
Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака 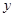 характеризует коэффициент (индекс) детерминации
характеризует коэффициент (индекс) детерминации
 .
.
Коэффициент детерминации – квадрат коэффициента или индекса корреляции.
F-тест – оценивание качества уравнения регрессии – состоит в проверке гипотезы  о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического
о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического  , и критического (табличного)
, и критического (табличного)  значений F-критерия Фишера.
значений F-критерия Фишера.
 определяется по формуле
определяется по формуле
 ,
,
где  – число единиц совокупности;
– число единиц совокупности;  – число параметров при совокупности
– число параметров при совокупности  .
. 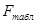 – это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости
– это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости  . Уровень значимости
. Уровень значимости  – вероятность отвергнуть правильную гипотезу. Обычно
– вероятность отвергнуть правильную гипотезу. Обычно  принимается равной 0,05 или 0,01.
принимается равной 0,05 или 0,01.
Если  <
<  , то
, то  - гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность. Если
- гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность. Если 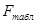 >
>  , то гипотеза
, то гипотеза  не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии.
не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии.
Для оценки существенности отдельных параметров уравнения определяется их стандартная ошибка  и
и  :
:
 ,
,
где  – остаточная дисперсия на одну степень свободы.
– остаточная дисперсия на одну степень свободы.
Величина  имеет
имеет  -распределение Стьюдента с
-распределение Стьюдента с  степенями свободы, которое затем сравнивается с табличным значением при определенном уровне значимости
степенями свободы, которое затем сравнивается с табличным значением при определенном уровне значимости  , заметим, что
, заметим, что  .
.
Доверительный интервал для коэффициента регрессии определяется как 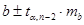 .
.
Стандартная ошибка параметра  определяется по формуле
определяется по формуле
 .
.
Процедура оценивания значимости данного параметра ничем не отличается от процедуры оценки значимости коэффициента регрессии  .
.
Точечный прогноз  значения признака часто бывает нереальным и дополняется расчетом стандартной ошибки
значения признака часто бывает нереальным и дополняется расчетом стандартной ошибки  и соответственно интервальной оценкой прогнозного значения
и соответственно интервальной оценкой прогнозного значения  :
:  ,
,
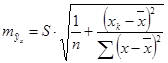 .
.
Для оценки качества модели определяется средняя ошибка аппроксимации:  , допустимые значения которой 8 - 10 %.
, допустимые значения которой 8 - 10 %.
ПРИМЕР 1. В табл. 1.1 приведены данные о годовой выручке (  ) от реализации продукции за десятилетний период.
) от реализации продукции за десятилетний период.
Таблица 1.1
| Год | 1990 | 1991 | 1992 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 |
| Выручка от реализации (млн у.е.) | 14 | 16 | 18 | 20 | 25 | 28 | 45 | 50 | 58 | 66 |
Требуется:
1. Для определения вида зависимости рассчитать параметры  и
и  функций: 1)
функций: 1)  , 2)
, 2) 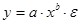 .
.
2. Определить тесноту связи и значимости параметров уравнения, используя F-распределение (Фишера) и  -критерий (Стьюдента), выбрав уровень значимости
-критерий (Стьюдента), выбрав уровень значимости  .
.
3. Рассчитать среднюю ошибку аппроксимации.
4. Рассчитать прогноз выручки от продаж при прогнозном значении фактора  , составляющим 102% от среднего уровня. Оценить точность прогноза и его доверительный интервал.
, составляющим 102% от среднего уровня. Оценить точность прогноза и его доверительный интервал.
5. Сделать выводы по результатам расчетов.
Решение. Присвоим каждому году соответствующий номер 1, 2, …, 10.
Составим таблицу расчетов 1.2.
Все расчеты в таблице велись по формулам
 .
.
Тогда  ,
,  и линейное уравнение регрессии примет вид:
и линейное уравнение регрессии примет вид: 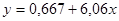 .
.
1. Рассчитаем коэффициент корреляции:
 .
.
Так как значение коэффициента корреляции близко к единице, то связь между признаком  и фактором
и фактором 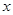 тесная.
тесная.
2. Вычислим значение 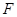 -критерия Фишера.
-критерия Фишера.
| |
|
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 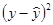
| А(%) | |
| 1 | 1 | 14 | 14 | 196 | -20 | -4,5 | 400 | 20,25 | 6,7273 | 7,2727 | 52,89 | 51,948 | ||
| 2 | 4 | 16 | 32 | 256 | -18 | -3,5 | 324 | 12,25 | 12,7879 | 3,2121 | 10,318 | 20,076 | ||
| 3 | 9 | 18 | 54 | 324 | -16 | -2,5 | 256 | 6,25 | 18,8485 | -0,848 | 0,7199 |
| ||
| 4 | 16 | 20 | 80 | 400 | -14 | -1,5 | 196 | 2,25 | 24,9091 | -4,909 | 24,099 | 24,5454 | ||
| 5 | 25 | 25 | 125 | 625 | -9 | -0,5 | 81 | 0,25 | 30,9697 | -5,97 | 35,637 | 23,8788 | ||
| 6 | 36 | 28 | 168 | 784 | -6 | 0,5 | 36 | 2,25 | 37,0303 | -9,03 | 81,548 | 32,2511 | ||
| 7 | 49 | 45 | 315 | 2025 | 11 | 1,5 | 121 | 6,25 | 43,0909 | 1,9091 | 3,6446 | 4,2424 | ||
| 8 | 64 | 50 | 400 | 2500 | 16 | 2,5 | 256 | 12,25 | 49,1515 | 0,8485 | 0,7199 | 1,69697 | ||
| 9 | 81 | 58 | 522 | 3364 | 24 | 3,5 | 576 | 20,25 | 55,2121 | 2,7879 | 7,7723 |  4,8067 4,8067
| ||
| 10 | 100 | 66 | 660 | 4356 | 32 | 4,5 | 1024 | 20,25 | 61,2727 | 4,7273 | 22,3471 | 7,1625 | ||

| 55 | 385 | 340 | 2370 | 14830 | 0 | 0 | 3270 | 82,5 | 239,697 | 175,32 | |||
| Среднее значение | 5,5 | 38,5 | 34 | 1483 | 1483 | 23,9697 | 17,532 | |||||||

| 2,87 | 18,08 | ||||||||||||

| 8,25 | 327 | ||||||||||||
|
 ,
,
где  – число параметров уравнения регрессии (число коэффициентов при объясняющей переменной
– число параметров уравнения регрессии (число коэффициентов при объясняющей переменной  );
);  – объем совокупности.
– объем совокупности.
 .
.
По таблице распределения Фишера находим  .
.
Так как  , то гипотеза
, то гипотеза  о статистической незначимости параметра
о статистической незначимости параметра  уравнения регрессии отклоняется.
уравнения регрессии отклоняется.
Так как  , то можно сказать, что 92,7% результата объясняется вариацией объясняющей переменной.
, то можно сказать, что 92,7% результата объясняется вариацией объясняющей переменной.
Средняя ошибка аппроксимации  вышла за допустимые пределы (8 - 10%), что говорит о ненадежности выбранной модели регрессии.
вышла за допустимые пределы (8 - 10%), что говорит о ненадежности выбранной модели регрессии.
Выберем в качестве модели уравнения регрессии 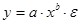 , предварительно линеаризовав модель. Прологарифмируем обе части равенства:
, предварительно линеаризовав модель. Прологарифмируем обе части равенства:  .
.
Введем обозначения:  ,
,  . Получим линейную модель регрессии
. Получим линейную модель регрессии 
Рассчитаем коэффициенты модели, поместив все промежуточные расчеты в табл. 1.3.
Таблица 1.3
|
| 
| 
| 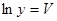
| 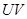
| 
| 
| 
|
| 0 | 0 | 2,639057 | 0 | 6,964624 | -0,74094 | -1.51 | |
| 0,693147 | 0,480453 | 2,772589 | 1,921812 | 7,687248 | -0,60741 | -0,81685 | |
| 1,098612 | 1,206949 | 2,890372 | 3,175398 | 8,354249 | -0,48963 | -0,41139 | |
| 1,386294 | 1,921812 | 2,995732 | 4,152967 | 8,974412 | -0,38427 | -0,12371 | |
| 1,609438 | 2,59029 | 3,218876 | 5,180581 | 10,36116 | -0,16112 | 0,099438 | |
| 1,791759 | 3,210402 | 3,332205 | 5,970509 | 11,10359 | -0,0478 | 0,281759 | |
| 1,94591 | 3,786566 | 3,806662 | 7,407423 | 14,49068 | 0,426662 | 0,43591 | |
| 2,079442 | 4,324077 | 3,912023 | 8,134823 | 15,30392 | 0,532023 | 0,569442 | |
| 2,197225 | 4,827796 | 4,060443 | 8,921705 | 16,4872 | 0,680443 | 0,687225 | |
| 2,302585 | 5,301898 | 4,189655 | 9,647037 | 17,55321 | 0,809655 | 0,792585 | |

| 15,10441 | 27,65024 | 33,81761 | 54,51225 | 117,2803 | ||
| Среднее значение | 1,510441 | 2,765024 | 3,381761 | 5,451225 | 11,72803 | ||

| 0,6954 | 0,507379 | |||||

| 0,483592 | 0,2574336 |
Окончание таблицы 1.3
|
| 
| 
| 
| 
| 
| А(%) |
| 0,548996 | 2,2801 | 13,96005 | 0,039946 | 0,001596 | 0,2853 | |
| 0,368948 | 0,667249 | 19,65511 | -3,65511 | 13,35984 | 22,8444 | |
| 0,239736 | 0,16924 | 24,01011 | -6,01011 | 36,12143 | 33,3895 | |
| 0,147662 | 0,015303 | 27,67349 | -7,67349 | 58,88244 | 38,3674 | |
| 0,025961 | 0,009888 | 30,89575 | -5,89575 | 34,75984 | 23,583 | |
| 0,002284 | 0,079388 | 33,80513 | -5,80513 | 33,6995 | 20,7326 | |
| 0,182041 | 0,190018 | 36,4777 | 8,522295 | 72,62951 | 18,9384 | |
| 0,283048 | 0,324264 | 38,96299 | 11,03701 | 121,8155 | 22,074 | |
| 0,463003 | 0,472278 | 41,29536 | 16,70464 | 279,0451 | 28,8011 | |
| 0,655541 | 0,628191 | 43,49979 | 22,50021 | 506,2597 | 34,0912 | |

| 243,1071 | |||||
| Среднее значение | 24,3107 |
1. Рассчитаем параметры уравнения, предварительно рассчитав
 ,
, 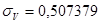 .
.
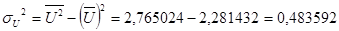 ,
,  .
.
 ,
,
 ,
,


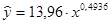 .
.
2. Коэффициент корреляции
 .
.
Коэффициент детерминации
 ,
,
следовательно, только 46,24% результата объясняется вариацией объясняющей переменной  .
.
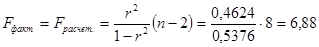 ,
,

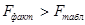 ,
,
следовательно, гипотеза  о статистической незначимости уравнения регрессии отклоняется. По всем расчетам линейная модель надежнее, и последующие расчеты мы сделаем для нее.
о статистической незначимости уравнения регрессии отклоняется. По всем расчетам линейная модель надежнее, и последующие расчеты мы сделаем для нее.
|
 .
.
Используем для этого t-распределение (Стьюдента). Выдвигаем гипотезу  о статистической незначимости параметров, т.е.
о статистической незначимости параметров, т.е.  .
.
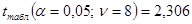 .
.
Определим ошибки  .
.
 ,
,
 ,
,
 ,
,  ,
,
 ,
,  .
.
Следовательно,  и
и  не случайно отличаются от нуля, а сформировались под влиянием систематически действующей производной.
не случайно отличаются от нуля, а сформировались под влиянием систематически действующей производной.
3.  , следовательно, качество модели не очень хорошее.
, следовательно, качество модели не очень хорошее.
4. Полученные оценки модели и ее параметров позволяют использовать ее для прогноза.
Рассчитаем  . Тогда
. Тогда  .
.
5. Средняя ошибка прогноза
 ,
,
где
 ,
,
 .
.
Строим доверительный интервал с заданной доверительной вероятностью  :
:
 ,
,
 ,
,
 .
.
Найденный интервальный прогноз достаточно надежен (доверительная вероятность  ) и достаточно точен, т.к.
) и достаточно точен, т.к.  .
.
КОНТРОЛЬНОЕ ЗАДАНИЕ 1
Задачи 1-5
Имеются данные за 12 месяцев года по району города о рынке вторичного жилья (y – стоимость квартиры (тыс. у.е.), x – размер общей площади (м2)). Данные приведены в табл. 1.4.
Таблица 1.4
| Мес. | Задача 1 | Задача 2 | Задача 3 | Задача 4 | Задача 5 | |||||
| y | x | y | x | y | x | y | x | y | x | |
| 1 | 13,0 | 37,0 | 13,2 | 37,2 | 22,5 | 46,0 | 22,5 | 29,0 | 23,0 | 22,8 |
| 2 | 16,4 | 60,0 | 15,9 | 58,2 | 25,5 | 54,0 | 25,8 | 36,2 | 26,8 | 27,5 |
| 3 | 17,0 | 60,9 | 16,2 | 60,8 | 19,2 | 50,2 | 20,8 | 28,9 | 28,0 | 34,5 |
| 4 | 15,2 | 52,1 | 15,4 | 52,0 | 13,5 | 43,8 | 15,2 | 32,4 | 18,4 | 26,4 |
| 5 | 14,2 | 40,1 | 14,2 | 44,6 | 25,4 | 78,6 | 25,8 | 49,7 | 30,4 | 19,8 |
| 6 | 10,5 | 30,4 | 11,0 | 31,2 | 17,8 | 60,2 | 19,4 | 38,1 | 20,8 | 17,9 |
| 7 | 20,0 | 43,0 | 21,1 | 26,4 | 18,0 | 50,2 | 18,2 | 30,0 | 22,4 | 25,2 |
| 8 | 12,0 | 32,1 | 13,2 | 20,7 | 21,0 | 54,7 | 21,0 | 32,6 | 21,8 | 20,1 |
| 9 | 15,6 | 35,1 | 15,4 | 22,4 | 16,5 | 42,8 | 16,4 | 27,5 | 18,5 | 20,7 |
| 10 | 12,5 | 32,0 | 12,8 | 35,4 | 23,0 | 60,4 | 23,5 | 39,0 | 23,5 | 21,4 |
| 11 | 13,2 | 33,0 | 14,5 | 28,4 | 14,6 | 47,2 | 18,8 | 27,5 | 16,7 | 19,8 |
| 12 | 14,6 | 32,5 | 15,1 | 20,7 | 14,2 | 40,6 | 17,5 | 31,2 | 20,4 | 24,5 |
Задачи 6 – 10
Имеются данные о потребительских расходах на душу населения (y, руб.), средней заработной плате и социальных выплатах (x, руб.) по 16 районам региона. Данные приведены в табл. 1.5.
Таблица 1.5
|
Районы | Январь | Февраль | Март | Апрель | Май | |||||
| Задача 6 | Задача 7 | Задача 8 | Задача 9 | Задача 10 | ||||||
| y | x | y | x | y | x | y | x | y | x | |
| A | 416 | 1288 | 420 | 1305 | 440 | 1310 | 445 | 1310 | 450 | 1380 |
| B | 501 | 1435 | 512 | 1440 | 525 | 1490 | 537 | 1490 | 540 | 1530 |
| C | 403 | 1210 | 430 | 1230 | 450 | 1250 | 463 | 1255 | 470 | 1310 |
| D | 208 | 1190 | 230 | 1275 | 240 | 1280 | 251 | 1287 | 275 | 1355 |
| E | 462 | 1640 | 505 | 1700 | 545 | 1710 | 553 | 1720 | 564 | 1810 |
| F | 386 | 1420 | 402 | 1480 | 447 | 1497 | 453 | 1500 | 462 | 1520 |
| G | 399 | 1250 | 430 | 1305 | 469 | 1312 | 478 | 1320 | 495 | 1410 |
| H | 342 | 870 | 400 | 895 | 435 | 903 | 448 | 918 | 450 | 1000 |
Продолжение таблицы 1.5
| I | 354 | 740 | 410 | 775 | 442 | 787 | 453 | 794 | 460 | 810 |
| J | 558 | 910 | 585 | 1000 | 605 | 1012 | 627 | 1012 | 633 | 1051 |
| K | 302 | 1020 | 370 | 1035 | 352 | 1049 | 364 | 1058 | 377 | 1078 |
| L | 360 | 1050 | 384 | 1150 | 405 | 1207 | 419 | 1213 | 422 | 1231 |
| M | 310 | 1205 | 345 | 1215 | 376 | 1221 | 392 | 1225 | 405 | 1230 |
| N | 415 | 990 | 445 | 1010 | 462 | 1035 | 478 | 1042 | 483 | 1050 |
| O | 452 | 1042 | 485 | 1059 | 505 | 1064 | 521 | 1071 | 537 | 1095 |
| P | 450 | 1037 | 491 | 1051 | 500 | 1072 | 517 | 1093 | 529 | 1101 |
Задание:
1. Рассчитайте параметры уравнений регрессий  и
и 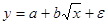 .
.
2. Оцените тесноту связи с показателем корреляции и детерминации.
3. Рассчитайте средний коэффициент эластичности и дайте сравнительную оценку силы связи фактора с результатом.
4. Рассчитайте среднюю ошибку аппроксимации и оцените качество модели.
5. С помощью F-статистики Фишера (при  ) оцените надежность уравнения регрессии.
) оцените надежность уравнения регрессии.
6. Рассчитайте прогнозное значение  , если прогнозное значение фактора увеличится на 5% от его среднего значения. Определите доверительный интервал прогноза для
, если прогнозное значение фактора увеличится на 5% от его среднего значения. Определите доверительный интервал прогноза для  .
.
7. Расчеты должны быть подробны, как показано в примере 1, и сопровождены пояснениями.
Задание 2
Множественная регрессия
Обобщением модели парной регрессии является модель множественной регрессии. Множественная регрессия – уравнение связи с несколькими независимыми переменными:
 ,
,
где  – зависимая переменная (результативный признак);
– зависимая переменная (результативный признак);
 – независимые переменные (факторы).
– независимые переменные (факторы).
Чаще всего используются линейные уравнения множественной регрессии:
 . (2.1)
. (2.1)
Используют также и нелинейные модели множественной регрессии, например:
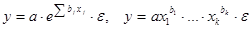 и др.
и др.
Построение модели связано с выбором вида уравнения и отбором факторов модели. Факторы, включаемые в модель, должны удовлетворять требованиям:
- должны быть количественно измеримы;
- не должны находиться в функциональной связи;
- между факторами не должно быть высокой корреляционной связи (не должны быть мультиколлинеарны).
Для выявления мультиколлинеарных факторов можно использовать корреляционную матрицу  :
:


где  – оценки коэффициентов парной корреляции. При этом, если факторы некоррелированы, то
– оценки коэффициентов парной корреляции. При этом, если факторы некоррелированы, то  , если между факторами линейная связь, то
, если между факторами линейная связь, то 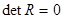 и чем ближе
и чем ближе 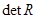 к нулю, тем сильнее мультиколлинеарность. Один из путей устранения мультиколлинеарности – исключение из модели одного или нескольких факторов.
к нулю, тем сильнее мультиколлинеарность. Один из путей устранения мультиколлинеарности – исключение из модели одного или нескольких факторов.
Для оценки параметров уравнения множественной регрессии используют МНК, для чего необходимо решить систему линейных уравнений

Другой вид уравнения множественной регрессии – уравнение регрессии в стандартизованном масштабе:
 ,
,
где  – стандартизованные переменные;
– стандартизованные переменные;
 – стандартизированные коэффициенты регрессии.
– стандартизированные коэффициенты регрессии.
Связь коэффициентов множественной регрессии  со стандартизованными коэффициентами
со стандартизованными коэффициентами  описывается соотношениями:
описывается соотношениями:
 .
.
Средние коэффициенты эластичности для линейной регрессии рассчитываются по формуле
 .
.
Для расчета частных коэффициентов эластичности применяется формула
 .
.
На основе уравнения (2.1) могут быть найдены частные уравнения регрессии:


Тесноту совместного влияния факторов на результат оценивает индекс множественной корреляции:
 .
.
Значение индекса множественной корреляции лежит в пределах от 0 до 1 и должно быть больше или равно максимальному парному индексу корреляции:
 .
.
Индекс множественной корреляции для уравнения в стандартизованном масштабе можно записать в виде:
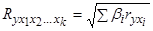 .
.
Частные коэффициенты (или индексы) корреляции, измеряющие влияние на  фактора
фактора  при неизменном уровне других факторов, можно определить по формуле
при неизменном уровне других факторов, можно определить по формуле
 .
.
Частные коэффициенты корреляции изменяются в пределах от –1 до 1.
Качество построенной модели в целом оценивает коэффициент (индекс) детерминации. Коэффициент множественной детерминации рассчитывается как квадрат индекса множественной корреляции:  .
.
Скорректированный индекс множественной детерминации содержит поправку на число степеней свободы и рассчитывается по формуле
 ,
,
где  – число наблюдений,
– число наблюдений,  – число факторов.
– число факторов.
Значимость уравнения множественной регрессии в целом оценивается с помощью F -критерия Фишера:
 .
.
Частный  -критерий оценивает статистическую значимость присутствия каждого из факторов в уравнении. В общем виде для фактора
-критерий оценивает статистическую значимость присутствия каждого из факторов в уравнении. В общем виде для фактора 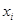 частный
частный  -критерий определится как
-критерий определится как
 .
.
Оценка значимости коэффициентов уравнения регрессии с помощью t-критерия Стьюдента сводится к вычислению значения
 ,
,
где 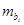 – средняя квадратическая ошибка коэффициента регрессии
– средняя квадратическая ошибка коэффициента регрессии 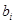 и определяется по формуле
и определяется по формуле
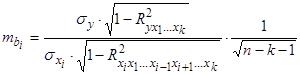 .
.
Возможны случаи, когда в модель регрессии необходимо включить факторы, имеющие атрибутивные признаки, например, образование, тип изделия, профессия и т.д.
Чтобы использовать эти переменные им придают численные значения. Такие искусственно сконструированные переменные в эконометрике называются фиктивными или структурными переменными.
Фиктивные переменные могут вводиться как в линейные, так и в нелинейные модели.
Пример 2. Изучается влияние стоимости основных оборотных средств на величину валового доходаторговых предприятий.
Для этого по двенадцати торговым предприятиям получены данные, приведенные в табл. 2.1.
Таблица 2.1
| Валовой доход (y), млн руб. | 203 | 63 | 45 | 13 | 121 | 88 | 110 | 56 | 80 | 237 | 160 | 75 |
| Среднегодовая стоимость основных фондов (x1) | 118 | 28 | 17 | 50 | 56 | 102 | 116 | 124 | 114 | 154 | 115 | 98 |
| Среднегодовая стоимость оборотных средств (x2) | 105 | 56 | 54 | 63 | 28 | 50 | 54 | 42 | 36 | 106 | 88 | 46 |
Требуется:
1. Построить уравнение множественной линейной регрессии в стандартизованной и естественной форме. Рассчитать частные коэффициенты эластичности.
2. Рассчитать линейные коэффициенты частной корреляции и коэффициент множественной корреляции.
3. Рассчитать общий и частные F-статистики Фишера.
4. По результатам расчетов сделать соответствующие выводы.
Решение. Результаты расчетов приведены в табл. 2.2.
Таблица 2.2
| y | x1 | x2 | yx1 | yx2 | x1x2 | x12 | x22 | y2 | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 203 | 118 | 105 | 23954 | 21315 | 12390 | 13924 | 11025 | 41209 | |
| 63 | 28 | 56 | 1764 | 3528 | 1568 | 784 | 3136 | 3969 | |
| 45 | 17 | 54 | 765 | 2460 | 918 | 289 | 2916 | 2025 | |
| 113 | 50 | 63 | 5650 | 7119 | 3150 | 2500 | 3969 | 12769 | |
| 121 | 56 | 28 | 6776 | 3388 | 1568 | 3136 | 784 | 14641 | |
| 88 | 102 | 50 | 8976 | 4400 | 5100 | 10404 | 2500 | 7744 | |
| 110 | 116 | 54 | 12760 | 5940 | 6264 | 13456 | 2916 | 12100 | |
| 56 | 124 | 42 | 6944 | 2352 | 5208 | 15376 | 1764 | 3136 | |
| 80 | 114 | 36 | 9120 | 2880 | 4104 | 12996 | 1296 | 6400 | |
| 237 | 154 | 106 | 36498 | 25122 | 16324 | 23716 | 11236 | 56169 | |
| 160 | 115 | 88 | 18400 | 14080 | 10120 | 13225 | 7744 | 25600 | |
| 75 | 98 | 46 | 7350 | 3450 | 4508 | 9604 | 2116 | 5625 | |

| 1351 | 1092 | 728 | 138957 | 96004 | 71222 | 119410 | 51402 | 191387 |
| Средн. | 112,58 | 91 | 60,67 | 11579,75 | 80000,3 | 5935,2 | 15948,92 | ||

| 57,219 | 39,457 | 24,549 | ||||||

| 3273,985 | 1556,8 | 602,68 |
Рассматриваем уравнение вида:
 .
.
Параметры уравнения можно найти из решения системы уравнений:

Или, перейдя к уравнению в стандартизированном масштабе:
 , где
, где  – стандартизированные переменные,
– стандартизированные переменные,  – стандартизированные коэффициенты:
– стандартизированные коэффициенты:

Коэффициенты  определяются из системы уравнений:
определяются из системы уравнений:


 ,
,  ;
;

 ;
;
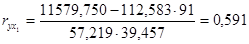 ,
,  ;
;
 ,
,  ;
;
 ,
,  ;
;
 ,
,  ;
;
 ,
,  ;
;
 .
.
Стандартизированная форма уравнения регрессии имеет вид:
 .
.
Естественная форма уравнения регрессии имеет вид:
 .
.
Для выяснения относительной силы влияния факторов на результативный признак рассчитываются средние коэффициенты эластичности:
 ,
,
 ,
,  .
.
Следовательно, при увеличении среднегодовой стоимости основных фондов (x1) на 1% валовой доход (y) увеличивается на 0,388% от своего среднего уровня. При повышении среднегодовой стоимости оборотных средств на 1% валовой доход повышается на 0,762% от своего среднего уровня.
2. Линейные коэффициенты частной корреляции для уравнения (2.1) определяются следующим образом:
 ,
,
 .
.
Отличие коэффициентов частной корреляции не слабой межфакторной связью (  ).
).
Линейный коэффициент множественной корреляции рассчитывается по формуле
 .
.
Коэффициент множественной детерминации 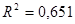 .
.
3.  , где
, где  - объем выборки,
- объем выборки,  - число факторов модели. В нашем случае
- число факторов модели. В нашем случае
 .
.
Так как  , то
, то  и потому уравнение значимо в целом.
и потому уравнение значимо в целом.
Выясним статистическую значимость каждого фактора в уравнении множественной регрессии.
Для этого рассчитаем частные  -статистики.
-статистики.
 .
.
Так как  , то
, то  и следует вывод о нецелесообразности включения в модель фактора
и следует вывод о нецелесообразности включения в модель фактора  после фактора
после фактора  .
.
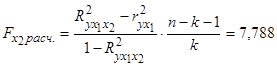 .
.
Так как  , то следует вывод о целесообразности включения в модель фактора
, то следует вывод о целесообразности включения в модель фактора  после фактора
после фактора  .
.
4. Результаты расчетов позволяют сделать вывод :
1) о незначимости фактора  и нецелесообразности включения его в уравнение регрессии;
и нецелесообразности включения его в уравнение регрессии;
2) о значимости фактора  и целесообразности включения его в уравнение регрессии.
и целесообразности включения его в уравнение регрессии.
В результате значимой оказалась модель  .
.
КОНТРОЛЬНОЕ ЗАДАНИЕ № 2
Задачи 11-15
Имеются данные о деятельности крупнейших компаний в течение двенадцати месяцев 199Х года. Данные приведены в табл. 2.3.
Известны – чистый доход (у), оборот капитала (х1), использованный капитал (х2) в млрд у.е.
Таблица 2.3
| Задача 11 | Задача 12 | Задача 13 | Задача 14 | Задача 15 | ||||||||||
| у | х1 | х2 | у | х1 | х2 | у | х1 | х2 | у | х1 | х2 | у | х1 | х2 |
| 5,5 | 53,1 | 27,1 | 6,6 | 6,9 | 83,6 | 3,6 | 16,2 | 13,3 | 1,5 | 5,9 | 5,9 | 3,0 | 18,0 | 6,6 |
| 2,4 | 18,8 | 11,2 | 3,0 | 18,0 | 6,5 | 1,5 | 5,9 | 5,9 | 5,5 | 53,1 | 27,1 | 3,3 | 16,7 | 15,4 |
| 3,0 | 35,3 | 16,4 | 6,5 | 107,9 | 50,4 | 5,5 | 53,1 | 27,1 | 2,4 | 18,8 | 11,2 | 3,6 | 16,2 | 13,3 |
| 4,2 | 71,9 | 32,5 | 3,3 | 16,7 | 15,4 | 2,4 | 18,8 | 11,2 | 3,0 | 35,3 | 16,4 | 5,5 | 53,1 | 27,1 |
| 2,7 | 93,6 | 25,4 | 0,1 | 76,6 | 29,6 | 3,0 | 35,3 | 16,4 | 4,2 | 71,9 | 32,5 | 3,0 | 35,3 | 16,4 |
| 1,6 | 10,0 | 6,4 | 3,6 | 16,2 | 13,3 | 4,2 | 71,9 | 32,5 | 2,7 | 93,6 | 25,4 | 2,7 | 93,6 | 25,4 |
| 2,4 | 31,5 | 12,5 | 2,4 | 18,8 | 11,2 | 2,7 | 93,6 | 25,4 | 1,6 | 10,0 | 6,4 | 2,4 | 31,5 | 12,5 |
| 3,3 | 36,7 | 14,3 | 3,0 | 35,3 | 16,4 | 1,6 | 10,0 | 6,4 | 2,4 | 31,5 | 12,5 | 1,8 | 13,8 | 6,5 |
| 1,8 | 13,8 | 6,5 | 1,8 | 13,8 | 6,5 | 2,4 | 31,5 | 12,5 | 3,3 | 36,7 | 14,3 | 1,6 | 30,4 | 15,8 |
| 2,4 | 64,8 | 22,7 | 2,4 | 64,8 | 22,7 | 3,3 | 36,7 | 14,3 | 1,8 | 13,8 | 6,5 | 0,9 | 31,3 | 18,9 |
| 1,6 | 30,4 | 15.8 | 1,6 | 30,4 | 15,8 | 1,8 | 13,8 | 6,5 | 2,4 | 64,8 | 22,7 | 6,5 | 107,9 | 50,4 |
| 1,4 | 12,1 | 9,3 | 1,4 | 12,1 | 9,3 | 2,4 | 64,8 | 22,7 | 1,6 | 30,4 | 15,8 | 3,6 | 16,2 | 13,3 |
Задачи 16-20
Имеются данные 12 месяцев по району города о рынке вторичного жилья, (у – стоимость квартиры, тыс. у.е., х1 – размер жилой площади, м2, х2 – размер кухни, м2. Данные приведены в табл. 2.4.
Таблица 2.4
| Задача 16 | Задача 17 | Задача 18 | Задача 19 | Задача 20 | ||||||||||
| у | х1 | х2 | у | х1 | х2 | у | х1 | х2 | у | х1 | х2 | у | х1 | х2 |
| 13,0 | 37,0 | 6,2 | 13,2 | 46,0 | 5,8 | 23,0 | 22,8 | 5,0 | 22,5 | 37,2 | 7,6 | 22,7 | 28,8 | 5,4 |
| 16,4 | 60,9 | 10,0 | 15,9 | 54,1 | 8,5 | 26,8 | 27,7 | 5,2 | 25,5 | 58,0 | 9,4 | 25,8 | 36,2 | 7,2 |
| 17,0 | 60,0 | 8,5 | 16,2 | 50,6 | 8,0 | 28,0 | 34,5 | 6,0 | 19,2 | 60,2 | 9,5 | 20,8 | 28,9 | 5,6 |
| 15,2 | 52,1 | 7,4 | 15,4 | 43,8 | 5,2 | 18,4 | 26,4 | 5,1 | 13,6 | 52,0 | 8,1 | 15,2 | 32,4 | 6,4 |
| 14,2 | 40,1 | 7,0 | 14,2 | 78,6 | 12,0 | 30,4 | 19,8 | 4,8 | 25,4 | 44,6 | 7,4 | 25,4 | 49,7 | 7,5 |
| 10,5 | 30,4 | 6,2 | 11,0 | 60,2 | 7,2 | 20,8 | 17,9 | 4,5 | 17,8 | 31,2 | 6,3 | 19,4 | 38,1 | 6,7 |
| 20,0 | 43,0 | 7,5 | 21,1 | 50,2 | 7,0 | 22,4 | 25,2 | 5,4 | 18,0 | 26,4 | 5,9 | 18,2 | 30,2 | 6,2 |
| 12,0 | 32,1 | 6,4 | 13,4 | 54,7 | 7,3 | 21,8 | 20,4 | 4,9 | 21,1 | 20,7 | 5,5 | 21,0 | 32,6 | 6,4 |
| 15,6 | 35,1 | 7,0 | 15,6 | 42,8 | 5,5 | 18,5 | 20,7 | 5,0 | 16,5 | 22,4 | 5,7 | 16,4 | 27,5 | 5,5 |
| 12,5 | 32,0 | 6,2 | 12,8 | 60,4 | 7,3 | 23,5 | 21,4 | 5,2 | 23,0 | 35,4 | 6,8 | 23,5 | 39,0 | 6,9 |
| 13,2 | 33,0 | 6,0 | 14,5 | 47,2 | 5,8 | 16,7 | 19,6 | 4,5 | 16,2 | 28,4 | 6,5 | 18,8 | 27,5 | 5,4 |
| 14,6 | 32,5 | 5,8 | 15,1 | 40,6 | 5,2 | 20,4 | 24,5 | 4,9 | 17,2 | 22,7 | 6,0 | 17,5 | 31,2 | 6,3 |
Задание:
1. Рассчитайте параметры линейного уравнения множественной регрессии.
2. Дайте оценку силы связи факторов с результатом с помощью средних коэффициентов эластичности.
3. Оцените статистическую зависимость параметров и уравнения регрессии в целом с помощью соответственно критериев Стьюдента и Фишера (α=0,01).
4. Рассчитайте среднюю ошибку аппроксимации. Сделайте вывод.
5. Составьте матрицы парных и частных коэффициентов корреляции и укажите информативные факторы.
6. Оцените полученные результаты, выводы оформите в аналитической записке.
Задание 3
Системы эконометрических уравнений
Сложные экономические процессы описывают с помощью системы взаимосвязанных (одновременных) уравнений (СОУ), в которых одни и те же переменные в различных регрессионных уравнениях могут одновременно выступать и в роли результирующих показателей, и в роли объясняющих переменных.
Различают несколько видов систем уравнений:
- системы независимых уравнений – когда каждая зависимая переменная  рассматривается как функция одного и того же набора факторов
рассматривается как функция одного и того же набора факторов  :
:
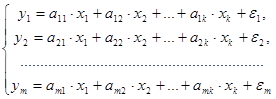
Для решения этой системы и нахождения ее параметров используется метод наименьших квадратов (МНК);
- системы рекурсивных уравнений – когда зависимая переменная  одного уравнения выступает в виде фактора в другом уравнении:
одного уравнения выступает в виде фактора в другом уравнении:

Для решения этой системы и нахождения ее параметров используется метод наименьших квадратов;
- система совместных уравнений – когда одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других – в правую:
 (3.1)
(3.1)
Такая система уравнений называется структурной формой модели.
Эндогенные переменные – взаимозависимые переменные, которые определяются внутри модели (системы)  .
.
Экзогенные переменные – независимые переменные, которые определяются вне системы  .
.
Предопределенные переменные – экзогенные и лаговые (за предыдущие моменты времени) эндогенные переменные системы.
Коэффициенты 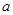 и
и  при переменных – структурные коэффициенты модели.
при переменных – структурные коэффициенты модели.
Система линейных функций эндогенных переменных от всех предопределенных переменных системы – приведенная форма модели:

 (3.2)
(3.2)
где  - коэффициенты приведенной формы модели.
- коэффициенты приведенной формы модели.
Параметры приведенной системы могут быть оценены МНК. Оценки, полученные методом наименьших квадратов, могут быть использованы для оценивания структурных параметров (косвенный метод наименьших квадратов (КМНК)).
При этом возможны следующие ситуации:
- однозначное выражение структурных коэффициентов через коэффициенты приведенной модели – идентифицируемость уравнения;
- структурный коэффициент допускает несколько различных оценок КМНК сверхидентифицируемость уравнения;
- структурный коэффициент не может быть выражен через коэффициенты приведенной модели – неидентифицируемость уравнения.
Необходимое условие идентификации – выполнение счетного правила:
 – уравнение идентифицируемо;
– уравнение идентифицируемо;
 – уравнение неидентифицируемо;
– уравнение неидентифицируемо;
 – уравнение сверхидентифицируемо,
– уравнение сверхидентифицируемо,
где  – число эндогенных переменных в уравнении,
– число эндогенных переменных в уравнении,
 – число предопределенных переменных, отсутствующих в уравнении, но присутствующих в системе.
– число предопределенных переменных, отсутствующих в уравнении, но присутствующих в системе.
Достаточное условие идентификации – определитель матрицы, составленной из коэффициентов при переменных, присутствующих в исследуемом уравнении, не равен нулю, а ранг этой матрицы не менее числа эндогенных переменных системы без единицы.
Для решения идентифицируемого уравнения применяется косвенный метод наименьших квадратов, для решения сверхидентифицированных и неидентифицированных – двухшаговый метод наименьших квадратов.
Косвенный МНК состоит в следующем:
- составляют приведенную форму модели и определяют числовые значения параметров каждого ее уравнения обычным МНК;
- путем алгебраических преобразований переходят от приведенной формы к уравнениям структурной формы модели, получая тем самым численные оценки структурных параметров.
Двухшаговый МНК заключается в следующем:
- составляют приведенную форму модели и определяют численные значения параметров каждого его уравнения обычным МНК;
- выявляют эндогенные переменные, находящиеся в правой части структурного уравнения, параметры которого определяют двухшаговым МНК, и находят расчетные значения по соответствующим уравнениям приведенной формы модели;
- обычным МНК определяют параметры структурного уравнения, используя в качестве исходных данных фактические значения предопределенных переменных и расчетные значения эндогенных переменных, стоящих в правой части данного структурного уравнения.
Замечание. Если в модели есть тождества, то их исключают перед статистическими исследованиями.
Пример 3. 1. Оценить структурную модель на идентификацию:
y1 = b12y2+a11x1+a12x2,
y2=b21y1+b23y3+a22x2,
y3 = b32y2+a31x1+a33x3.
2. На основе приведенной модели
Y1 = 2x1+4x2+10x3,
Y2=3x1-6x2+2x3,
Y3 = -5x1+8x2+5x3.
Найти структурные коэффициенты модели.
1. Модель имеет три эндогенные (у1у2у3) и три экзогенные переменные (х1х2х3).
Проверим необходимое условие идентификации:
1-е уравнение: D=1 (x3), H=2 (у1,у2), D+1=H - уравнение идентифицировано.
2-е уравнение: D=2 (х1,х3), H=3 (у1,у2,у3), D+1=H - уравнение идентифицировано.
3-е уравнение: D=1 (x2), H=2 (у2,у3), D+1=H - уравнение идентифицировано.
Следовательно, необходимое условие идентифицируемости выполнено.
Проверим достаточное условие:
В первом уравнении нет переменных х3, у3
Строим матрицу:
| Х3 | У3 | |
| 2 ур. | 0 | b23 |
| 3 ур. | а33 | -1 |
det M = det  , rank M =2.
, rank M =2.
Во втором уравнении нет переменных х1, х3
Строим матрицу:
| Х3 | У3 | |
| 1 ур. | а11 | 0 |
| 3 ур. | а31 | а33 |
det M = det  , rank M =2.
, rank M =2.
В третьем уравнении нет переменных у1, х2
Строим матрицу:
| Х3 | У3 | |
| 1 ур. | -1 | а12 |
| 2 ур. | b21 | a22 |
det M = det  , rank M =2.
, rank M =2.
Следовательно, достаточное условие идентифицируемости выполнено.
Система точно идентифицируема.
2. Найдем структурные коэффициенты модели.
Для этого:
Запишем систему (3.1) в матричной форме, перенеся все эндогенные переменные в левые части системы:
y1-b12y2=a11x1+a12x2,
-b21y1+y2-b23y3=a22x2,
-b32y2+y3=a31x1+a33x3.
откуда  , и
, и  ,
,  ,
,  ,
,  .
.
Решаем систему относительно  :
:  . Найдем
. Найдем
 , где
, где  – алгебраические дополнения соответствующих элементов матрицы
– алгебраические дополнения соответствующих элементов матрицы  ,
,  – минор, т.е. определитель, полученный из матрицы
– минор, т.е. определитель, полученный из матрицы 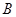 вычеркиванием i-й строки и j-го столбца.
вычеркиванием i-й строки и j-го столбца.
 ,
,
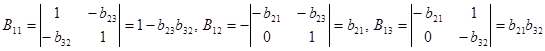 ,
,
 ,
,
 .
.
Поэтому

Сравнивая полученную систему с системой (3.2), получим систему из 9 уравнений с 9 неизвестными, после решения которой находим коэффициенты структурной формы.
В данном случае эти коэффициенты можно найти значительно проще. Находим  из второго уравнения приведенной системы (3.2) и подставим его в первое уравнение этой системы. Тогда первое уравнение системы (3.1) примет вид:
из второго уравнения приведенной системы (3.2) и подставим его в первое уравнение этой системы. Тогда первое уравнение системы (3.1) примет вид:  , откуда
, откуда 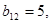
 ,
,  . Из третьего уравнения системы (3.2) находим
. Из третьего уравнения системы (3.2) находим  и подставляем во второе уравнение системы, получим:
и подставляем во второе уравнение системы, получим:  , решая его совместно с уравнением
, решая его совместно с уравнением  и, исключая
и, исключая  , получим
, получим  . Сравнивая это уравнение со вторым уравнением системы (3.1), получим
. Сравнивая это уравнение со вторым уравнением системы (3.1), получим  . Выражая
. Выражая  из второго уравнения, и подставляя в третье системы (3.2), получим
из второго уравнения, и подставляя в третье системы (3.2), получим  . Сравнивая это уравнение с третьим уравнением системы (3.1), получим
. Сравнивая это уравнение с третьим уравнением системы (3.1), получим  .
.
КОНТРОЛЬНОЕ ЗАДАНИЕ № 3
Задание к задачам 21 - 30:
1. Используя необходимое и достаточное условие идентификации, определить, идентифицировано ли каждое уравнение модели.
2. Определите тип модели.
3. Определите метод оценки параметров модели.
4. Опишите последовательность действий при использовании указанного метода.
5. Результаты оформите в виде пояснительной записки.
Задача 21
Гипотетическая модель экономики:
Сt = a1+b11Yt+b12Yt+e1,
Jt = a2+b21Yt-1+e2,
Tt = a3+b31Yt+e3,
Gt = Сt+ Yt,
где Сt – совокупное потребление в период t:
Yt – совокупный доход в период t;
Jt – инвестиции в период t;
Tt – налоги в период t;
Gt – государственные доходы в период t.
Задача 22
Модель спроса и предложения на деньги:
Rt = a1+b11Mt+b12Yt+e1,
Yt = a2+b21Rt+e2,
где R – процентные ставки в период t;
Y – ВВП в период t;
М – денежная масса в период t.
Задача 23
Макроэкономическая модель:
Сt = a1+b12Yt+b13Тt+e1,
It = a2+b21Yt+ b24Kt-1+e1,
Yt = Сt+It,
где С – потребление;
I – инвестиции;
Y – доход;
T – налоги;
K – запас капитала.
Задача 24
Модель денежного и товарного рынков:
Rt = a1+b12Yt+b14Mt+e1,
Yt = a2+b21Rt+ b23It+ b25Gt+e2,
It = a3+b31Rt+e3,
где R – процентные ставки;
Y – реальный ВВП;
M – денежная масса;
I – внутренние инвестиции;
G – реальные государственные расходы.
Задача 25
Модель денежного рынка:
Rt = a1+b11Mt+b12Yt+e1,
Yt = a2+b21Rt+ b22It +e2,
It = a3+b33Rt+e1,
где R – процентные ставки;
Y – ВВП;
M – денежная масса;
I – внутренние инвестиции/
Задача 26
Модель имеет вид:
Y1 = a1+b12Y2+e1,
Y2 = a2+b21Y1+ C21X1 +e2,
Y3 = Y1+ X2.
Задача 27
Модель имеет вид:
Y1 = a1+b11X1+ b12X2+C12Y2+e1,
Y2 = a2+b22X2+ C21Y1 +e2,
Y3 = a3+b31X1 + b33X3+e3.
Задача 28
Модель имеет вид:
Y1 = a1+b11X1+ b13X3+C12Y2+e1,
Y2 = a2+b22X2+ C21Y1 +e2,
Y3 = a3+b32X2 + b33X3+e3.
Задача 29
Модель имеет вид:
Y1 = b12Y2+a11X1+a12X2+e1,
Y2 = b21Y1+b23Y3+a22X2+e2,
Y3 = b31Y1+a31X1+a33X3+e3.
Задача 30
Модель имеет вид:
Y1 = b12Y2+a11X1+a12X2+e1,
Y2 = b21Y1+a22X2+a23X3+e2,
Y3 = b31Y1+a33X3+e3.
Задание 4
Анализ временных рядов
Модели, построенные по данным, характеризующим один объект за ряд последовательных моментов (периодов), называется моделями временных рядов.
Временной ряд – это совокупность значений какого-либо показателя за несколько последовательных моментов или периодов.
Каждый уровень временного ряда формируется из трендовой (Т), циклической ( S ), случайной ( E ) компонент.
Модели, в которых временной ряд представлен как сумма перечисленных компонент, - аддитивные модели, как произведение – мультипликативные модели временного ряда.
Аддитивная модель имеет вид:  ;
;
Мультипликативная модель:  .
.
Построение аддитивной и мультипликативной моделей сводится к расчету значений  и
и  для каждого уровня ряда.
для каждого уровня ряда.
Построение модели включает в себя следующие шаги:
1) выравнивание исходного ряда методом скользящей средней;
2) расчет значений сезонной компоненты  ;
;
3) устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных в аддитивной  или в мультипликативной
или в мультипликативной  модели.
модели.
4) аналитическое выравнивание уровней  или
или  и расчет значений Е с использованием полученного уравнения тренда;
и расчет значений Е с использованием полученного уравнения тренда;
5) расчет полученных по модели значений  или
или  ;
;
6) расчет абсолютных и (или) относительных ошибок.
Автокорреляцией уровней ряда – это корреляционная зависимость между последовательными уровнями временного ряда:
 , (4.1)
, (4.1)
где  ;
;  – коэффициент автокорреляции уровней ряда
– коэффициент автокорреляции уровней ряда
первого порядка;
 , (4.2)
, (4.2)
где 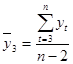 ;
;  – коэффициент автокорреляции уровней ряда второго порядка.
– коэффициент автокорреляции уровней ряда второго порядка.
Формулы для расчета коэффициентов автокорреляции старших порядков легко получить из формулы линейного коэффициента корреляции.
Последовательность коэффициентов автокорреляции уровней первого, второго и т.д. порядков называют автокорреляционной функцией временного ряда, а график зависимости ее значений от величины лага (порядка коэффициента автокорреляции) – коррелограммой.
Построение аналитической функции для моделирования тенденции (тренда) временного ряда называют аналитическим выравниванием временного ряда. Для этого чаще всего применяются следующие функции:
- линейная  ;
;
- гипербола  :
:
- экспонента  ;
;
- степенная функция  ;
;
- парабола второго и более высоких порядков 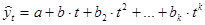 .
.
Параметры трендов определяются обычным МНК, в качестве независимой переменной выступает время  , а в качестве зависимой переменной – фактические уровни временного ряда
, а в качестве зависимой переменной – фактические уровни временного ряда  . Критерием отбора наилучшей формы тренда является наибольшее значение скорректированного коэффициента детерминации
. Критерием отбора наилучшей формы тренда является наибольшее значение скорректированного коэффициента детерминации  .
.
Автокорреляция в остатках – корреляционная зависимость между значениями остатков  за текущий и предыдущие моменты времени.
за текущий и предыдущие моменты времени.
Для определения автокорреляции остатков используют критерий Дарбина – Уотсона и расчет величины:
 .
.
ПРИМЕР 4. Имеются данные об урожайности овощных культур в хозяйствах региона. Данные приведены в табл. 4.1.
Таблица 4.1
| Год | 1989 | 1990 | 1991 | 1992 | 1993 | 1994 | 1995 | 1996 |
| Урожайность, т/га | 10,2 | 10,7 | 11,7 | 13.1 | 14,9 | 17,2 | 20,0 | 23,2 |
Для данного временного ряда требуется:
1. Обосновать тип уравнения тренда.
2. Рассчитать параметры тренда.
3. Дать прогноз на 1997 год.
Решение. Определим коэффициент корреляции между рядами  и
и  . Воспользуемся формулой (4.1), расчеты приведены в таблице 4.2:
. Воспользуемся формулой (4.1), расчеты приведены в таблице 4.2:

Таблица 4.2
|
| год | 
| 
| 
| 
| 
| 
| 
| 
| 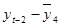
| 
| 
| 
| 
|
| 1 | 10,2 | - | - | - | - | - | - | - | - | - | - | - | - | |
| 2 | 10,7 | 10,2 | - | -5,128 | -3,771 | 26,2964 | 14,22044 | - | - | - | - | 19,33769 | - | |
| 3 | 11,7 | 10,7 | 10,2 | -4,128 | -3,271 | 17,0404 | 10,69944 | -4,983 | -2,767 | 24,83029 | 7,656289 | 13,50269 | 13,78796 | |
| 4 | 13,1 | 11,7 | 10,7 | -2,728 | -2,271 | 7,44198 | 5,157441 | -3,583 | -2,267 | 12,83789 | 5,139289 | 6,195288 | 8,122661 | |
| 5 | 14,9 | 13,1 | 11,7 | -0,928 | -0,871 | 0,86118 | 0,758641 | -1,783 | -1,267 | 3,179089 | 1,605289 | 0,808288 | 2,259061 | |
| 6 | 17,2 | 14,9 | 13,1 | 1,372 | 0,929 | 1,88238 | 0,863041 | 0,517 | 0,133 | 0,267289 | 0,017689 | 1,274588 | 0,068761 | |
| 7 | 20,0 | 17,2 | 14,9 | 4,172 | 3,229 | 17,4056 | 10,42644 | 3,317 | 1,933 | 11,00249 | 3,736489 | 13,47139 | 6,411761 | |
| 8 | 23,2 | 20,0 | 17,2 | 7,372 | 6,029 | 54,2464 | 36,34884 | 6,517 | 4,233 | 42,47129 | 17,91829 | 44,44579 | 27,58646 | |

| 36 | 0,004 | 0,003 | 125,274 | 78,47429 | 0,002 | -0,002 | 94,58833 | 36,07333 | 99,03572 |  58,23667 58,23667
| |||
| Средн. | 4,5 | 
| 
| 
|
Результат говорит о тесной зависимости между урожайностью текущего и непосредственно предшествующего годов и наличии во временном ряде сильной линейной тенденции.
Определим коэффициент автокорреляции второго порядка по формуле (4.2):
 ,
, 
Результат подтверждает наличие линейной тенденции. Выбираем линейное уравнение тренда:  .
.
3. Параметры определим, используя МНК. Результаты расчетов приведены в табл. 4.3.
Таблица 4.3
|
| 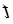
| 
| 
| 
| 
| 
| 
| 
| 
| 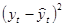
|
| 1 | 10,2 | 1 | 104,04 | 10,2 | -3,5 | 12,25 | 8,800 | 1,400 | 1,960 | |
| 2 | 10,7 | 4 | 114,49 | 21,4 | -2,5 | 6,25 | 10,607 | 0,093 | 0,009 | |
| 3 | 11,7 | 9 | 136,89 | 35,1 | -1,5 | 2,25 | 12,414 | -0,714 | 0,09 | |
| 4 | 13,1 | 16 | 171,61 | 52,4 | -0,5 | 0,25 | 14,221 | -1,121 | 1,257 | |
| 5 | 14,9 | 25 | 222,01 | 72,5 | 0,5 | 0,25 | 16,028 | -1,128 | 1,272 | |
| 6 | 17,2 | 36 | 295,84 | 103,2 | 1,5 | 2,25 | 17,835 | -0,635 | 0,403 | |
| 7 | 20,0 | 49 | 400,00 | 140 | 2,5 | 6,25 | 19,642 | 0,358 | 0,128 | |
| 8 | 23,2 | 64 | 538,24 | 185,5 | 3,5 | 12,25 | 21,449 | 1,751 | 3,066 | |

| 36 | 121 | 204 | 1983,12 | 620,4 | 0,00 | 32,00 | 8,604 | ||
| Средн. | 4,5 | 15,125 | 25,5 | 247,890 | 77,55 |
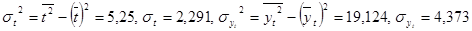
 .
.
Уравнение тренда примет вид:  , коэффициент корреляции
, коэффициент корреляции 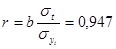 .
.
Расчетное значение критерия Фишера равно  ,
,  , следовательно, уравнение статистически значимо и прогноз имеет смысл.
, следовательно, уравнение статистически значимо и прогноз имеет смысл.
Прогнозное значение (при  ),
),  , средняя ошибка прогноза вычислим по формуле
, средняя ошибка прогноза вычислим по формуле
 , где остаточная дисперсия
, где остаточная дисперсия  рассчитывается по формуле
рассчитывается по формуле
 ;
;  .
.
Предельная ошибка прогноза  ,
,
 ,
,  .
.
Доверительный интервал прогноза  .
.
Выполненный прогноз надежный и достаточно точный. Следовательно, применительно к рассмотренному временному ряду темпы роста урожайности за восемь рассмотренных лет изменялись от 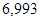 (т/га) со средним за год приростом, равным
(т/га) со средним за год приростом, равным  (т/га).
(т/га).
КОНТРОЛЬНОЕ ЗАДАНИЕ № 4
Задачи 31-35
Имеются данные за пятнадцать дней по количеству пациентов клиники, прошедших через соответствующие отделения в течение дня. Данные приведены в табл. 4.4.
Таблица 4.4
|
День | Задача 31 | Задача 32 | Задача 33 | Задача 34 | Задача 35 |
| Терапевти-ческое отделение | Хирургичес-кое отделение | Стоматологическое отделение | Глазное отделение | Отделение пласти-ческой хирургии | |
| 1 | 29 | 35 | 41 | 30 | 22 |
| 2 | 40 | 29 | 52 | 22 | 19 |
| 3 | 30 | 22 | 30 | 19 | 11 |
| 4 | 52 | 19 | 47 | 28 | 12 |
| 5 | 47 | 30 | 28 | 24 | 16 |
| 6 | 28 | 47 | 22 | 18 | 28 |
| 7 | 16 | 28 | 51 | 35 | 30 |
| 8 | 51 | 12 | 40 | 29 | 18 |
| 9 | 40 | 13 | 57 | 40 | 17 |
| 10 | 35 | 15 | 33 | 34 | 20 |
| 11 | 57 | 18 | 43 | 31 | 21 |
| 12 | 28 | 19 | 51 | 29 | 19 |
| 13 | 33 | 20 | 36 | 35 | 24 |
| 14 | 42 | 16 | 19 | 23 | 13 |
| 15 | 39 | 35 | 42 | 27 | 16 |
Задачи 36-40
Имеются данные за двенадцать лет по странам о годовом объеме продаж автомобилей. Данные приведены в табл. 4.5.
Таблица 4.5
| Год Объем продаж 100 тыс. | Задача 36 | Задача 37 | Задача 38 | Задача 39 | Задача 40 |
| Страна А | Страна В | Страна С | Страна Д | Страна Е | |
| 1986 | 3,8 | 4,1 | 5,2 | 2,8 | 4,2 |
| 1987 | 4,7 | 5,2 | 6,3 | 3,6 | 5,4 |
| 1988 | 3,9 | 4,3 | 4,5 | 2,7 | 4,0 |
| 1989 | 2,7 | 3,2 | 3,9 | 2,0 | 3,1 |
| 1990 | 2,9 | 3,0 | 3,8 | 1,8 | 2,9 |
| 1991 | 2,3 | 2,8 | 3,0 | 1,4 | 2,4 |
| 1992 | 3,0 | 4,2 | 4,8 | 2,1 | 3,7 |
| 1993 | 3,6 | 4,6 | 5,0 | 2,5 | 4,1 |
| 1994 | 2,9 | 3,7 | 4.6 | 2,1 | 1,4 |
| 1995 | 3,7 | 4,8 | 6,1 | 3,0 | 2,2 |
| 1996 | 4,5 | 5,6 | 6,7 | 3,7 | 2,9 |
| 1997 | 4,2 | 5,0 | 6,9 | 3,1 | 2,6 |
Требуется:
1. Определить коэффициенты автокорреляции уровней ряда первого и второго порядка.
2. Обосновать выбор уравнения тренда и определите его параметры.
3. Сделать выводы.
4. Результаты оформить в виде пояснительной записки.
Библиографический список
1. Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы эконометрики. – М.: ЮНИТИ, 1998.
2. Катышев П.К., Пересецкий А.А. Сборник задач к начальному курсу эконометрики. – М.: Дело, 1999.
3. Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика: начальный курс. – М.: Дело, 2000.
4. Практикум по эконометрике. Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2001.
5. Эддоус М., Стэнсфилд Р. Методы принятия решения. – М.: ЮНИТИ, 1997.
6. Эконометрика. Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2001.
Приложение 1
Таблица значений F -критерия Фишера при уровне значимости

 
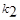
| 1 | 2 | 3 | 4 | 5 | 6 | 8 | 12 | 24 | 
|
| 1 | 161,45 | 199,50 | 215,72 | 224,57 | 230,17 | 233,97 | 238,89 | 243,91 | 249,04 | 234,52 |
| 2 | 18,51 | 19,00 | 19,16 | 19,25 | 19,30 | 19,33 | 19,37 | 19,41 | 19,45 | 19,50 |
| 3 | 10,13 | 9,55 | 9,28 | 9,12 | 9,01 | 8,94 | 8,84 | 8,74 | 8,64 | 8,53 |
| 4 | 7,71 | 6,94 | 6,59 | 6,39 | 6,26 | 6,16 | 6,04 | 5,91 | 5,77 | 5,63 |
| 5 | 6,61 | 5,79 | 5,41 | 5,19 | 5,05 | 4,95 | 4,82 | 4,68 | 4,53 | 4,36 |
| 6 | 5,99 | 5,14 | 4,76 | 4,53 | 4,39 | 4,28 | 4,15 | 4,00 | 3,84 | 3,67 |
| 7 | 5,59 | 4,74 | 4,35 | 4,12 | 3,97 | 3,87 | 3,73 | 3,57 | 3,41 | 3,23 |
| 8 | 5,32 | 4,46 | 4,07 | 3,84 | 3,69 | 3,58 | 3,44 | 3,28 | 3,12 | 2,93 |
| 9 | 5,12 | 4,26 | 3,86 | 3,63 | 3,48 | 3,37 | 3,23 | 3,07 | 2,90 | 2,71 |
| 10 | 4,96 | 4,10 | 3,71 | 3,48 | 3,33 | 3,22 | 3,07 | 2,91 | 2,74 | 2,54 |
| 11 | 4,84 | 3,98 | 3,59 | 3,36 | 3,20 | 3,09 | 2,95 | 2,79 | 2,61 | 2,40 |
| 12 | 4,75 | 3,88 | 3,49 | 3,26 | 3,11 | 3,00 | 2,85 | 2,69 | 2,50 | 2,30 |
| 13 | 4,67 | 3,80 | 3,41 | 3,18 | 3,02 | 2,92 | 2,77 | 2,60 | 2,42 | 2,21 |
| 14 | 4,60 | 3,74 | 3,34 | 3,11 | 2,96 | 2,85 | 2,70 | 2,53 | 2,35 | 2,13 |
| 15 | 4,54 | 3,68 | 3,29 | 3,06 | 2,90 | 2,79 | 2,64 | 2,48 | 2,29 | 2,07 |
| 16 | 4,49 | 3,63 | 3,24 | 3,01 | 2,85 | 2,74 | 2,59 | 2,42 | 2,24 | 2,01 |
| 17 | 4,45 | 3,59 | 3,20 | 2,96 | 2,81 | 2,70 | 2,55 | 2,38 | 2,19 | 1,96 |
| 18 | 4,41 | 3,55 | 3,16 | 2,93 | 2,77 | 2,66 | 2,51 | 2,34 | 2,15 | 1,92 |
| 19 | 4,38 | 3,52 | 3,13 | 2,90 | 2,74 | 2,63 | 2,48 | 2,31 | 2,11 | 1,88 |
| 20 | 4,35 | 3,49 | 3,10 | 2,87 | 2,71 | 2,60 | 2,45 | 2,28 | 2,08 | 1,84 |
| 21 | 4,32 | 3,47 | 3,07 | 2,84 | 2,68 | 2,57 | 2,42 | 2,25 | 2,05 | 1,81 |
| 22 | 4,30 | 3,44 | 3,05 | 2,82 | 2,66 | 2,55 | 2,40 | 2,23 | 2,03 | 1,78 |
| 23 | 4,28 | 3,42 | 3,03 | 2,80 | 2,64 | 2,53 | 2,38 | 2,20 | 2,00 | 1,76 |
| 24 | 4,26 | 3,40 | 3,01 | 2,78 | 2,62 | 2,51 | 2,36 | 2,18 | 1,98 | 1,73 |
| 25 | 4,24 | 3,38 | 2,99 | 2,76 | 2,60 | 2,49 | 2,34 | 2,16 | 1,96 | 1,71 |
| 26 | 4,22 | 3,37 | 2,98 | 2,74 | 2,59 | 2,47 | 2,32 | 2,15 | 1,95 | 1,69 |
| 27 | 4,21 | 3,35 | 2,96 | 2,73 | 2,57 | 2,46 | 2,30 | 2,13 | 1,93 | 1,67 |
| 28 | 4,20 | 3,34 | 2,95 | 2,71 | 2,56 | 2,44 | 2,29 | 2,12 | 1,91 | 1,65 |
| 29 | 4,18 | 3,33 | 2,93 | 2,70 | 2,54 | 2,43 | 2,28 | 2,10 | 1,90 | 1,64 |
| 30 | 4,17 | 3,32 | 2,92 | 2,69 | 2,53 | 2,42 | 2,27 | 2,09 | 1,89 | 1,62 |
| 35 | 4,12 | 3,26 | 2,87 | 2,64 | 2,48 | 2,37 | 2,22 | 2,04 | 1,83 | 1,57 |
| 40 | 4,08 | 3,23 | 2,84 | 2,61 | 2,45 | 2,34 | 2,18 | 2,00 | 1,79 | 1,51 |
| 45 | 4,06 | 3,21 | 2,81 | 2,58 | 2,42 | 2,31 | 2,15 | 1,97 | 1,76 | 1,48 |
| 50 | 4,03 | 3,18 | 2,79 | 2,56 | 2,40 | 2,29 | 2,13 | 1,95 | 1,74 | 1,44 |
| 60 | 4,00 | 3,15 | 2,76 | 2,52 | 2,37 | 2,25 | 2,10 | 1,92 | 1,70 | 1,39 |
| 70 | 3,98 | 3,13 | 2,74 | 2,50 | 2,35 | 2,23 | 2,07 | 1,89 | 1,67 | 1,35 |
| 80 | 3,96 | 3,11 | 2,72 | 2,49 | 2,33 | 2,21 | 2,06 | 1,88 | 1,65 | 1,31 |
| 90 | 3,95 | 3,10 | 2,71 | 2,47 | 2,32 | 2,20 | 2,04 | 1,86 | 1,65 | 1,31 |
| 100 | 3,94 | 3,09 | 2,70 | 2,46 | 2,30 | 2,19 | 2,03 | 1,85 | 1,63 | 1,26 |
| 125 | 3,92 | 3,07 | 2,68 | 2,44 | 2,29 | 2,17 | 2,01 | 1,83 | 1,60 | 1,21 |
| 150 | 3,90 | 3,06 | 2,66 | 2,43 | 2,27 | 2,16 | 2,00 | 1,82 | 1,59 | 1,18 |
| 200 | 3,89 | 3,04 | 2,65 | 2,42 | 2,26 | 2,14 | 1,98 | 1,80 | 1,57 | 1,14 |
| 300 | 3,87 | 3,03 | 2,64 | 2,41 | 2,25 | 2,13 | 1,97 | 1,79 | 1,55 | 1,10 |
| 400 | 3,86 | 3,02 | 2,63 | 2,40 | 2,24 | 2,12 | 1,96 | 1,78 | 1,54 | 1,07 |
| 500 | 3,86 | 3,01 | 2,62 | 2,39 | 2,23 | 2,11 | 1,96 | 1,77 | 1,54 | 1,06 |
| 1000 | 3,85 | 3,00 | 2,61 | 2,38 | 2,22 | 2,10 | 1,95 | 1,76 | 1,53 | 1,03 |
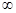
| 3,84 | 2,99 | 2,60 | 2,37 | 2,21 | 2,09 | 1,94 | 1,75 | 1,52 | 1,00 |
Приложение 2
Дата добавления: 2019-02-12; просмотров: 545; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
