Ионическая, коринфская и сложная колонны
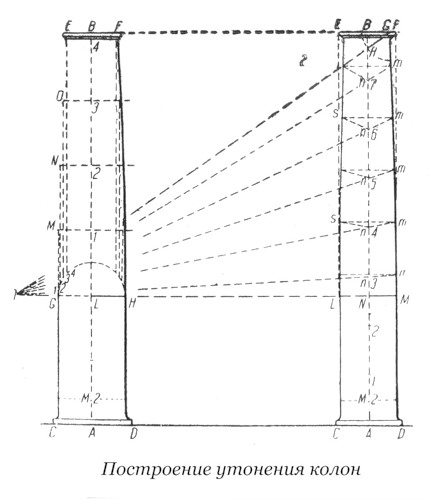
§ Ось колонны делим на 8 частей и к точке N, находящейся на расстоянии 1/3 высоты колонны, проводим произвольной длины горизонтальную линию.
§ Радиусом, равным 1 м., из точки F описываем дугу; от точки F мы проводим через H прямую линию и получаем точку O.
§ Из точки O через точки пересечения на оси проводятся радиусы (лучи), ограниченные точками m, на расстоянии 1 м. от N, 3, 4, 5 и т.д.
§ Из точки m провести горизонтальные плоскости, ограниченные точками s на расстоянии 1 м. от 3, 4, 5 и т.д.
§ Через точки m и s провести линию, которая будет закругленные профилем колонны.
Витая колонна
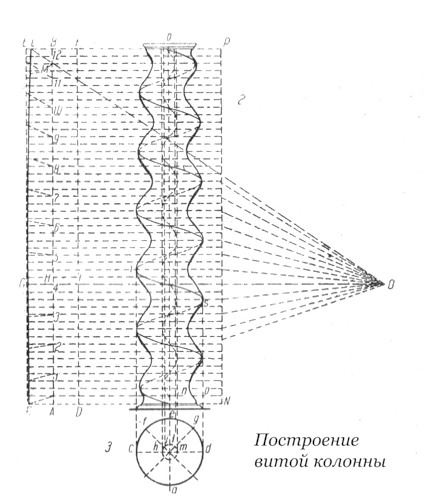
§ Для построения витой колонны необходимо предварительно подготовить в линиях формы колонны, которую желательно изобразить.
§ Посредством стержня обыкновенной колонны применяя второй способ построения утонения, делим ось на 48 равных частей; из полученных точек проводим пунктирные линии, параллельные линии OG.
§ На оси ab вычерчиваем окружность, диаметром, равным выступу колонны, и такую же окружность на линии no.
§ Делим окружность на 8 равных частей, в результате чего получаемточки h, i, e, m; из этих точек проводим вертикальные линии, параллельные оси ab, которые послужат для начертания внешней спирали.
§ Затем нанесем (пользуясь спиралью в горизонтальном положении как осью) соответствующие размеры подготовительной колонны и получим точки, через которые пройдут две вогнутые линии витой колонны.
|
|
|
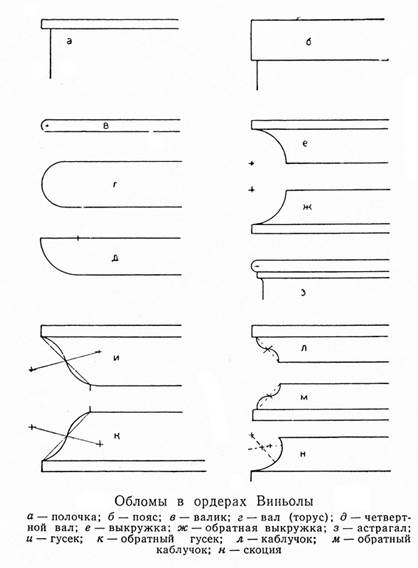
Построение архитектурных обломов
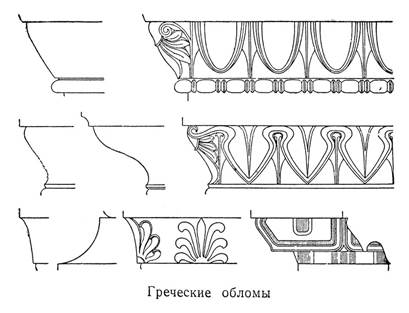
Обломы или мулюры – это простейшие кривые, из которых состоят профили ордера.
Полочка
Полочка– очень малый плоский пояс.
Вал
Вал– профиль, очерченный полуокружностью; в плане – всегда круг.
Валик или астрагал
– малый профиль полукругло-выпуклый или очерченный другой подобной кривой.
Построение
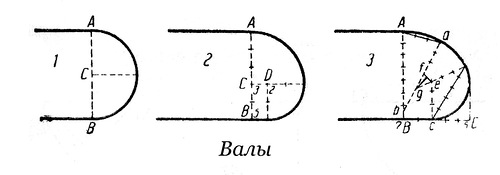
1. АВ = 7 парт. ВС = 5 п.Ab = 6 ½ п. Aa = 3 п. Cc = ce = ed = 3 п.cd = 5 п.аf = 3 п.;
2. Перпендикуляр из середины прямой ef дает точку g, являющуюся центром дуги.
3. Итак, для построения вала (в случае 3) понадобилось 3 центра: точка b для дуги Aa, точка g для дуги ad и точка e для дуги dc.
Выкружка
Выкружка– облом с вогнутой кривой; его применяют для соединения других обломов
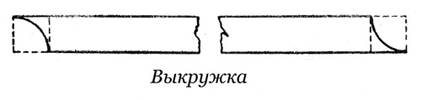
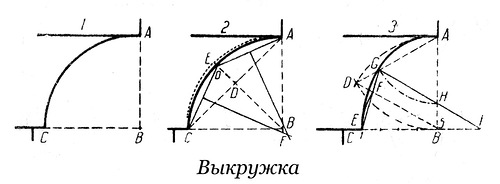
Построение
1. Точка В есть центр дуги AC
2. Перпендикуляр к AC, проходящий через ее середину, дает DE. Точка пересечения O. Пересечение перпендикуляров, проходящих через середины линий oC и оА, в точке F образует центр дуги CoA.
3. ABD равносторонний треугольник; CB делим на 5 равный частей; B – центр дуги EF; прямую EF продолжаем до точки G. Точка A есть центр дуги GH. Прямую GH продолжаем до пересечения с продолжением линии CB в точке I. H – центр дуги AG; I – центр дуги GE.
|
|
|
Четвертной вал
Четвертной вал– облом очерченный четвертью окружности или иной подобной кривой.
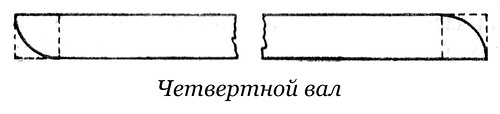
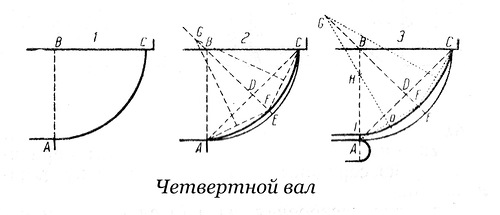
Построение
1. B – центр дуги AC.
2. Перпендикуляр, проходящий через середину AC, есть DE. Точка F – точка пересечения. Перпендикуляры к ½ AF и FC дают точку G – центр дуги AFC.(см. 2). G – центр дуги CFo, H – центр дуги oI.
Гусек
Гусек– волнообразный облом с вогнутой верхней частью и выпуклой нижней.
Построение
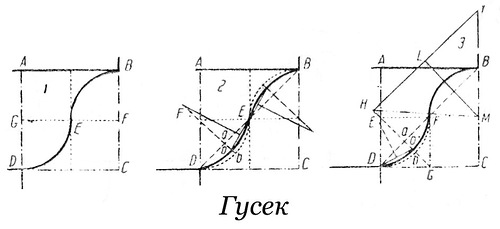
1. 1.2. 3. ABCD есть квадрат.1.2. Квадрат АBCD разделен на 4 равных квадрата.Точки G и F – центры дуг DE и ЕВ.
2. Перпендикуляр, проходящий через середину DE, дает точки a и b. O – точка пересечения. Перпендикуляр к ½ Еo дает точку F – центр дуги EoD.
3. DG есть ½ DC; DEFG есть квадрат; Е – центр дуги FbD; EG – диагональ квадрата; o – точка пересечения.
4. Перпендикуляр c ½ oD дает точку H – центр дуги FoD; Hl параллельна DB; перпендикуляр к ½ Hl дает M – центр дуги FB.
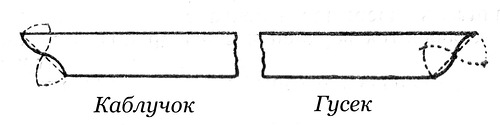
Каблучок
Каблучок– верхняя часть выпуклая, нижняя – вогнутая.
Построение
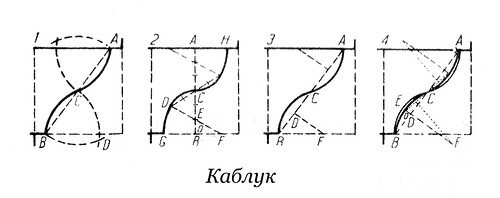
1. 1.2.3. 4. C лежит на ½ АВ.
2. BCD равносторонний, криволинейный треугольник.
3. AB разделим на 6 равных частей; DCE равносторонний треугольник (сторона которого – 2 п.) продолжнение прямой DE дает точку F – центр дуги GD. Точка E – центр дуги DC.
4. Перпендикуляр к ½ BC дает точку Е – центр дуги BC.
|
|
|
5. (см. 1). DE – перпендикуляр, проходящий через середину BC; точка о – точка пересечения. К ½ oC восстанавливаем перпендикуляр; точка пересечения – F; центр дуги CoB.
Скоция
Скоция– профиль в виде “С”, обычно расположен между двумя полочками.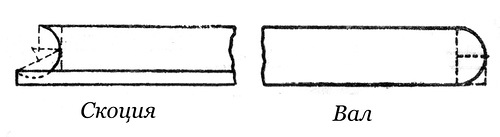 
Построение
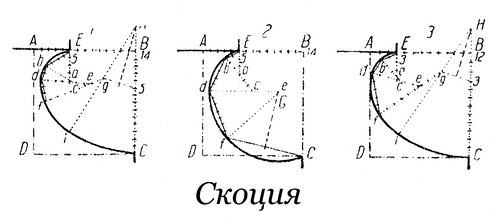
1. AB и BC разделены на 14 п. каждая; 5 ab – равносторонний треугольник со стороной, равной 4 п.; bc = 6 п.; bd = 2 п.; de = 7 п.; df = 3 п.; fg = 9 п. Перпендикуляр к 1 / g 5 дает H центр дуги iC. Итак для построения скоции (случай 1) понадобилось 5 центров: a – для дуги Eb, с – для дуги bd, e – для дуги df, g – для дуги Eb, H – для дуги iC.
2. АB разделим на 14 п. 5а = 3 п.; 5b = 2 п.; be = 6 п.; bd = 5 п.; de = 9 п., df = 7 п. Перпендикуляр к ½ fC дает G – центр дуги fC. Итак, для построения скоции ( случай 2) понадобилось 4 центра: a – для дуги bE; с – для дуги db, e – для дуги df и G – для дуги fC.
3. AB и BC разделим на 12 п. каждая. AE = 3 п.; Ea = 2 ½ п.; Eb = 2 п.; bc = 3 ½ п.; bd = 2 п.; de = 5 ½ п.; df = 5 п.; fg = 9 п. Перпендикуляр к ½ g 3 дает H центр дуги iC.
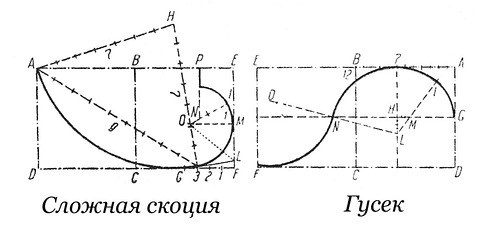
Сложная скоция
Построение
1. ABCD = BDFC; CG есть ½ FC; G3 – ½ GF; АB разделена на 9 п.; AH = H3 = 7 п.: 3L препендикулярно H3. lO биссектриса угла 3LM. O – центр дуги 3MP; Мl = 1 п.; lN = ? п.; Np – перпендикуляр.
2. ABCD = BEFC; BA разделено на 12 п.; G лежит на ½ AD. GH и 7H половины осей овалов (7IG – кривая овала). M – центр дуги IG; L – центр дуги I7N; NO = LN; O – центр дуги NF.
|
|
|
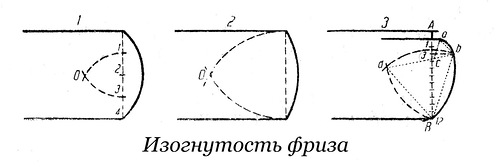
Изогнутость фриза
Построение
1. Высота разделена на 4 части (4 п.); дуги 1-3 дают центр O кривой.
2. Точка О – центр кривой.
3. Высота AB разделена на 12 п.; Al = la = 1 п.; 3b = 2 п.; ab – сторона равностороннего треугольника abc; bB – сторона равностороннего треугольника bBd; c и d – центры дуг ab и bB.
И еще раз)
Каннелюры
Каннелюра – это вертикальный желоб на стволе колонны (такие колонны называют каннелированными, в отличие от гладких), а также горизонтальные желобки на базе колонны ионического ордера. Все классические ордера, кроме тосканского, имеют каннелюры.
Дорическая колонна обрабатывается 20 каннелюрами неглубокого профиля с острыми ребрами (1/3 окружности в плане ), колонные ионического, композитного и коринфского ордеров – 24-мя каннелюрам глубокого профиля (в плане – полукруг), которые разделяются ремешками.
§ Описать полуокружность AB и разделить ее на равные части (10 – 12), проводя радиусы через полученные точки.
§ Радиусом, равным половине одной из частей, из центров в точках 1, 2, 3, 4 и т.д., описать дуги до пересечения с полуокружностью AB; по полученные точками нанести чертеж каннелюр.
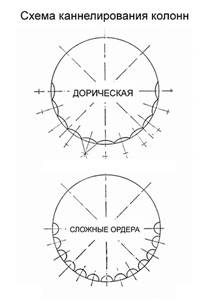
Зубчики (дентикулы)
Дентикулы (дантиклы, зубчики) – ряд небольших прямоугольных кронштейнов, поддерживающих карниз или скат фронтона.
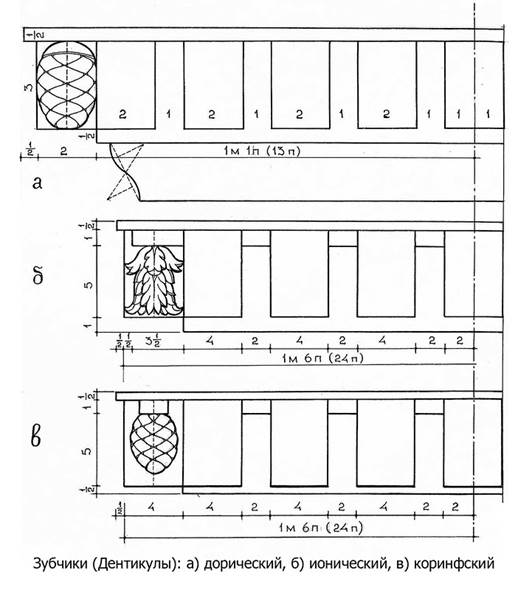
Аттическая база
База, названная Витрувием аттической (книга III, глава 3), созданная афинянами и употребляющаяся до сих пор, применяется в сложном, коринфском, ионическом, дорическом и даже тосканском ордерах; чаще всего она применяется в ионическом ордере, собственный пьедестал которого употребляется значительно реже.
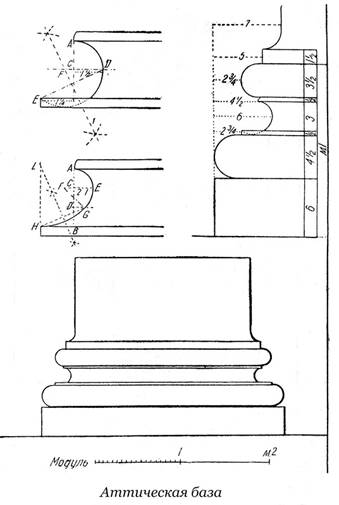
Вионьола, один из создателей сложного ордера, говорил, что он применяет эту базу охотнее, чем все другие.
Независимо от того, что эта база не настолько богата по количеству обломов, как коринфская, она является самой красивой, и ее находят в большом количестве в древности, когда ее применяли, главным образом, к коринфскому ордеру.
Карниз Виньолы
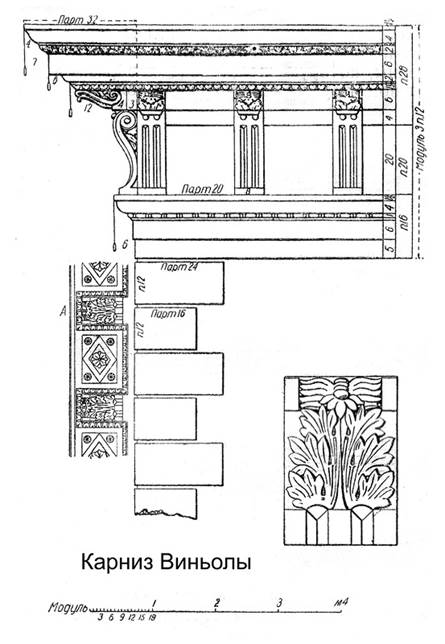
Это одним из самых замечательных как по красоте, так и по композиции, карниз был личным изобретение Виньолы, который часто употреблял его в своих постройках.
Он содержит в себе элементы дорического и коринфского ордеров.
Соотношение частей карнизa
§ Все высота фасада делиться на 11 частей, из которых одна часть принадлежит карнизу, а 10 частей – фасаду.
§ Высота карниза равна 3 м. 12 п.; из них: высота фриза – 1 м. 2 п., высота карниза – 1м. 10 п.
§ Выступ карниза равен 1 м. 14 п.
Правило несвешиваемости
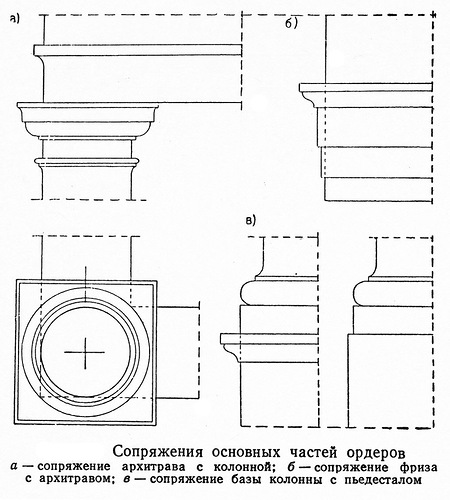
При использовании ордеров в проектировании необходимо строго следить за правильностью сопряжений их частей: базы колонны с пьедесталом, колонны архитравом и архитрава с фризом.
Существенное значение при этих сопряжениях имеетправило несвешиваемости, заключающееся в том, что отвесы выступающих опорных частей не должны внизу встречать пустоту. В приведенных сопряжениях выполнение этого правила обеспечивается тем, что выше- и нижележащие опорные элементы лежат в одной вертикальной плоскости.
В некоторых случаях нижележащий опорный элемент может выступать против верхнего, но не наоборот. Так, например, делается сопряжение пьедестала с базой колонны в том случае, когда пьедестал не имеет карниза.
Благодаря правилу несвешиваемости обеспечивается равновесие и устойчивость ордерных форм, как конструктивной системы.
Дата добавления: 2019-01-14; просмотров: 121; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!