Пример 5. Решить заданное дифференциальное уравнение
Практическое занятие №1
Тема: Математическое описание систем с помощью дифференциальных уравнений. Методы решения дифференциальных уравнений.
Цель: Получение практических навыков описания систем с помощью дифференциальных уравнений
Исходные теоретические сведения
Подобие описания систем различной природы. Мир технических систем разнообразен. Однако математика и физика выявили простые параллели в этом сложном мире. Можно выделить ряд энергетических доменов, которым принадлежат те или другие системы или их модули. Это электрический, магнитный, термальный, гидравлический, акустический, механический и ротационный домены. Так же существуют два фундаментальных постулата. Первый постулат гласит, что материя не может появиться ни откуда и не может исчезнуть в никуда. Второй постулат утверждает то же самое в отношении энергетического потенциала. Эти постулаты имеют частные формулировки для каждого энергетического домена. Например, для электрического домена это первый и второй законы Кирхгофа. Каждый из энергетических доменов характеризуется двумя физическими величинами первого и второго рода. В случае электрического домена - это электрические ток и напряжение соответственно. Эти парные физические величины, в каждом энергетическом домене, связаны между собой законом Ома в соответствующей формулировке (существуют: электрическое, магнитное, термальное, гидравлическое, акустическое, механическое и ротационное сопротивления). Так же следует отметить, что произведение физических величин первого и второго рода всегда есть мощность.
|
|
|
Представленная система параллелей позволяет понять, что математическое описание процессов движения координат систем принадлежащих разным энергетическим доменам подобно, и может быть предметом изучения одной науки, которая называется "Теория систем автоматического регулирования". Более того, в последние годы, приобретен успешный опыт применения методов этой теории при решении задач управления в экономических, финансовых и других нетехнических системах.
Способы описания систем. Современная теория автоматического управления оперирует преимущественно с моделями динамических систем. При этом рассматриваются в общем случае многомерные системы, т.е. системы произвольного порядка со многими входами и многими выходами, в связи, с чем широко используются векторно-матричные уравнения и аппарат векторной алгебры. Для получения модели исследуемая динамическая система представляется в виде “черного ящика” с некоторым числом входных и выходных каналов (рис. 1, а).
|
|
|
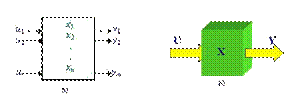
Рис.1. Скалярное (а) и векторное (б) представления динамической системы в виде "черного ящика"
Все переменные, характеризующие систему, можно разделить на три группы.
1. Входные переменные или входные воздействия, генерируемые системами, внешними по отношению к исследуемой системе. Входные переменные – это модели внешних сигналов, подразделяемых обычно на две группы:
– воздействия среды, в которой находится система;
– управляющие сигналы.
Переменные первой группы – это возмущения среды, вызванные внешними по отношению к системе управления причинами. Примерами таких возмущений могут быть порывы ветра – для летящего самолета, течение воды – для плывущего корабля, изменение поля тяготения вблизи больших масс небесных тел – для космического корабля и т.д. Если закон изменения такого возмущения известен (например, изменение давления воздуха с высотой полета самолета), то это возмущение можно учесть в виде переменной второй группы.
Переменные второй группы – это так называемые, контролируемые возмущения. Их можно разделить на учтенные возмущения внешней среды и управляющие воздействия. Последние из них являются результатом сравнения выходной информации системы с заданием и выработки управляющего сигнала на коррекцию поведения системы на основе результатов сравнения .
|
|
|
Входные переменные характеризуются вектором входа.
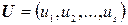 ,
,
где s − число входов.
2. Выходные переменные, характеризующие реакцию системы на входные воздействия и возмущения внешней среды. Представляются вектором выхода
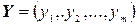 ,
,
где m − число выходов.
3. Промежуточные (внутренние) переменные, характеризующие внутреннее состояние системы, − переменные состояния, представляются вектором
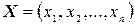 ,
,
где n − число переменных состояния.
Совокупность входов можно рассматривать как один обобщенный вход, на который воздействует вектор входа U, совокупность выходов как вектор Y, а совокупность промежуточных координат, характеризующих состояние системы, – как вектор состояния X (см. рис. 1.26, б).
Собственно система, ее входы и выходы − это три взаимосвязанных объекта, которые в каждой конкретной ситуации определяются соответственно математической моделью системы, заданием множеств входных и выходных переменных.
В качестве математических средств описания и исследования систем управления используются:
− дифференциальные уравнения;
|
|
|
− преобразование Лапласа;
− преобразование Фурье.
Описание многомерных систем обычно достаточно сложно и связано с большим объемом вычислений, поэтому при дальнейшем рассмотрении систем управления мы ограничимся элементами, а затем и системами с одним входом и одним выходом. При этом в качестве элементов систем будем рассматривать электрические схемы. Правомерность такого подхода определяется следующими соображениями:
1. Из всех возможных видов систем они для нас наиболее известны.
2. Протекающие в них процессы зависят от одной, наиболее существенной для нас переменной – времени.
3. Уравнения протекающих в них процессов можно линеаризовать.
Поскольку задача математического описания системы состоит в определения соотношения «вход-выход», то мы и рассмотрим ее решение для простейших электрических схем, которые будем рассматривать как элементы для построения систем.
Простейшие элементы линейных систем управления (с одним входом и одним выходом) могут быть описаны одним дифференциальным уравнением с постоянными коэффициентами. Составив и решив дифференциальное уравнение, описывающее систему, можно определить характер изменения входного сигнала и его значение в любой момент времени.
Обыкновенное линейное дифференциальное уравнение n -го порядка с постоянными коэффициентами обычно записывается так:
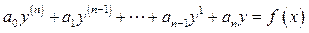 (1)
(1)
Обычно оно дополняется начальными условиями: f(0), f ¢(0),…, f(n-1) (0).
Если 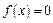 , то уравнение называется однородным.
, то уравнение называется однородным.
Полным решением (1) называется сумма общего решения соответствующего ему однородного линейного уравнения и любого частного решения неоднородного линейного дифференциального уравнения.
Общее решение однородного линейного дифференциального уравнения n-го порядка представляется функцией
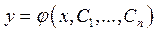 ,
,
зависящей от n произвольных постоянных 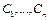 и обращающей уравнение (1) в тождество при любых значениях этих постоянных.
и обращающей уравнение (1) в тождество при любых значениях этих постоянных.
Получение общего решения однородного линейного дифференциального уравнения n-го порядка классическим методом производится следующим образом.
При замене 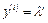 из однородного уравнения получаем характеристическое уравнение дифференциального уравнения (1)
из однородного уравнения получаем характеристическое уравнение дифференциального уравнения (1)
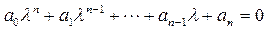 . (2)
. (2)
Если λ1, λ2,…, λn – корни характеристического уравнения (2), то любая функция 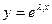 является решением дифференциального уравнения (1). Общее решение однородного линейного дифференциального уравнения n-го порядка представляет собой сумму следующих функций:
является решением дифференциального уравнения (1). Общее решение однородного линейного дифференциального уравнения n-го порядка представляет собой сумму следующих функций:
– 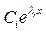 , где λ i – простой действительный корень уравнения (2);
, где λ i – простой действительный корень уравнения (2);
– 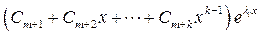 , где λ i – k-кратный действительный корень уравнения (2);
, где λ i – k-кратный действительный корень уравнения (2);
– 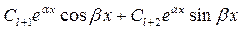 для каждой пары простых комплексно сопряженных корней уравнения (2);
для каждой пары простых комплексно сопряженных корней уравнения (2);
– 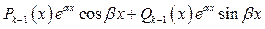 для каждой пары k-кратных комплексно сопряженных корней уравнения (2);
для каждой пары k-кратных комплексно сопряженных корней уравнения (2);
Частным решением неоднородного линейного дифференциального уравнения n-го порядка называется любая конкретная функция, являющаяся решением этого уравнения.
Существуют различные методы решения неоднородных линейных дифференциальных уравнений n-го порядка, зависящие от вида правой части уравнения (1), т.е. от 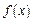 . Наиболее общим методом решения является метод вариации постоянных, состоящий в следующем.
. Наиболее общим методом решения является метод вариации постоянных, состоящий в следующем.
Пусть
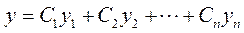
есть общее решение однородного уравнения, представляющего собой уравнение (1) с правой нулевой частью. Тогда решение неоднородного уравнения (1) ищется в виде
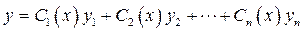 ,
,
где функции 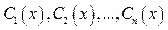 определяются из системы
определяются из системы
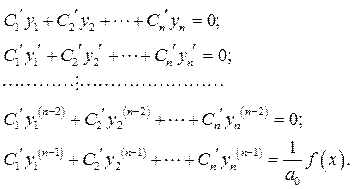 (3)
(3)
Работа в аудитории
2.1.Анализ примеров
Пример 1.Составить уравнение электрической системы, представленной на рис.1.
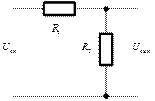
Рис. 1
Решение. На основании законов Ома и Кирхгофа имеем:
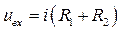 ;
;
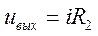 .
.
Тогда, выразив 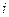 и подставив из одного уравнения в другое, получим:
и подставив из одного уравнения в другое, получим:
 .
.
или окончательно
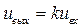 , где
, где 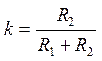 .
.
Ответ: 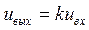 , где
, где 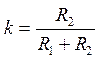 .
.
Пример 2. Составить дифференциальное уравнение электрической системы, представленной на рис.2.
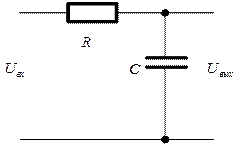
Рис. 2
Решение. На основании законов Ома и Кирхгофа имеем:
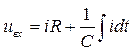 ;
;
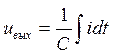 ;
;
Тогда имеем:
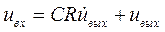
Обозначив 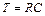 , окончательно получим:
, окончательно получим:
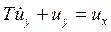 .
.
Ответ: 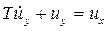 , где
, где 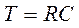 .
.
Пример 3. Составить дифференциальное уравнение электрической системы, представленной на рис.3.
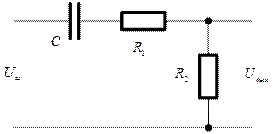
Рис. 3
Решение. На основании законов Ома и Кирхгофа имеем:
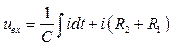 ; (1)
; (1)
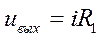 ; (2)
; (2)
Тогда, продифференцировав второе уравнение, имеем:
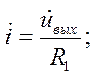
Продифференцировав первое уравнение и подставив, второе в первое получим:
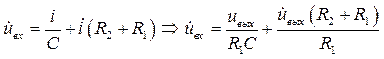 .
.
Окончательно, получим:
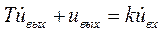 ,
,
где 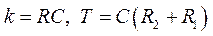 .
.
Ответ: 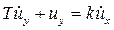 , где
, где 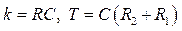 .
.
Пример 4. Решить дифференциальное уравнение
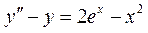 . (4)
. (4)
Решение. Составляем характеристическое уравнение и находим его корни.
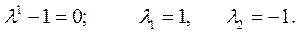
Общее решение однородного уравнения
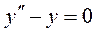
имеет вид
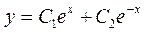 ,
,
где 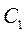 и
и 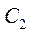 – некоторые произвольные постоянные.
– некоторые произвольные постоянные.
Полное решение уравнения (3) будем искать в виде
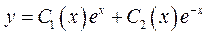 . (5)
. (5)
Для этого необходимо решить систему алгебраических уравнений вида (3)
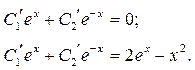
Решая ее, получим
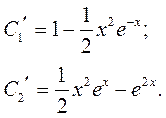
Теперь можно определить функции 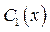 и
и 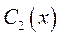 , интегрируя полученные выражения
, интегрируя полученные выражения
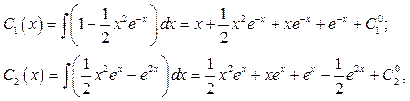
где 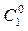 и
и 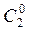 - постоянные интегрирования.
- постоянные интегрирования.
Подставляя найденные 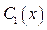 и
и 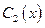 в (5), получим полное решение уравнения (1) в форме (5)
в (5), получим полное решение уравнения (1) в форме (5)
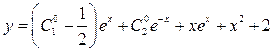 ,
,
Обозначив 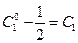 и
и 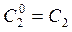 , окончательно получим
, окончательно получим
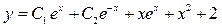 .
.
Пример 5. Решить заданное дифференциальное уравнение
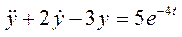
при 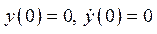 классическим методом и построить график его решения.
классическим методом и построить график его решения.
Решение.
1) Найдем общее решение однородного дифференциального уравнения.
Составляем характеристическое уравнение:
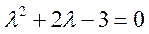
Найдем корни данного квадратного уравнения:
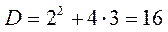 ,
,
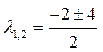 ,
, 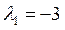 ,
, 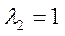 .
.
Таким образом, общее решение представим в виде:
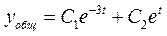 ,
,
где 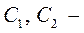 неизвестные константы, определяемые на основании начальных условий.
неизвестные константы, определяемые на основании начальных условий.
2) Найдем частное решение дифференциального уравнения.
Частное решение будем искать в виде:
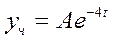 .
.
Возьмем первую и вторую производные от частного решения:
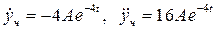 .
.
Подставим производные и само выражение частного решения в исходное дифференциальное уравнение, получим:
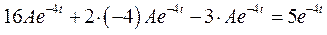 .
.
Приведем подобные и произведем необходимые сокращения:
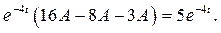
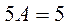 , или
, или 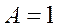 .
.
Таким образом, частное решение представим в виде:
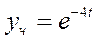 .
.
3). Найдем полное решение дифференциального уравнения.
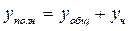 .
.
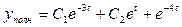 .
.
С учетом начальных условий получим:
 .
.
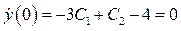 .
.
Найдем 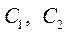 :
:
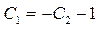 ,
,
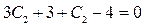 .
.
Отсюда получаем:
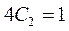 , т.е.
, т.е. 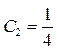 и, следовательно,
и, следовательно, 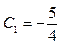
Таким образом, полное решение уравнения имеет вид:
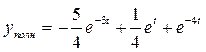 .
.
4). Для построения графика найдем точки его начала и конца.
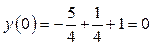 .
.
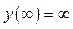 .
.
Найдем несколько промежуточных точек и выстроим график:
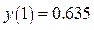 ,
, 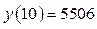 , и т.д.
, и т.д.
График решения представлено на рис. 4.
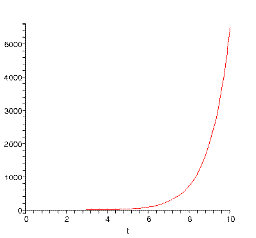
Рис. 4.
Дата добавления: 2019-01-14; просмотров: 217; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
