Отсечение. Алгоритм Кируса Бека отсечения отрезка.

Алгоритм

1. D=P2-P1
2. tн=0, tв=1
3. Цикл по всем граням i=1:N
1. Вычисление nвнi
2. Di=D*nвнi
3. Wi=(P1-fi)*nвнi
4. Di=0?
1. да. Wi≥0? нет - Конец. да - продолжаем
2. нет. t=-Wi/Di; Di>0?
1. да. t>1?
1. нет. tн=max(tн, t)
2. да. Конец
2. нет. t<0?
1. нет. tв=min(tв, t)
2. да. Конец
4. tн≤tв? да – нарисовать(P(tн), P(tв))
5. Конец

Внутреннее и внешнее отсечение. Определение выпуклости многоугольника; определение нормали; разбиение невыпуклых многоугольников. Триангуляция многоугольников.

 

Внутреннее отсечение – определяем части отрезка внутри отсекателя и вычерчиваем.

Внешнее отсечение – определяем части вне отсекателя и вычерчиваем.

Определение выпуклости

• Вычислить векторные произведения всех пар смежных сторон.

1. Если все = 0 – многоугольник вырожден в отрезок.
2. Все разных знаков – многоугольник невыпуклый.
3. Все ≥0 – выпуклый, нормали ориентированы влево от рёбер.
4. Все ≤0 – выпуклый, нормали вправо.

• Разбиение

1. Перенести в (0, 0) i-ую вершину
2. Повернуть вокруг (0, 0), чтобы i+1-ая вершина оказалось на +части оси x
3. Вычислить знаки ординат всех i+2-ых вершин
1. =0 – вырожден в отрезок
2. одинаковы – выпуклый относительно этого ребра
3. разные – невыпуклый, разрезаем на 2 части вдоль оси. далее работаем с двумя многоугольниками

Определение внутренней нормали

Отсечение многоугольников. Алгоритм Сазерленда Ходжмена.

 

Возможные варианты взаимного расположения.

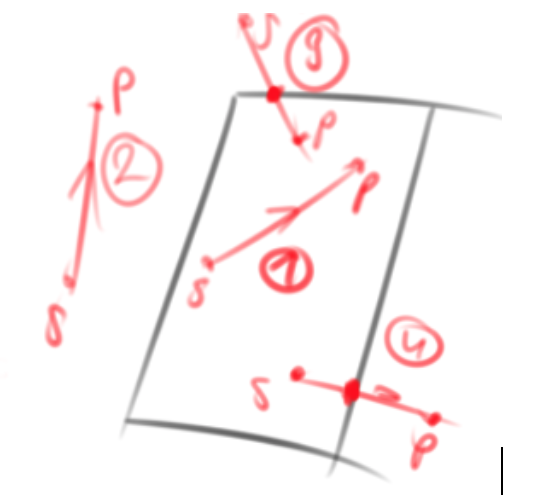
1. обе вершины отрезка SP видимы, отрезок целиком видим. В результат заносятся точки S и P
2. Обе вершины невидимы, отрезок целиком невидим. В результат заносится 0 точек
3. S невидима, P видима, отрезок частично видим. В результат заносится точка пересечения (надо найти) и P.
4. Наоборот. S и точка пересечения.

Алгоритм

1. определить видимость точки (вершины рёбер)
   а) использовать скалярное произведение PjAi(вектор из вершины в точки) * n(внутр нормаль), >=0 точка видима, <0 невидима(как в Кирусе-Беке)

б) использовать пробную функцию (на основе уравнения прямой/совпадающей с ребром многоугольника) F =ax + by + c знак функции для исследуемой функции надо сравнить со знаком пробной функции точки, положение которой известно

в) использование векторного произведения AiPj(из вершины в точку) * AiAi+1(вектор совпадающ с ребром), >=0 точка Pj видима(есди равно точка на границе и она видима) контур обходится по часовой стрелке

1. находить точки пересечения(убедиться в ее наличии)
   искать точку пересечения ребра многоугольника с прямой == стороной отсекателя(когда видимость концов ребра различная)

В данном алгоритме рассматривается конкретный вариант нахождения: ищется точка пересечения прямой, проходящей через ребро отсекателя, с ребром отсекаемого многоугольника. Поскольку отрезки имеют произвольное расположение, удобно использовать параметрическую форму записи: P(t) = P1 + (P2-P1)t, где 0<=t<=1 – ребро многоугольника, и Q(s) = Q1 + (Q2-Q1)s – ребро отсекателя.(прямая s без ограничений) P(t)=Q(s): Предварительно нужно убедиться в непараллельности прямых – точка пересечения должна существовать. Это определяется с помощью видимости концов ребра многоугольника – если видимость разная, то точка пересечения есть. Начальная вершина очередного ребра является одновременно и конечной вершиной для предыдущего ребра. Эта вершина анализируется (и заносится в результат если видима) на предыдущем шаге.

Данный алгоритм имеет недостаток – можно столкнуться с ситуацией построения «ложных ребер» (I2I3).

Мы работаем с массивом вершин, вершины обходятся последовательно – ложным будет ребро, которое обходится два раза.

Алгоритм

def sutherland_hodgman(clip, pol, norm):

# дублируем начальную вершину отсекателя в конец

clip.append(clip[0])

 

s = None

f = None

# цикл по вершинам отсекателя

for i in range(len(clip) - 1):

   new = [] # новый массив вершин

   for j in range(len(pol)): # цикл по вершинам многоугольника

       if j == 0:

           f = pol[j]

       else:

           t = is_intersection([s, pol[j]], [clip[i], clip[i + 1]], norm)

           if t:

               new.append(t)

 

       s = pol[j]

       if is_visiable(s, clip[i], clip[i + 1], norm):

               new.append(s)

 

   if len(new) != 0:

       t = is_intersection([s, f], [clip[i], clip[i + 1]], norm)

       if t:

           new.append(t)

 

   pol = copy.deepcopy(new)

 

if len(pol) == 0:

   return False

else:

   return QPolygonF(pol)

---

Дата добавления: 2019-01-14; просмотров: 758; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!