Приведение к каноническому виду линии 2-го порядка
Рассмотрим вначале частный случай линии 2-го порядка, при В = 0, то есть от-сутствует произведение 
:
В этом случае преобразование к каноническому виду сводится к выделению полных квадратов по х и y и переносу в правую часть свободного члена. Разделив обе части полученного уравнения на свободный член, получим каноническое уравнение соответствующей кривой.
В общем случае для приведения к каноническому виду нужно для матрицы, соответствующей 
, т. е. 
, найти собственные значения и собственные векторы, которые и определят новую систему координат, в которой кривая имеет канонический вид.
Этот алгоритм будет рассмотрен подробно на примере.
Классификация линий 2-го порядка. Окружность
Окружность – геометрическое место точек, равноудаленных от одной точки, называемой центром.
Пусть 
, тогда каноническое уравнение окружности имеет вид (рис. 4)
, где R – радиус окружности.
Если центр совпадает с началом координат, уравнение принимает вид: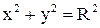 
(рис.5).
Y Y
y0 R
C R
x0 x O x
|
|
|
Рис. 4 Рис. 5
Эллипс
Эллипс – геометрическое место точек, для которых сумма расстояний от двух фиксированных точек плоскости, называемых фокусами, есть величина постоянная.
Если центр эллипса совпадает с началом координат, то каноническое уравнение имеет вид 
.
Если a > b, то эллипс вытянут вдоль оси ОХ, фокусы расположены также на ОХ симметрично относительно начала координат, а фокусное расстояние и эксцентриситет определяются по формулам: 
(рис. 6).
Если b > a, то эллипс вытянут вдоль оси OY, фокусы располагаются на оси OY, симметрично относительно начала координат, а фокусное расстояние и эксцентриситет определяются по следующей формуле: 
(рис. 7).
Y Y
F2
|
|
|
b
b a
F1 O F2 x O x
F1
Рис. 6 Рис. 7
Гипербола
Гипербола – геометрическое место точек, для которых разность расстояний от двух фиксированных точек плоскости, называемых фокусами, есть величина постоянная.
Если центр гиперболы совпадает с началом координат, то ее уравнение имеет канонический вид:
.
Это уравнение распадается на два уравнения гипербол, которые называются сопряженными: 
(рис. 8) и 
(рис. 9).
Y
Y
F2
|
|
|
B
F1 A b B F2
a O x O x
A
F1
Рис. 8 Рис. 9
Точки A и B (рис. 8) – вершины гиперболы. Диагонали основного прямоугольника, являющиеся асимптотами гиперболы имеют уравнения: 
. Уравнения директрис: 
Уравнения асимптот гиперболы (рис. 9): 
. Уравнения директрис: 
.
Парабола
Парабола – геометрическое место точек, для каждой из которых расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой прямой, называемой директрисой.
Парабола не является центральной кривой; она имеет одну ось симметрии, с которой она пересекается в единственной точке, называемой ее вершиной.
|
|
|
Если координатная система выбрана так, что вершина находится в начале координат, то канонические уравнения параболы будут иметь вид 
(рис. 10) и 
(рис. 11), где 
.
Y
O x
Рис. 10
| Y
O x
Рис. 11
|
Осью симметрии парабол (рис. 10) является ось ОХ, уравнения директрис имеют вид: 
и 
.
Осью симметрии парабол (рис. 11) является ось OY, уравнения директрис имеют вид: 
и 
.
Задача 2. Составить уравнение гиперболы, фокусы которой расположены на оси абсцисс симметрично относительно начала координат, зная, что 2с=6, 
.
Решение. Каноническое уравнение такой гиперболы имеет вид
.
Из условия 
. Составим систему
. Из системы находим 
; 
.
Каноническое уравнение будет иметь вид 
.
Ответ: Каноническое уравнение гиперболы .
Задача 3. Определить точки пересечения прямой 
и параболы 
.
Решение. Выразим y в уравнении прямой через х и подставим в уравнение параболы:
,
.
По теореме Виета 
, откуда 
Находим ординаты
Точки пересечения имеют координаты 
.
Ответ: Точки пересечения прямой и параболы 
.
Задача 4. Установить, является ли линия 2-го порядка 
центральной и найти координаты ее центра.
Решение. Вычислим определитель матрицы квадратичной формы:
Так как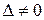 
, линия является центральной. Найдем координаты центра 
.
,
.
Ответ: Кривая второго порядка является центральной, центр С(3, -2).
Задача 5. Установить, приведением к каноническому виду какую кривую 2-го порядка определяет следующее уравнение: 
. Найти координаты центра (вершины), полуоси, эксцентриситет.
Решение. Выделим полные квадраты по х и у, так как член ху отсутствует в уравнении:
,
.
Делим обе части на свободный член:
.
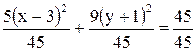Получим каноническое уравнение эллипса:
Центр С(3,-1), полуоси 
.
Ответ: Кривая центральная С(3,-1), 
.
Задача 6. Следующее уравнение привести к каноническому виду, определить его тип, изобразить на чертеже оси первоначальной и новой системы координат и построить кривую, соответствующую этому уравнению:
.
. Откуда следует, что кривая не является центральной.
Найдем собственные значения этой матрицы:
,
,
.
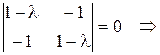
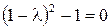Найдем собственные векторы, соответствующие найденным собственным значениям.
1. 
.
2. 
Проверим 
что означает: ориентация правильная, совпадает с исходным базисом.
Нормируем векторы и вычислим базисные векторы новой системы координат:
Уравнение в новом базисе имеет вид
.
Системы координат ХОУ с базисом 
и 
с базисом 
связаны формулами
Подставляя в исходное уравнение вместо х и у их выражения, получим
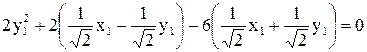
или
.
Выделяя полный квадрат по у, получим
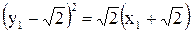
Эта парабола симметрична относительно оси 
(рис.12), О1 – вершина, находящаяся в точке 
. В новой системе 
координат уравнение примет вид
.
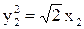Y
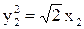
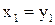
O1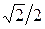 
О Х
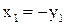
Рис. 12
КОНТРОЛЬНЫЕ ЗАДАНИЯ
Задача 1
Даны координаты точек А,В,С. Найти:
a) уравнение стороны АС треугольника АВС;
b) уравнения медиан СС1 и АА1 D АВС;
c) точку пересечения медиан СС1 и АА1 ;
d) угол А в D АВС;
| 1. А(-1;0) В(0;4) С(4;2) | 2. А(-2;0) В(0;3) С(3;-1) |
| 3. А(0;4) В(4;2) С(-1;0) | 4. А(2;3) В(-5;-4) С(6;1) |
ЗАДАЧА 2
Составить уравнение окружности в каждом из следующих случаев.
a) Центр окружности находится в точке С(2;-3), R=7.
b) Окружность проходит через начало координат, центр окружности находится в точке С(6,8).
Найти точки пересечения прямой и эллипса.
с) 
д) 
Определить полуоси a и b, эксцентриситет, асимптоты следующих гипербол:
a)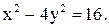 
b) 
Определить точки пересечения эллипса и параболы:
Дата добавления: 2019-01-14; просмотров: 542; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!