Расчет параметров модели управления запасами с фиксированным размером заказа

Тема 4. Основные модели управления запасами

Вопрос 1. Модель управления запасами с фиксированным размером заказа.

Вопрос 2. Модель управления запасами с фиксированным интервалом времени между заказами.

Вопрос 3. Модели управления запасами в условиях изменяющейся потребности.

 

Изменение объема запаса во времени — основная проблема обеспечения потребности в запасе данного места хранения. Не­обходимо содержать запас в таком объеме, чтобы, невзирая на особенности реализации пополнения и потребления запаса, он всегда был достаточен для обслуживания потребления на задан­ном уровне. Не имея возможности напрямую влиять на характерис­тики потребности в запасе, специалисты по управлению запасами используют возможности влиять на характеристики поставки. При этом главными вопросами являются объем заказа и момент, когда следует заказать товарно-материальные ценности для вос­полнения запаса.

Таким образом, теоретически имеется две модели управления запасами:

1) модель управления запасами с фиксированным размером за­каза (или двухбункерная система ( two - bin system ));

2) модель управления запасами с фиксированным интервалом времени между заказами.

Эти модели являются основными в управлении запасами. Все огромное разнообразие алгоритмов управления запасами основы­вается на методике фиксированного размера заказа или методике фиксированного интервала времени между заказами.

 

Вопрос 1. Модель управления запасами с фиксированным размером заказа

 

Методика управления запасами на основе фиксации размера заказа заключается в том, что заказы на пополнение запаса дела­ются в момент снижения запаса до заранее определенного, поро­гового уровня запаса в объеме, равном оптимальному размеру за­каза (рис. 4.1). Все параметры модели рассчитываются таким об­разом, что при соблюдении исходных данных модель гарантирует бездефицитное обслуживание потребности в условиях определен­ности (т.е. в условиях постоянного темпа потребления).

Исходные данные для расчета параметров модели с фиксирован­ным размером заказа:

1) объем потребности в запасе, единиц;

2) оптимальный размер заказа, единиц;

3) время выполнения заказа, дни;

4) возможная задержка поставки, дни.

Расчетные параметры модели с фиксированным размером за­каза (см. рис. 4.1):

1) максимальный желательный запас, единиц;

2) пороговый уровень запаса, единиц;

3) страховой запас, единиц.

Максимальный желательный запас в отличие от последующих двух основных параметров не имеет непосредственного воздей­ствия на движение запаса в целом. Этот уровень запаса определя­ется для отслеживания целесообразной загрузки площадей склада с точки зрения критерия минимизации совокупных затрат.

Пороговый уровень запаса (или точка повторного заказа, reorder point ) определяет уровень запаса, при достижении которого произ­водится очередной заказ. Величина порогового уровня должна быть рассчитана таким образом, что поступление заказа на склад происходит в момент снижения текущего запаса до уровня страхового запаса. При расчете порогового уровня задержка поставки не учитывается.

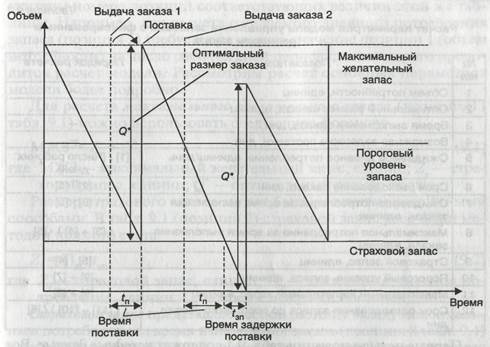
Рис. 4.1. Иллюстрация движения запаса при фиксированном размере заказа

 

Страховой (или гарантийный) запас позволяет удовлетворять потребность в запасе на время предполагаемой задержки поставки. При этом под возможной задержкой поставки подразумевается максимальная возможная задержка. Восполнение страхового за­паса производится во время последующих поставок путем создания порогового уровня запаса.

Расчет параметров модели управления запасами с фиксирован­ным размером заказа приведен в табл. 4.1. Все параметры модели управления запасами с фиксированным размером заказа рассчитаны в табл. 4.1 (см. также рис. 4.1) таким образом, что при соблюдении заданных границ исходных данных за время выполнения заказа запас снижается с порогового до стра­хового уровня запаса. При получении поставки в срок фиксиро­ванный размер заказа восполняет запас до желательного макси­мального уровня. При наличии сбоев поставок бездефицитность обслуживания потребления обеспечивает страховой запас.

Таблица 4.1

Расчет параметров модели управления запасами с фиксированным размером заказа

№ п/п	Показатель	Порядок расчета
1	Объем потребности, единиц	—
2	Оптимальный размер заказа, единиц	—
3	Время выполнения заказа, дни	—
4	Возможная задержка поставки, дни	—
5	Ожидаемое дневное потребление, единиц/день	[1]/[Число рабочих дней]
6	Срок расходования заказа, дни	[2] / [5]
7	Ожидаемое потребление за время выполнения заказа, единиц	[3] • [5]
8	Максимальное потребление за время выполнения заказа, единиц	([3] + [4]) • [5]
9	Страховой запас, единиц	[5] • [4]
10	Пороговый уровень запаса, единиц	[9] + [7]
11	Максимальный желательный запас, единиц	[9] + [2]
12	Срок расходования запаса до порогового уровня, дни	([11 ] - [10]) / [5]

 

Первые четыре позиции табл. 4.1 содержат исходные данные. Все позиции, включая позиции 3 и 4, предполагаются неизменными. Например, если происходит задержка поставки, то время этой за­держки строго равно значению, которое задается в позиции 4 таб­лицы.

Объем потребности в запасе определяется по плановым или про­гнозным оценкам, которые могут быть получены на основе плановых показателей или рассчитанного прогноза.

Оптимальный размер заказа определяется по модели оптимального размера заказа Вильсона и ее модификаций.

Время выполнения заказа включает длительность периода от мо­мента принятия решения о восполнении запаса до момента опри­ходования поступившего заказа на склад. Структура этого периода рассмотрена в теме 2 вопрос 1.

Время задержки поставки представляет собой оценку возмож­ного отклонения от заданного времени выполнения заказа, прово­димую, как правило, на основе анализа статистики выполнения заказов прошлых периодов.

Расчет параметров модели управления запасами с фиксирован­ным размером заказа в табл. 4.1 представлен в виде, удобном для проведения расчетов в Microsoft Excel : в записи формулы расчета указаны номера позиций соответствующих величин этой же таб­лицы. Например, для расчета ожидаемого дневного потребления запаса (позиция 5) требуется разделить значение позиции 1 (объем потребности) на число рабочих дней периода, для которого прово­дится расчет модели. Рассмотрим расчет основных параметров модели более подробно.

Для расчета максимального желательного запаса (позиция 11 табл. 4.1) можно использовать следующую формулу:

,                         (4.1)

где  — максимальный желательный запас, единиц;  — стра­ховой запас, единиц;  — оптимальный размер заказа. Размер страхового запаса может быть рассчитан различными способами. В табл. 4.1 (позиция 9) страховой запас рассчитан ме­тодом прямого счета:

                      (4.2)

где  — страховой запас, единиц;  — ожидаемое дневное по­требление, единиц;
 — время задержки поставки, дни.

Страховой запас представляет собой разницу между максималь­ным потребление за время выполнения заказа (позиция 8 табл. 4.1) и ожидаемым потреблением за время выполнения заказа (позиция 7 табл. 4.1) (см. также рис. 4.1):

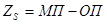                           (4.3)

где  — страховой запас, единиц;  — максимальное потребле­ние за время выполнения заказа, единиц;  — ожидаемое потребление за время выполнения заказа, единиц. В свою очередь, максимальное потребление за время выполне­ния заказа (позиция 8 табл. 4.1) рассчитывается по формуле

                     (4.4)

где  — максимальное потребление за время выполнения зака­за, единиц;
 — ожидаемое дневное потребление, единиц;  — время выполнения заказа, дни;
 — время задержки по­ставки, дни.

Ожидаемое дневное потребление  рассчитывается исходя из ожидаемой потребности в запасе за весь период (см. позицию 5 табл. 4.1):

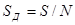                       (4.5)

где 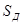 — ожидаемое дневное потребление, единиц; — объем по­требности в запасе, единиц; — число рабочих дней в плано­вом периоде.

Ожидаемое потребление за время выполнения заказа  (см. позицию 7 табл. 4.1) рассчитывается как произведение ожидаемо­го дневного потребления на время выполнения заказа:

                      (4.6)

где  — ожидаемое потребление за время выполнения заказа, единиц;
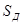 — ожидаемое дневное потребление, единиц;  — время выполнения заказа, дни.

Страховой запас  может быть также рассчитан и по другим формулам, имеющим статистический, вероятностный или эмпи­рический характер (см. формулы темы 1).

Максимальный желательный запас в модели управления запа­сами с фиксированным размером заказа является экономически целесообразным, ориентированным на учет совокупности значи­мых факторов формулы Вильсона. Максимальный же­лательный запас является важным фактором планирования ис­пользования складских площадей и определения объема склада. В рассматриваемой модели формула Вильсона является инстру­ментом интеграции сфер управления запасами и управления скла­дированием и грузопереработкой.

Пороговый уровень запаса рассчитывается следующим образом (см. позицию 10 табл. 4.1):

                                        (4.7)

где  — пороговый уровень запаса, единиц;  — страховой за­пас, единиц; 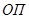 — ожидаемое потребление за время выпол­нения заказа.

Срок расходования запаса до порогового уровня (см. пози­цию 12 табл. 4.1) имеет справочное значение.

       Следует подчеркнуть, что параметры этой модели также рассчитываются в условиях колебании потребности в запасе и задержках поставок, что будет рассмотрено на практическом занятии.

Классическая модель управления запасами с фиксированным размером заказа работает автоматически, т.е. без привлечения спе­циалистов для принятия решений о восполнении запаса, с гаран­тией отсутствия дефицита запаса только в случае постоянного потребления запаса.

Анализ классической модели управления запасами с фиксированным размером заказа показывает, что в условиях колебания потребности, так же как и при колебании времени выполнения заказа и времени задержки поставки, для обеспечения отсутствия дефицита запаса требуется доработать классический алгоритм фик­сированного размера заказа.

---

Дата добавления: 2019-01-14; просмотров: 4072; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!