Моделирование процессов в исследуемой системе.

1. Построить динамическую модель системы с использованием пакета MATLAB.

2. Установить малые значения коэффициентов k_1,k₂ = 0.05, запустить модель и убедиться в устойчивости системы.

3. Определить экспериментально область устойчивости на плоскости коэффициентов k_1,k₂ , для чего:

• установив фиксированные значения k₂ , увеличивать коэффициенты k₁ до величины k_1кр , соответствующей возникновению незатухающих колебаний в САУ. Повторяя эту операцию для ряда значений k ₂ , получить экспериментальную границу k_1кр = j( k₂)

• фиксируя k₁ и увеличивая k₂ до величины k_2кр , соответствующей возникновению незатухающих колебаний в САУ, построить границу устойчивости k_2кр = j(k₁). Провести сравнение теоретической и экспериментальной областей.

5. Рассмотреть и зарисовать переходные процессы входной сигнал при значениях параметров:

• соответствующих расчетной части

• находящихся вблизи границы устойчивости.

6. Установив соответствующие значения коэффициентов, рассмотреть и зарисовать процесс конечной деятельности при нулевых начальных условиях

VI. ОФОРМЛЕНИЕ ОТЧЕТА

В отчете должна быть представлены структурная схема системы, процесс вывода передаточных функций и их выражения, теоретическая и экспериментальная области устойчивости на плоскости k_1,k₂ коэффициенты
k₁⁰_,k₂⁰,соответствующие процессам конечной длительности, теоретический и экспериментальный процессы конечной длительности, схема моделирования системы в среде SIMULINK.

VII. КОНТРОЛЬНЫЕ ВОПРОСЫ

1.Что называется процессом конечной длительности?

2.В чем состоят условия существования процессов конечной длительности?

З. Как строится область устойчивости на плоскостях?

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Бесекерский В.А. Теория систем автоматического управления: [Учебное издание] / В.А. Бесекерский, Е.П. Попов .— 4-е изд., перераб. и доп. — СПб. : Профессия, 2004 .— 752с.

2. Горячев О.В. Основы теории компьютерного управления : учеб. пособие / О. В. Горячев, С. А. Руднев ; ТулГУ .— Тула : Изд-во ТулГУ, 2008 .— 220 с.

3. Мирошник И.В. Теория автоматического управления. Нелинейные и оптимальные системы: учебное пособие для вузов / И.В. Мирошник.— М.и др. : Питер, 2006 .— 272с. (23 экз.)

4. Пупков К.А. Методы классической и современной теории автоматического управления : учебник для вузов:в 5 т. Т.5. Методы современной теории автоматического управления / К.А. Пупков [и др.];под ред. К.А. Пупкова, Н.Д. Егупова .— 2-е изд., перераб. и доп. — М. : МГТУ им. Баумана, 2004 .— 784с.

ЛАБОРАТОРНАЯ РАБОТА № 3

АНАЛИЗ ЧАСТОТНЫХ СВОЙСТВ ДИСКРЕТНОЙ СИСТЕМЫ

I. ЦЕЛЬ И ЗАДАЧИ РАБОТЫ

Изучение особенностей частотного анализа дискретных систем; исследование особенностей прохождения высокочастотной гармонической помехи через линейную импульсную систему.

II . ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Функция , получаемая из Z-передаточной функции W(z) подстановкой 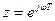, называется амплитудно-фазовой частотной характеристикой. Функция называется амплитудной частотной фазовой характеристикой, функция называется фазовой частотной характеристикой. Установившаяся реакция системы с передаточной функцией W(z) на дискретный гармонический сигнал 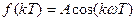определится выражением

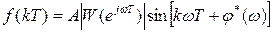, (1)

т.е. амплитуда выходного сигнала увеличивается в раз, а фаза изменяется на величину .

Рассмотрим прохождение непрерывного гармонического сигнала через дискретную систему, схема которой изображена на рис. 1. Так как импульсный элемент выделяет лишь дискретные значения входного сигнала, соответствующие моментам квантования, то в установившемся режиме при
t = kT , k =0,1,..., выходная величина по-прежнему будет определяться зависимостью (1). Однако может оказаться необходимым знать, что происходит в системе в любой момент времени, т.е. необходимо определить «полную» реакцию y ( t ),

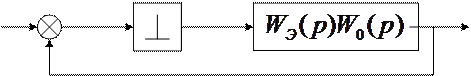f e e ^*

Рис. 1.

Частотные характеристики дискретной системы не позволяют определить эту реакцию. Для нахождения этой величины необходимы дополнительные сведения о частотных свойствах дискретной системы.

При прохождении через импульсный элемент спектр сигнала изменяется, в нем появляются дополнительные составляющие. Эта особенность оказывает существенное влияние на работу импульсной системы. Так при прохождении сигнала через идеальный импульсный элемент на его выходе будем иметь

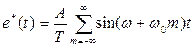, . (2)

Из формулы видно, что на выходе ИИЭ образуется бесконечное множество гармонических составляющих с частотами, отличающихся от исходных на w₀m, m = 0,±1,…. Дополнительные составляющие с частотами w_T= w ± w₀m, m = 1,2,... называются транспонированными составляющими. Таким образом, после ИИЭ сигнал содержит основную и транспонированную (перенесенные) составляющие. При этом наибольший интерес представляют два случая: преобразование низкочастотного сигнала в высокочастотную область ( w_T> w) и транспонирование высокочастотного сигнала в низкочастотную часть спектра ( w_T< w). В системах управления первый вариант возникает при воспроизведении низкочастотных полезных сигналов и в правильно спроектированной системе он не вызывает сложностей. При этом свойства объекта (непрерывной части) и частота квантования должны быть согласованы таким образом, чтобы непрерывная часть отфильтровывала высокочастотные транспонированные составляющие и на выходе, в основном, проявлялась бы основная, полезная составляющая.

Второй вариант транспонирования может привести к неприятному результату. Высокочастотный сигнал - это, как правило, помеха, которая не должна сказываться на работе системы. Однако, даже если непрерывная часть системы эффективно ослабляет самую высокую частоту w , то среди транспонированных частот, меньших основной, т.е. w - w₀, w - 2w₀,… могут оказаться частоты, попадающие в полосу пропускания непрерывной части. В этом случае на выходе могут возникнуть низкочастотные движения, являющиеся транспонированными составляющими высокочастотной помехи. Снижение величины таких транспонированных колебаний является важной задачей проектировщика. Обычно для этого используется предимпульсная фильтрация, т.е. фильтрация непрерывного сигнала до попадания его в ИЭ. Эффект такой фильтрации состоит в уменьшении амплитуды помехи, попадающей в ИЭ.

Пусть на вход замкнутой импульсной системы (рис.1) поступает гармонический сигнал

При этом в установившемся режиме в каждой точке замкнутого контура спектр сигнала состоит из основной с частотой w_т и транспонированных с частотами w ± w₀, w ± 2w₀,… составляющих. Рассмотрим задачу определения амплитуд отдельных составляющих сигнала на выходе непрерывной части y(t).

Рассмотрим вначале прямую цепь, связывающую сигналы e(t) и y(t). Предположим, что e(t) - гармонический сигнал частоты w_n , и найдем амплитуды отдельных составляющих сигнала y(t). Это достаточно просто. Действительно, известно, что если , то

т.е. на выходе ИИЭ возникает счетное множество составляющих, частоты которых известны, а амплитуды одинаковы. В силу линейности непрерывной части прохождение каждой составляющей через звено с передаточной функцией 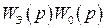может рассматриваться отдельно для каждой из частот w_T = w _n ± w ₀ m , m = 0,±1,…. Амплитуда соответствующей составляющей выходного сигнала определяется как

, (3)

где 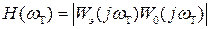- значение АЧХ непрерывной части для данной частоты w_T. Фазовые соотношения рассматривать не будем. Таким образом, если , то задача определения амплитуд А_у отдельных составляющих решена. Отметим, что величины не зависят от начальной фазы сигнала e(t).

В замкнутой системе сигнал e(t) не является гармоническим, он содержит множество составляющих с частотами w_T = w _n ± w ₀ m , m = 0,±1,…. Однако e(t) - входной сигнал ИИЭ - осуществляет из него выборку дискрет e(kT) , k =0,l,... и, в соответствии с частотными свойствами линейных импульсных систем, эти дискреты соответствуют гармонической решетчатой функции

Таким образом, реакция прямой цепи на реальный сигнал e(t) будет такой же, какой она была бы на гармонический сигнал (при этом, как уже было сказано, на оценку амплитуды начальная фаза не влияет). Амплитуда совпадает с амплитудой дискретной синусоиды (3) и она может быть определена с помощью АЧХ дискретной системы.

Окончательно можно предложить следующую процедуру определения амплитуд отдельных составляющих сигнала y(t) на выходе системы:

1. Найдем Z-передаточную функцию Ф(z), связывающую помеху с сигналом на входе ИИЭ

. (4)

2. Найдем соответствующую АФЧХ и выделим АЧХ А^*(w _n)

АФЧХ:

АЧХ : (5)

3. Найдем амплитуду дискретной синусоиды на входе ИИЭ

, (6)

где В - амплитуда, w _n - частота гармонического сигнала f(t).

4. Определим частоты транспонированных составляющих

w _T = w _n ± w₀m , m = 0,±1,…, (7)

5. Рассчитаем АЧХ непрерывной части системы на основной и транспонированных частотах.

. (8)

6. Определим амплитуды отдельных составляющих на входе системы

(9)

При выполнении 4-6 пунктов нужно задаться несколькими частотами, появление которых наиболее вероятно на выходе системы. Как правило, это наиболее низкие частоты, которые слабее отфильтровываются непрерывной частью.

III. ОБЪЕКТ ИССЛЕДОВАНИЯ, ПРИБОРЫ, ОБОРУДОВАНИЕ.

ОБЪЕКТ ИССЛЕДОВАНИЯ – система, структурная схема которой приведена на рис. 2.

В процессе работы система моделируется на персональном компьютере с использованием пакета MATLAB.

ПРИБОРЫ, ОБОРУДОВАНИЕ – персональный компьютер IBM PC.

IV. ЗАДАНИЕ НА РАБОТУ

Структурная схема исследуемой САУ представлена на рис.2.

f + e e e ^* ^y

- -

f ( t )

Рис. 2.

АИЭ осуществляет выборку и фиксацию на периоде квантования,

k =6, T = T₁= 1c , 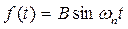, w _n = 3.3 × 6.28 1/ c , B = 10.

Требуется выявить частоты, для которых соответствующие составляющие на выходе системы будут иметь наибольшие в сравнении с прочими амплитуды (4-6 значений); рассчитать эти амплитуды; оценить влияние предимпульсной фильтрации на помехоустойчивость системы; провести экспериментальное исследование САУ.

V. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

Расчетная часть

1. При заданной преподавателем величине w _n по формуле (7) рассчитать спектр частот транспонированных колебаний.

2. Рассчитать при w=w _n значении АЧХ дискретной системы, рассматривая в качестве входного сигнала помеху f ( t ), а выходного e ( t ). Для этого:

а) определить передаточную функцию ;

б) найти АФЧХ ;

в) найти значение .

Расчет производить при значениях k₁ и k₂, обеспечивающих протекание в системе переходных процессов конечной деятельности (см. лаб. №2).

3. При В = 10 рассчитать амплитуды основной, транспонированных составляющих на выходе системы, для чего:

а) определить величину A_0;

б) рассчитать АЧХ непрерывной части

;

в) в соответствии с (9) найти величину А_у (w _T).

4. Выбрать параметр Т_ф непрерывного корректирующего фильтра , обеспечивающего десятикратное ослабление амплитуды помехи:

Дата добавления: 2019-01-14; просмотров: 146; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 Следующая ⇒

Мы поможем в написании ваших работ!