Рівняння кривих другого порядку
Відомі точки: . Обчислити координати векторного добутку . 16. Відомі вектори . Визначити координати векторного добутку 17. Відомі вершини трикутника Визначити зовнішній кут при вершині C. 18. Знайти вектор який колінеарний вектору і задовольняє умову 19. Дано вершини піраміди . Знайти висоту, проведену з вершини . 20. Знайти проекцію вектора на вісь, що складає з координатними осями рівні кути.
III. Аналітична геометрія
Пряма на площині
Задача 3.1. Визначити, які з точок 
та 
лежать на прямій 
, а які не лежать на ній.
Розв’язання. Точка лежить на прямій тоді і тільки тоді, коли її координати задовольняють рівняння прямої. Підставимо координати 
в рівняння прямої. Одержимо 
, значить ця точка лежить на прямій.
Тепер підставимо координати 
: 
, значить прямій не належить.
Задача 3.2. Визначити точки перетину прямої 
з координатними осями та накреслити цю пряму.
Розв’язання. На осі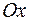 
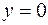, тому 
, значить точкою перетину з віссю 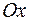є 
.
На осі 
, тому 
, значить точкою перетину з є 
.
Для побудови прямої зобразимо ці точки на координатній площині та проведемо через них пряму.
Задача 3.3. Знайти точку перетину двох прямих 
та 
.
Розв’язання. Координати точки перетину двох прямих повинні задовольняти двом рівнянням прямих одночасно, тому для знаходження точки перетину розв’яжемо систему 
.
Маємо 
. Значить 
, тобто точка перетину 
.
|
|
|
Задача 3.4. Дана пряма (l) 
. Скласти рівняння прямої, що проходить через точку 
1) перпендикулярно до даної прямої;
2) паралельно даній прямій.
Розв’язання. Зобразимо прямі на рисунку.
1) Позначимо шукану пряму (l1). Нормальний вектор до заданої прямої (l) можна знайти з її рівняння. Це вектор 
. Для шуканої прямої (l1) цей вектор є напрямним, тому для того, щоб записати її рівняння можна використати канонічне рівняння прямої
• 
,
де 
– точка, що належить прямій, а 
– напрямний вектор прямої.
У нашій задачі це рівняння набуде вигляду 
.
2) Позначимо шукану пряму (l2). Нормальний вектор заданої прямої (l) є нормальним і для шуканої прямої (l2). Тому, щоб записати рівняння цієї прямої, ми можемо скористатися наступною формулою:
• 
,
де – точка, що належить прямій, а 
– нормальний вектор прямої.
В нашому випадку рівняння набуде вигляду 
, або 
.
Задача 3.5. Дано вершини трикутника 
. Скласти рівняння:
1) висоти 
;
2) сторони 
;
3) медіани 
;
4) перпендикуляра 
опущеного з вершини 
на медіану .
Розв’язання. Зробимо креслення.
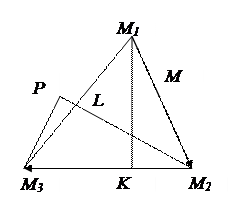
1) Нормальним вектором для висоти є вектор 
. Так як пряма проходить через точку , одержимо рівняння цієї прямої: 
, або 
.
|
|
|
2) Напрямним вектором для сторони є вектор 
. Тоді канонічне рівняння цієї прямої набуде вигляду 
.
3) Знайдемо координати точки 
, використовуючи формулу для знаходження координат середини відрізку. Маємо 
, тобто 
. Напрямний вектор медіани – це вектор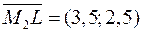 
. Тоді канонічне рівняння медіани: 
.
4) Вектор 
є нормальним для , тому рівняння цього перпендикуляра може бути записано у вигляді 
, 
або 
.
Задача 3.6. Знайти проекцію точки 
на пряму 
.
Розв’язання. Накреслимо рисунок.
Спочатку складемо рівняння прямої 
, яка проходить через точку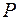 
перпендикулярно даній прямій. Нормальним вектором для даної прямої є вектор 
, і цей вектор є напрямним для прямої . Тому запишемо канонічне рівняння прямої : 
.
В результаті перетворень це рівняння набуде вигляду.
Шукана точка М є точкою перетину та , тому її координати знайдемо, розв’язавши систему
.
Маємо 
. Значить, координати точки 
.
Задача 3.7. Дано рівняння двох сторін прямокутника 
, 
та рівняння його діагоналі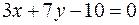 
. Скласти рівняння інших двох сторін цього прямокутника.
Розв’язання. Зобразимо рисунок.
Відразу помітимо, що дві задані прямі паралельні, оскільки мають однакові нормальні вектори, тому представляють протилежні сторони прямокутника, наприклад 
і 
.
|
|
|
Точка 
є точкою перетину і діагоналі 
, тому знайдемо її координати, розв’язавши систему рівнянь.
;
, тобто 
.
Аналогічно знайдемо точку 
, як точку перетину та діагоналі .
;
, тобто 
.
Нормальним вектором для і є вектор 
. Цей вектор є напрямним для 
і 
. Тому рівняння цих сторін є:
; 
Задача 3.8. Знайти кут між прямими 
та 
.
Розв’язання. Нормальні вектори цих прямих мають координати 
і 
відповідно. Кут між прямими дорівнює куту між нормальними векторами, а косинус кута між векторами може бути знайдений за формулою
• 
.
Маємо 
. Отже, кут між прямими 
.
Задача 3.9. Визначити, при якому значенні 
дві прямі 
, 
паралельні та перпендикулярні.
Розв’язання. Нормальні вектори для цих прямих мають координати 
і 
відповідно.
• Дві прямі перпендикулярні, коли їх нормальні вектори ортогональні, тобто скалярний добуток цих векторів має дорівнювати нулю.
Обчислимо скалярний добуток: 
. З цього рівняння 
.
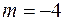Дві прямі паралельні, коли їх нормальні вектори колінеарні. Умовою колінеарності векторів є пропорційність їх координат. Запишемо цю умову для наших нормальних векторів: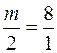 
, значить 
.
|
|
|
Задача 3.10. Знайти відстань між двома паралельними прямими 
та 
.
Розв’язання. Зобразимо рисунок.
Знайдемо одну точку на прямій 
. Для цього в її рівняння підставимо 
. Одержимо 
, тобто точка на прямій 
. Перетворимо рівняння другої прямої, перенісши всі доданки в ліву частину рівності: 
.
Відстань між двома прямими – це відстань від точки 
до прямої 
.
• Відстань від точки до прямої 
обчислюється за формулою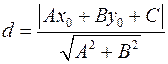 
.
В нашому випадку 
.
Задачі для самостійної роботи
1. Записати рівняння прямої з кутовим коефіцієнтом, якщо їй належать точки 
2. Задано вершини трикутника: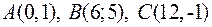 
. Знайти рівняння висоти, що проведена із вершини С.
3. Довести, що прямі 
паралельні і обчислити відстань між ними.
4. Дано точки: 
Скласти рівняння прямої, яка проходить через середину відрізка AB перпендикулярно цьому відрізку.
5. Обчислити площу трикутника, який відтинається прямою 
від координатного кута.
6. Обчислити відстань від точки 
до прямої 
7. Визначити кут між двома прямими 
.
8. Скласти рівняння сторін та медіан трикутника з вершинами 
, 
, 
.
9. Дано дві точки 
та 
. Скласти рівняння прямої, що проходить через точку Q перпендикулярно до відрізку PQ.
10. Через точки 
та 
проведено пряму. Визначити точки перетину цієї прямої з осями координат.
11. Знайти рівняння прямої, яка проходить через точку перетину прямих 
і 
та точку 
.
12. Подані дві вершини трикутника 
: 
, 
та точка 
перетину його висот. Знайти вершину 
.
13. Знайти рівняння прямої, яка проходить через точку 
паралельно прямій 
, якщо 
, 
.
14. Знайти точку, симетричну точці 
відносно прямої 
.
15. Знайти точку 
перетину діагоналей чотирикутника 
, якщо 
, 
, 
, 
.
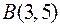16. Відомі рівняння сторони трикутника 
, його висот 
: 
та 
: 
. Знайти рівняння двох інших сторін трикутника .
17. Скласти рівняння висоти, яка проведена через вершину 
трикутника 
, якщо відомі рівняння його сторін: 
, 
, 
.
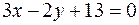18. Дано трикутник з вершинами 
, 
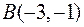та 
. Знайти рівняння та обчислити довжину його медіани, яка проведена з вершини 
.
19. Знайти рівняння перпендикулярів до прямої 
, які проведені через точки перетину даної прямої з осями координат.
20. Записати рівняння прямої, яка проходить через точку 
та утворює з віссю 
кути: а) 
, б) 
, в) 
.
21. Яку координату має точка , яка лежить на одній прямій з точками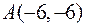 
та 
та має абсцису, рівну 
?
22. Відомі рівняння двох сторін ромба 
та 
та рівняння однієї з його діагоналей 
. Знайти рівняння другої діагоналі.
23. Задано рівняння висот трикутника 
, 
та координати його вершини 
. Знайти рівняння сторін 
та трикутника.
24. Подані рівняння двох сторін паралелограма 
, 
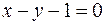та точка перетину його діагоналей 
. Знайти рівняння двох інших сторін.
Рівняння кривих другого порядку
Задача 3.11. Скласти рівняння еліпса, фокуси якого розташовані на осі абсцис симетрично щодо початку координат, якщо відомі:
1) 
–точка на еліпсі та 
– мала піввісь;
2) 
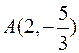– точка на еліпсі, 
– ексцентриситет.
Розв’язання.
1)
• Канонічне рівняння еліпса має вигляд: 
.
Підставимо у це рівняння замість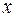 
та 
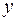координати точки А, а також дане значення 
. Одержимо рівняння 
. Розв’яжемо його:
Отже відповідь: 
.
2) З умови задачі маємо 
, отже 
. З другого боку, підставимо у канонічне рівняння координати точки А. Одержимо систему рівнянь 
. Звідси
,
отже відповідь: 
.
Задача 3.12. Скласти рівняння гіперболи, фокуси якої розташовані на осі абсцис симетрично щодо початку координат, якщо відомі:
1) 
– рівняння асимптот, 
– відстань між вершинами;
2) 
– точки на гіперболі.
Розв’язання.
1)
• Канонічне рівняння гіперболи має вигляд: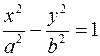 
.
Оскільки рівняння асимптот задаються формулами 
, з умови задачі одержимо:
.
Отже відповідь: 
.
2) Підставимо координати обох точок у рівняння гіперболи. Одержимо систему рівнянь 
. В результаті заміни 
прийдемо до системи лінійних рівнянь 
, яку можна розв’язати за правилом Крамера.
Тоді 
, значить 
.
Отже, відповідь: 
.
Задача 3.13. Скласти рівняння параболи, вершина якої знаходиться у початку координат, якщо відомо:
1) парабола симетрична відносно осі 
та проходить через точку 
;
2) 
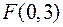– фокус параболи.
Розв’язання.
1)
• Канонічне рівняння параболи має вигляд 
.
Підставимо у це рівняння координати точки А. Маємо 
. Отже відповідь: 
.
2) Оскільки координати фокуса задаються формулою 
, то 
. Отже відповідь: 
.
Задача 3.14. Привести до канонічного вигляду рівняння кривої другого порядку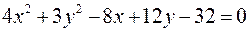 
та зобразити цю криву на рисунку.
Розв’язання. Виконаємо перетворення заданого рівняння.
Дане рівняння задає еліпс. Тепер зобразимо криву на рисунку. Центром симетрії еліпса буде точка 
.
Задача 3.15. Привести до канонічного вигляду рівняння кривої другого порядку та зобразити цю криву на рисунку:
1) 
;
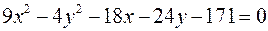2) 
.
Розв’язання.
1) Виконаємо перетворення заданого рівняння.
Дане рівняння задає гіперболу. Тепер зобразимо криву на рисунку. Центром симетрії гіперболи буде точка 
. Гілки гіперболи напрямлені вздовж осі 
.
 |
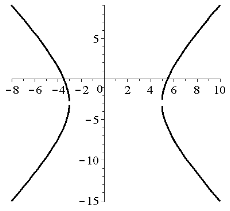
2) Виконаємо перетворення заданого рівняння.
Дане рівняння задає гіперболу. Тепер зобразимо криву на рисунку. Центром симетрії гіперболи буде точка 
. Гілки гіперболи напрямлені вздовж осі 
.
Задача 3.16. Привести до канонічного вигляду рівняння кривої другого порядку та зобразити цю криву на рисунку:
1) 
;
2) 
.
Розв’язання.
1) Виконаємо перетворення заданого рівняння.
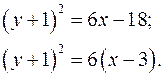
Дане рівняння задає параболу. Тепер зобразимо криву на рисунку. Вершиною параболи буде точка 
. Гілки параболи направлені вздовж осі вправо.
2) Виконаємо перетворення заданого рівняння.
Дане рівняння задає параболу. Тепер зобразимо криву на рисунку. Вершиною параболи буде точка 
. Гілки параболи направлені вздовж осі вниз.
Задача 3.17. Привести до канонічного вигляду рівняння кривої другого порядку та зобразити цю криву на рисунку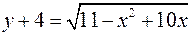 
.
Розв’язання. Піднесемо обидві частини рівності до квадрату, попередньо помітивши, що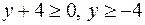 
. Одержимо
Дане рівняння задає коло. Центром кола буде точка 
. Однак тепер слід врахувати обмеження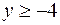 
. Воно означає, що вихідна рівність задає лише верхню половину кола. На рисунку крива виглядає наступним чином:
 |
Задачі для самостійної роботи
1. Еліпс, симетричний відносно осей координат, проходить через точки 
. Записати його канонічне рівняння.
2. Знайти рівняння і побудувати гіперболу якщо відстань між її директрисами дорівнює 
, а ексцентриситет 
.
3. Ордината точки на параболі 
дорівнює 6. Знайти відстань від цієї точки до фокуса. Побудувати параболу, її фокус і директрису.
4. Скласти рівняння еліпса, симетричного відносно осей координат, якщо йому належить точка 
і відстань між фокусами дорівнює 8.
5. Привести рівняння кривої другого порядку до канонічного вигляду та зробити креслення
1) 
;
2) 
.
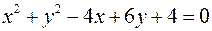Дата добавления: 2018-11-24; просмотров: 96; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!