Случайные процессы в системах автоматического управления.

Численное решение дифференциальных уравнений

Ранее было отмечено, что физические процессы удобно моделировать с помощью уравнений состояний, имеющих вид:

где x – n x 1-вектор состояний с начальным условием α; p – n x 1-вектор параметров;

u – q x 1-вектор управлений; t – n x 1-вектор-функция; t-переменная текущего времени.

Численное решение обыкновенных дифференциальных уравнений – важный этап работы системы цифрового управления. Разберем методы решения двух типов – методы предсказания и коррекции и методы Рунге-Кутта.

Методы предсказания и коррекции используют конечно-разностные формулы интегрирования. Это возможно потому, что решение уравнений можно найти, оценивая интегралы вида:

В методах предсказания и коррекции последующее состояние предсказывается по формуле, использующей известные значения. При коррекции для улучшения оценки используются предсказанная информация. Примером пары формул предсказания – коррекции служат формулы Адамса и Бешфорта:

где

Связь с конечно-разностными формулами интегрирования можно установить, сравнивая уравнения. Формула коррекции подробнее рассматривается в задаче 1.

Методы предсказания часто предпочитают другим методам, так как они требуют меньшего числа оценок функций, кроме того ошибка приближения при этом оценивается более точно . Методы предсказания - коррекции имеют несколько недостатков: они не могу работать до тех пор, пока не произведена оценка некоторого числа состояний, равного порядку разностей; трудно изменять размер шага интегрирования h; они точны только в тех Случаях, когда функция f гладкая и непрерывная, тогда как в задачах управления функция f часто бывает разрывной, например при переключении знака управления.

Здесь рассматриваются также методы Рунге - Кутта. Эти

методы не требуют знания начальных состояний, и, если принять меры предосторожности, их можно применять к функциям с непрерывными производными. Кроме того, в этих случаях легко изменять размер шага интегрирования.

Простейшей схемой тина Рунге - Кутта является первый член разложения в ряд Тейлора по х

Разложение в ряд Тейлора можно производить с системам любого порядка. Наиболее распространенной является схема Рунге - Кутта четвертого порядка, но ради простоты МЫ рассмотрим: схему второго порядка. При этом будет показано, каким образом на основании тех же соображений можно получить схему четвертого порядка. Запишем в виде х = f (х, t), где параметр р входит в f, а функция u учтена явной зависимостью f от t.

Разлагая х (t + h) в ряд Тейлора второго порядка относительно х (t), находим, что i-ю компоненту х (t + h) можно выразить с по мощью тензорных обозначений Эйнштейна для немых индексов:

Определим множество векторов

в линейную форму разложения

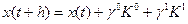
где γ и γ - константы.

Путем подстановки выражений, находим

Раскладывая правую часть уравнения в ряд Тейлора относительно f(x, t), получаем i-ю компоненту:

Приравнивая соответствующие коэффициенты всех независимых производных f, получаем

В этом случае уравнений меньше, чем неизвестных, и одним из возможных решений является

Подставляя эти константы, получаем алгоритм Рунге-Кутта второго порядка:

Путем аналогичных рассуждений можно показать, что алгоритм Рунге - Кутта четвертого порядка имеет вид

Стандартный процесс Рунге-Кутта имеет следующее множество параметров:

Значения параметров процесса второго порядка не единственны, и в некоторых приложениях можно добиться определенных преимуществ, используя множество параметров, отличное от приведенного выше. Однако в общем случае приведенный набор параметров оказывается удовлетворительным.

Ошибка для процесса Рунге-Кутта четвертого порядка определяется членом пятой степени в разложении Тейлора, но в общем случае ее трудно оценить.

Естественно, возникает вопрос о том, какое преимущество имеет (и имеет ли) процесс Рунге - Кутта четвертого порядка по сравнению с простым процессом первого порядка. Из формул видно, что для процесса четвертого порядка требуется примерно в 4 раза больше вычислений, чем для процесса первого порядка. Однако приведенный ниже пример показывает, что допустимый размер шага для процесса четвертого порядка при заданной величине ошибки может быть в сотни раз больше, чем для процесса первого порядка.

В качестве примера рассмотрим уравнение первого порядка, поскольку это облегчает вычисление различных ошибок усечения.

Пример 1.8 Составить схемы вычисления x(t+h) через x(t)

при

Процесс Рунге-Кутта первого порядка дает

, ошибка

Процесс Рунге-Кутта четвертого порядка дает

, ошибка

Размер шага при заданной ошибке показан в таблице. Ошибки возникают в различные моменты времени, но, поскольку в общем случае процесс продолжается на большом интервале времени, например при управлении, значение имеет абсолютная ошибка на каждом шаге.

Заданная допустимая ошибка
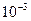
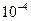
Максимальный размер шага в процесс Рунге-Кутта первого порядка Максимальный размер шага в процессе Рунге-Кутта четвертого порядка	0,445 1,644	0,141 1,037	0,0445 0,654	0,014 0,412	0,0014 0,164

В таблице показано, что процесс четвертого порядка более эффективен по сравнению с процессом первого порядка. Обычно используются схемы не выше четвертого порядка, так как схемы высших порядков более сложны.

Пример 1.9 Напишем стандартную подпрограмму для численного интегрирования множества векторных дифференциальных уравнений вида:

а. Используйте алгоритм Рунге-Кутта четвертого порядка.

б. Включите подпрограмму дифференциальных уравнений так, чтобы их можно было менять по желанию.

в. Обеспечьте возможность изменения числа уравнений.

г. Отладьте программу, проинтегрировав уравнения

Эти уравнения описывают свободное движение вращающегося твердого тела. Здесь переменные Х1 Х2 Х3 - составляющие угловой скорости относительно главной оси, А, В и С – соответствующие главные моменты инерции и Е – показатель затухания.

Положите А=1, В=2, С=3, Е=0.2, Х1(to)=1, Х2(to)=1, Х3(to)=0. Используйте шаг h=0.1c. (Проверьте Х1(1,0)=0,9382328, Х2(1,0)=0,7705584, Х3(1,0)=0,2770832

//////////////////////////////////////////////////////////////////////////

// Файл: diff2.cpp

// Описание: Интегрирование системы дифф. ур.

// Зависимости: Стандарт С++

// Авторы: XXX

//////////////////////////////////////////////////////////////////////////

#include <math.h>

#include <stdio.h>

#include "Integrator.h"

/// Класс реализация модели (диф.ур.)

class CDiff2: public Integrator

{

protected:

double X[3]; ///< Переменные интегрирования

double t; ///< Время

public:

/// Конструктор

CDiff2()

{

Integrator::PreInitialize(3);

ODE_LEFT(0,X[0]); // Указание интегрируемых переменных

ODE_LEFT(1,X[1]);

ODE_LEFT(2,X[2]);

ODE_TIME(t); // Время

}

/// Реализация функции правых частей

bool Right()

{

try

{

double A = 1.;

double B = 2.;

double C = 3.;

double E = 0.2;

ODE_RIGHT(0) = (C/A-B/A)*XT(1)*XT(2) - (E/A)*XT(0); // Правые части

ODE_RIGHT(1) = (A/B-C/B)*XT(2)*XT(0) - (E/B)*XT(1);

ODE_RIGHT(2) = (B/C-A/C)*XT(0)*XT(1) - (E/C)*XT(2);

}

catch(...)

{

return false;

}

return true;

}

// Инициализация модели

void Initialize(double X1,double X2,double X3,double _t)

{

X[0] = X1;

X[1] = X2;

X[2] = X3;

t = _t;

}

// Опрос состояния

bool GetState(double& X1,double& X2,double& X3,double& _t) const

{

X1 = X[0];

X2 = X[1];

X3 = X[2];

_t = t;

return true;

}

bool Step()

{

return RK4Step();

}

};

// Испльзование CDiff2 и сохранение результатов в файл

void main()

{

FILE* fd; // Файловая переменная

fd = fopen("Result.txt","w"); // Отрытие файла для сохранения результатов

double X1,X2,X3,t; // Переменные состояния и время

CDiff2 diff1; // Класс - модель

X1 = 1.; // Начальные условия

X2 = 1.;

X3 = 0.;

t = 0.;

diff1.Initialize(X1,X2,X3,t); // Инициализация модели

diff1.SetStep(0.1); // Установка шага интегрирования

fprintf(fd,"%lf %lf %lf %lf\n",t,X1,X2,X3); // Сохранение состояния

while(t<=1.) // Условие окончания интегрирования

{

diff1.Step(); // Шаг

diff1.GetState(X1,X2,X3,t); // Опрос состояния

fprintf(fd,"%lf %lf %lf %lf\n",t,X1,X2,X3); // Сохранение состояния

}

fflush(fd); // Слив буферов потока

fclose(fd); // Закрытие файла

}

#ifndef __INTEGRATOR__

#define __INTEGRATOR__

//////////////////////////////////////////////////////////////////////////

// Файл: Integrator.h

// Описание: Класс для интегрирования обыкн. диф.ур. (ODE)

// Версия файла: 1.0.0.1

// Зависимости: Стандарт С++

// Авторы: Костюков В.В.

//////////////////////////////////////////////////////////////////////////

// Протокол изменений:

//////////////////////////////////////////////////////////////////////////

// Макрос связывает переменную вектора состояния P

// с N-ым элеменом массива интегрируемых переменных

// (Left Part of ODE)

#define ODE_LEFT(N,P) m_ppParam[N] = &(P)

// Макрос связывает (указывает) переменную времени Р

// (Left Part of ODE)

#define ODE_TIME(P) m_pTime = &(P)

// Макрос предоставляет доступ к вектору правых частей

// (Right Part of ODE)

#define ODE_RIGHT(N) m_pRight[N]

// Класс реализующий интегрирование системы диф.ур-ий (ODE)

// Для интеграции уравнений необходимо:

// 1. Cоздать производные от Integrator класс,

// 2. Указать в конструкторе производного класса переменные интегрирования

// и параметр времени при помощи макросов ODE_LEFT, ODE_TIME

// 3. Реализовать виртуальную функцию Right,

// в теле функции определить вычисление правых частей,

// (испоользовать макрос ODE_RIGHT)

/// Класс для интегрирования обыкн. диф.ур.

class Integrator

{

private:

bool m_bInit; ///< Признак инициализации модели

double a[5]; ///< Коэфициенты РК-4

double *m_pDX; ///< ... для РК-4

protected:

double **m_ppParam; ///< Вектор указателей на интегрируемые параметры

double *m_pRight; ///< Вектор правых частей ( расчитывается в Right() )

double *m_pTime; ///< Параметр времени

double m_dT; ///< Шаг интегрирования

unsigned long m_nDim; ///< Размер вектора состояния

double *m_pXT; ///< ... для РК-4

public:

Integrator()

{

a[0] = 0.5;

a[1] = 0.5;

a[2] = 1.0;

a[3] = 1.0;

a[4] = 0.5;

m_dT = 0.01;

m_nDim = 0;

m_bInit = false;

}

~Integrator()

{

if(m_bInit)

{

delete[] m_ppParam;

delete[] m_pRight;

delete[] m_pXT;

delete[] m_pDX;

}

/// Инициализация интегратора

virtual bool PreInitialize(unsigned long nDim)

{

if(m_bInit) return false;

if(nDim>0) m_nDim = nDim;

else return false;

m_ppParam = new double*[m_nDim];

m_pRight = new double[m_nDim];

m_pXT = new double[m_nDim];

m_pDX = new double[m_nDim];

m_bInit = true;

return m_bInit;

}

/// Функция расчета правых частей ODE

virtual bool Right() {return true;}

/// Задать шаг интегрирования

bool SetStep(const double dT)

{

if( m_dT>0 )

{

m_dT = dT;

return true;

}

return false;

}

/// Опросить шага интегрирования

double GetStep() const

{

return m_dT;

}

/// Методы интегрирования

protected:

//////////////////////////////////////////////////////////////////////////

// Макроопределения для удобства записи алгоритмов интегрирования

#define X(i) *(m_ppParam[i])

#define DX(i) m_pDX[i]

#define XT(i) m_pXT[i]

#define DXT(i) m_pRight[i]

#define time *m_pTime

#define dt m_dT

#define N m_nDim

/// Шаг интегрирования методом Эйлера

bool EilerStep()

{

if(!m_bInit) return false;

try

{

unsigned int i;

if(!Right()) throw 0;

for(i = 0;i < N; i++)

{

X(i) += DXT(i)*dt;

}

time += dt;

}

catch(...)

{

return false;

}

return true;

}

/// Шаг интегрирования методом Рунге-Кутта 4-го порядка

bool RK4Step()

{

if(!m_bInit) return false;

try

{

double h = dt;

double t;

double b,c;

unsigned int i,j;

for(i = 0;i < N; i++)

{

DX(i) = 0;

XT(i) = X(i);

}

t = time;

for(j = 0;j < 4; j++)

{

if(!Right()) throw 0;

b=a[j+1];

c=a[j];

t=time+c*h;

for(i = 0;i < N; i++)

{

DX(i) += b*h*DXT(i)/3.;

XT(i) = X(i) + c*h*DXT(i);

}

for(i = 0;i < N; i++)

{

X(i) += DX(i);

}

time += dt;

}

catch(...)

{

return false;

}

return true;

}

// Очистка макроопределений

#undef X

#undef DX

#undef DXT

#undef time

#undef dt

////////////////////////////////////////////////////////////////////

};

#endif //__INTEGRATOR__

Случайные процессы в системах автоматического управления.

Как уже отмечалось процессы бывают детерминированными то есть наблюдение дает возможность предсказать дальнейшее поведение. Индетерминированные процессы. Сколько не наблюдаем, не знаем как прогнозировать. Случайные процессы (промежуточные процессы). Точно предсказать не можем. Есть механизм, который не знаем (скрытый параметр), но можем найти некоторые характеристики, которые позволяют описывать общие свойства в поведении процесса.

Эти характеристики знает только Господь Бог. У случайных процессов характеристики являются неслучайными. Но мы их находим из экспериментов, поэтому они точно быть выявлены не могут. Говорят, что для описания процессов используются оценки (случайные числа)

Теория оценивания занимается нахождением этих характеристик.

Там есть требования :

- несмещенность

- состоятельность

- эффективность

Наиболее общим описанием случайных параметров является многомерные законы распределения случайных процессов. Случайные процессы в любой момент времени является случайной величиной. Значение процессов в различные моменты времени связанны. Степень взаимосвязи может быть разной. Если задан n-мерный закон распределения, то считается, что случайный процесс полностью задан. К сожалению, пользоваться законами распределения очень затруднительно из-за громоздкости и слабой обозримости. Поэтому в технике, пытаясь сократить громоздкость, не пытаются максимально точно изучать случайные процессы, а используют их для получения оценок в конкретных технических задачах. Одной из самых главных задач для систем управления - это оценить величину ошибки, которая появляется из-за того, что тот процесс является случайным. Как выбрать параметр системы, чтобы ошибка была минимальной?

Такие две задачи удается решать и без полного описания. Поэтому есть раздел «Корреляционная теория случайных процессов»

Общие понятия

Наиболее общим и полным описанием является n-мерный закон :

P( )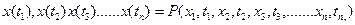

Являющийся функцией 2-х переменных:

x₂x₃

t₁ t₂ t₃ t₄ t_N

N моментов времени

N значений x

Удобнее пользоваться не законами вероятность, а плотностью вероятности.

Стационарные процессы - это процессы, у которых при описании случайных процессов, то есть при задании законов распределения, существует свойство: абсолютное значение времени на вид закона не влияет. Играет роль только относительное расположение точек t_1,t_2,…t_n_.

- операция стационарности в узком смысле слова.

Наличие стационарности упрощает вид многих форму. Достаточно знать только расстояние между точками (сдвиг).

Эргодичность процесса.

При первой возможности пытаются трактовать так: эргодичность означает, что вычисление характеристики по ансамблю можно заменить вычислением характеристики по реализации. Существует тест на эргодичность.

Многие процессы не являются стационарными. Их пытаются все описывать как стационарные, а учитывают нестационарность специальными дополнительными вычислениями.

Одномерная плотность распределения вероятности.

- вероятность того, сколько траекторий прошло через диапазон , к общему числу траекторий.

Двумерный закон распределения

Итого получается, смотри **

Процессы, у которых идет учет значений только для одного предыдущего момента вращения, называются марковскими.

Для решения ряда технических задач можно обойтись моментными характеристиками.

Самыми важными моментными характеристиками являются первые и вторые, начальные и центральные моменты. Теория, которая оперирует только с первыми и вторыми начальными и центральными моментами, называется корреляционной теорией.

1. Начальный момент – математическое ожидание

2. Второй момент – дисперсия

D(t)=

3. Корреляционная функция

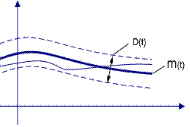
Математическое ожидание оценивает среднее значение процесса.

Дисперсия оценивает разброс относительно математического ожидания.

Корреляционная функция характеризует степень линейной взаимосвязанности между случайной производной по времени. Если корреляционная функция такова, что она уменьшается у одного процесса для одних и тех же сдвигов момента времени, больше, чем у другого процесса, то это значит, что данный процесс имеет меньшую степень взаимосвязанности.

Если выполняется гипотеза эргодичности и процессы стационарные, то получается, что процесс не зависит от абсолютного значения момента времени, одномерная плотность распределения будет одинакова для любого t₁ момента времени : p(x₁). Двумерная плотность зависит лишь от разности моментов времени (сдвига : 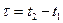) : p(x₁,x₂,t).

1. Математическое ожидание

По гипотезе стационарности : m

По гипотезе эргодичности :

2. Не зависит от времени дисперсия (стационарность и эргодичность) :

_4.Если процесс стационарный, играет роль только разница между t₁ и t₂

k – дискретный сдвиг

t- шаг выборки процесса.

Если сдвига нет, то получается дисперсия.

Примеры: Гауссовы законы плотности распределения случайного процесса

здесь: k₁(t₂-t₁) , k₂(t₂-t₁) , k₃(t₂-t₁) некоторые функции.

В последней плотности распределения указан конкретный вид функций k₁ , k₂ , k₃.

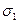
Корреляционная теория для гауссовских законов является исчерпывающей. Зная корреляционные функции, можно записать закон распределения.

k_, k₁, k₂ соответствуют корреляционным функциям.

В следующем примере (3-я строка) уточнение, один из конкретных видов. Если закон не Гаусса, то данная теория является первым приближением и решение является точным до вторых моментов.

;

Дата добавления: 2018-11-24; просмотров: 265; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!