Координати вектора. Лінійні операції над векторами
Міністерство освіти і науки України
Одеський національний морський університет
Кафедра «Вища та прикладна математика»
Практичні заняття з вищої математики
(Частина 1)
Навчальний посібник
Одеса - 2010
Навчальний посібник склали Кирилов Сергій Олександрович – кандидат фізико-математичних наук, доцент кафедри «Вища та прикладна математика» ОНМУ, Кирилова Людмила Олександрівна – кандидат фізико-математичних наук, доцент кафедри математичних методів аналізу економіки ОДЕУ та Кирилова Ольга Іванівна – асистент кафедри вищої математики ОНМА.
Методичні вказівки схвалені на засіданні кафедри «Вища та прикладна математика» ОНМУ 5 листопада 2010 р. (протокол № 3).
Рецензенти: д.ф.-м. н., проф. Андронов І.Л.;
| |
Вступ
Даний навчальний посібник призначений для студентів 1 курсу ФТТС ОНМУ, які вивчають дисципліну „Вища математика”, а також може бути корисним студентам інших факультетів.
Посібник містить зразки розв’язань більше ніж 100 задач, які охоплюють всі теми курсу вищої математики, що розглядаються у перших двох модулях.
Автори не ставили метою наводити у посібнику довідковий матеріал з тем, які вивчаються. Такий матеріал легко знайти у будь-якому підручнику з вищої математики та в навчальних посібниках, які розроблені викладачами кафедри „Вища та прикладна математика” ОНМУ з усіх тем курсу. У той же час автори намагались подавати розв’язання досить детально, тому необхідні для розв’язання задач формули та математичні факти часто вміщені прямо в тексті та помічені значком •, щоб привернути увагу читача.
|
|
|
Розташування параграфів у навчальному посібнику відповідає діючий програмі. Перші задачі параграфа розв’язуються, як правило, більш детально, ніж наступні. Відповідно, для найбільшої ефективності роботи вивчати розв’язання задач слід підряд. Проте це не виключає використання посібника в якості довідника, оскільки в посібнику розібрано велику кількість типових задач, що зустрічаються в типових розрахунках з тем курсу та традиційно виносяться на контрольні та екзамени. Наприкінці кожного параграфу міститься декілька задач для самостійного розв’язання.
I. Елементи лінійної алгебри
Визначники
Задача 1.1. Обчислити визначник 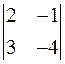 .
.
Розв’язання.
• Формулу для обчислення визначника другого порядку зручно запам’ятовувати за допомогою наступної діаграми:

Обчислимо заданий визначник.
 .
.
Задача 1.2. Обчислити визначник, використовуючи правило трикутників  .
.
Розв’язання.
|
|
|
• Для запам’ятовування правила трикутників обчислення визначника третього порядку використаємо наступну діаграму

Обчислимо заданий визначник.

Задача 1.3. Обчислити визначник, використавши формулу розкладання визначника за елементами рядка або стовпця  .
.
Розв’язання. Для обчислення цього визначника зручно розкладати його або за другим рядком, або за третім стовпчиком, оскільки в них є нульовий елемент. Ми використаємо для обчислення розкладання за другим рядком.
 .
.
Задача 1.4. Виконати дії над матрицями
 ,
,  ,
,  :
:
1)  ;
;
2) 
Розв’язання.
1)

2) Знайдемо  . Для цього віднімемо відповідні елементи заданих матриць.
. Для цього віднімемо відповідні елементи заданих матриць.
 .
.
Далі виконаємо множення. Оскільки матриці мають розміри  та
та  множення можливе, причому матриця, отримана в результаті, буде мати розміри
множення можливе, причому матриця, отримана в результаті, буде мати розміри  .
.

Задача 1.5. Обчислити  , де
, де 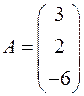 .
.
Розв’язання. Транспонована матриця для матриці А буде мати вигляд  . Далі виконаємо множення. Оскільки матриці мають розміри
. Далі виконаємо множення. Оскільки матриці мають розміри  та
та  множення можливе, причому матриця, отримана в результаті, буде мати розміри
множення можливе, причому матриця, отримана в результаті, буде мати розміри  .
.

Задача 1.6. Знайти обернену матрицю 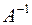 для матриці
для матриці
 .
.
Розв’язання.
• Обернену матрицю знайдемо за формулою
 .
.
Спочатку обчислимо визначник заданої матриці.
|
|
|

Оскільки визначник не дорівнює нулю, дана матриця має обернену. Далі ми знайдемо приєднану матрицю. Для цього обчислимо алгебраїчні доповнення елементів матриці А.
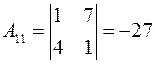 ,
,  ,
,  ,
,
 ,
,  ,
,  ,
,
 ,
,  ,
,  .
.
Отже, приєднана матриця має вигляд  .
.
Одержимо
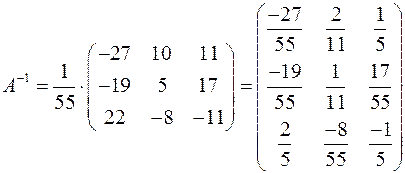 .
.
Задачі для самостійної роботи
1. Обчислити визначник  .
.
2. Обчислити визначник  .
.
3. Обчислити визначник  .
.
4. Обчислити визначник  .
.
5. Знайти  якщо
якщо 
6. Дано дві матриці  та
та  . Знайти
. Знайти  .
.
7. Знайти добуток  .
.
8. Перемножити матриці  .
.
9. Побудувати обернену матрицю для матриці 
10. Побудувати обернену матрицю для матриці  .
.
Системи лінійних рівнянь
Задача 1.7. Розв’язати систему рівнянь, використовуючи правило Крамера  .
.
Розв’язання. Обчислимо головний визначник системи.

Головний визначник системи не дорівнює нулю, тому система сумісна та має єдиний розв’язок. Знайдемо допоміжні визначники.



За формулами Крамера знаходимо розв’язок системи
 .
.
Задача 1.8. Розв’язати систему за методом Гауса  .
.
Розв’язання. Метою перетворень, які виконуються при розв’язанні системи методом Гауса є приведення системи до трикутного вигляду, тобто до системи, в якій всі коефіцієнти, розташовані під головною діагоналлю, дорівнюють нулю. З цією метою ми, по-перше, переставимо третє рівняння на перший рядок. Це рівняння ми вибрали тому, що з усіх рівнянь у нього найменший за модулем коефіцієнт при  .
.
|
|
|
 .
.
По-друге, перетворимо друге та третє рівняння наступним чином. До другого рівняння додамо перше, помножене на -3; до третього рівняння додамо перше, помножене на -2. Одержимо
 .
.
Ми досягли того, що у другому та третьому рівняннях коефіцієнти при  дорівнюють нулю. Тепер до третього рівняння додамо друге, помножене на -3. Маємо
дорівнюють нулю. Тепер до третього рівняння додамо друге, помножене на -3. Маємо
 .
.
Система записана у трикутному вигляді. Тепер із третього рівняння знаходимо  , далі з другого рівняння
, далі з другого рівняння

та, нарешті, з першого рівняння
 .
.
Задача 1.9. Розв’язати систему за методом Гауса  .
.
Розв’язання. Приведемо систему рівнянь до трикутного вигляду за допомогою перетворень, аналогічних тим, які використовувались при розв’язанні попередньої задачі.
 ;
;  ;
;
 .
.
Останнє рівняння з системи можна виключити. Тепер маємо систему, у якій при трьох невідомих залишилось лише два рівняння. Це означає, що наша система має нескінчену кількість розв’язків.
Подальша мета полягає в тому, щоб одержати формули, за якими всі ці розв’язки можливо знайти. Для цього назвемо змінну  вільною змінною і перенесемо доданки з цією змінною у праві частини обох рівнянь.
вільною змінною і перенесемо доданки з цією змінною у праві частини обох рівнянь.
 .
.
Тепер виразимо  та
та  через вільну змінну
через вільну змінну  . Маємо
. Маємо  ,
, 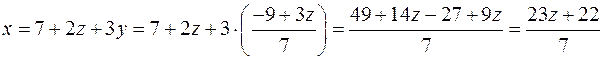 . Відповідь даної системи має вигляд:
. Відповідь даної системи має вигляд:  .
.
Задача 1.10. Розв’язати систему за методом Гауса
 .
.
Розв’язання. Приведемо систему до трикутного вигляду. Спочатку переставимо друге рівняння на перший рядок.
 .
.
Далі маємо
 ;
;  ;
;
 .
.
Останнє рівняння не може виконуватись за будь яких значень змінних, тому задана система не має розв’язків, тобто несумісна.
Задача 1.11. Розв’язати систему за методом Гауса  .
.
Розв’язання. Оскільки праві частини всіх рівнянь даної системи дорівнюють нулю, задана система називається однорідною. Особливість такої системи полягає в тому, що вона не може бути несумісною. Хоча б один розв’язок, а саме, нульовий  , вона має завжди. Далі розв’язання такої системи провадиться повністю аналогічно розв’язанню неоднорідних систем.
, вона має завжди. Далі розв’язання такої системи провадиться повністю аналогічно розв’язанню неоднорідних систем.
Приведемо систему до трикутного вигляду.
 ;
;  .
.
Поділимо обидві частини другого рівняння на 2. Далі
 ;
;  .
.
Звідси випливає, що система має єдиний розв’язок  .
.
Задача 1.12. Розв’язати систему матричним методом
 .
.
Розв’язання. Введемо у розгляд матриці:  – матриця коефіцієнтів,
– матриця коефіцієнтів,  – стовпчик вільних членів та
– стовпчик вільних членів та 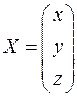 – стовпчик невідомих.
– стовпчик невідомих.
Спочатку обчислимо визначник матриці коефіцієнтів.

Оскільки цей визначник не дорівнює нулю, система сумісна та має єдиний розв’язок. Далі ми знайдемо приєднану матрицю. Для цього обчислимо алгебраїчні доповнення елементів матриці А.
 ,
,  ,
,  ,
,
 ,
,  ,
,  ,
,
 ,
,  ,
, 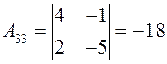 .
.
Отже, приєднана матриця має вигляд  .
.
• Тепер розв’язок системи знайдемо за формулою
 .
.
Одержимо
 .
.
Тобто  .
.
Задачі для самостійної роботи
1. Розв’язати за формулами Крамера 
2. Розв’язати за формулами Крамера  .
.
3. Розв’язати систему методом Гауса  .
.
4. Розв’язати систему методом Гауса  .
.
5. Розв’язати систему методом Гауса  .
.
6. Розв’язати систему методом Гауса  .
.
7. Розв’язати систему методом Гауса  .
.
8. Розв’язати систему рівнянь матричним методом  .
.
9. Розв’язати систему рівнянь матричним методом  .
.
10. Дослідити сумісність і знайти розв’язки системи  .
.
11. Дослідити сумісність і знайти розв’язки системи: 
II. Векторна алгебра
Координати вектора. Лінійні операції над векторами
Задача 2.1. Знайти модуль вектора  .
.
Розв’язання.
• Якщо вектор має координати  , то його модуль знаходиться за формулою
, то його модуль знаходиться за формулою 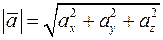 .
.
У нашому випадку  .
.
Задача 2.2. Дано дві точки  ,
,  . Знайти координати векторів
. Знайти координати векторів  і
і  .
.
Розв’язання.
• Нехай дано дві точки  ,
, 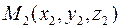 . Тоді координати вектора
. Тоді координати вектора  знаходяться як різниця координат кінця та початку цього вектора, тобто
знаходяться як різниця координат кінця та початку цього вектора, тобто  .
.
У нашій задачі  ,
,  .
.
Задача 2.3. Знайти напрямні косинуси вектора  .
.
Розв’язання.
• Для обчислення напрямних косинусів вектора  використовуємо формули
використовуємо формули
 .
.
Знайдемо  . Тоді
. Тоді
 .
.
Задача 2.4. Вектор складає з осями  та
та  кути
кути  та
та  відповідно. Який кут він складає з віссю
відповідно. Який кут він складає з віссю  ?
?
Розв’язання.
• Використаємо рівність
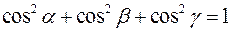 .
.
Тоді  ,
,
тобто 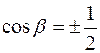 , значить
, значить 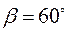 або
або  .
.
Задача 2.5. Дано два вектори  та
та  . Знайти координати векторів:
. Знайти координати векторів:
1)  ;
;
2)  .
.
Розв’язання.
• Якщо вектори  та
та  мають координати
мають координати 
 , то сума, різниця векторів та добуток вектора
, то сума, різниця векторів та добуток вектора  на число
на число  мають координати:
мають координати:
 ;
;
 ;
;
 .
.
1) Координати  , тоді
, тоді
 .
.
2) Координати  , тоді
, тоді
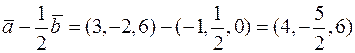 .
.
Задача 2.6. Знайти орт вектора  .
.
Розв’язання.
• Якщо  то орт
то орт  має координати
має координати
 ,
,
де  – напрямні косинуси вектора
– напрямні косинуси вектора  .
.
Тоді
 ,
,
а значить  .
.
Задача 2.7. Перевірити, що чотири точки 
 є вершинами трапеції.
є вершинами трапеції.
Розв’язання. Знайдемо координати векторів, які розташовані на сторонах чотирикутника  :
:  ,
,  ,
,  ,
,  .
.
• Два вектори  та
та  колінеарні, якщо
колінеарні, якщо
 .
.
У нашому випадку  , так як
, так як  . Значить дві сторони чотирикутника паралельні, тобто він є трапецією.
. Значить дві сторони чотирикутника паралельні, тобто він є трапецією.
Задача 2.8. Вектори  та
та  співпадають зі сторонами трикутника
співпадають зі сторонами трикутника  . Знайти координати векторів, прикладених до вершин трикутника та співпадаючих з його медіанами
. Знайти координати векторів, прикладених до вершин трикутника та співпадаючих з його медіанами  .
.
Розв’язання. Зобразимо трикутник  та його медіани та рисунку.
та його медіани та рисунку.

Добудуємо трикутник до паралелограму. За правилом паралелограма  , далі
, далі  , тоді координати
, тоді координати
 .
.
Знайдемо 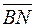 .
.

Обчислимо координати  .
.

Задача 2.9. Дано три вектори 

 . Знайти розкладання вектора
. Знайти розкладання вектора 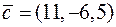 за базисом
за базисом  .
.
Розв’язання.
• Формула розкладання вектора за базисом має вигляд:
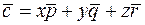 ,
,
де коефіцієнти розкладання  нам буде потрібно знайти.
нам буде потрібно знайти.
Запишемо цю формулу у координатному вигляді.
 ,
,
що приведе до системи рівнянь
 .
.
Розв’яжемо цю систему методом Гауса.
 ;
;
 ;
;
 ;
;  .
.
Значить розкладання має вигляд.
 .
.
Задачі для самостійної роботи
1. Дано координати вектора  :
:  . Знайти координату
. Знайти координату  , якщо відомо, що
, якщо відомо, що  .
.
2. Визначити початок вектора 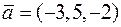 , якщо його кінець співпадає з точкою
, якщо його кінець співпадає з точкою 
3. Дано  та
та  . Знайти модуль суми та різниці цих векторів.
. Знайти модуль суми та різниці цих векторів.
4. Обчислити напрямні косинуси вектора  , якщо
, якщо  та
та  .
.
5. З’ясувати, чи може вектор становити з координатними осями кути  .
.
6. Знайти орт вектора  , де
, де  .
.
7. Вектори  та
та  перпендикулярні та
перпендикулярні та  . Знайти
. Знайти  .
.
8. При яких значеннях  та
та  вектори
вектори  та
та  колінеарні?
колінеарні?
9. Розкласти вектор 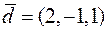 за базисом, що складається з векторів
за базисом, що складається з векторів 
Дата добавления: 2018-11-24; просмотров: 261; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
