Определение точности оценок, получаемых методом наименьших квадратов
Условие задачи 2.4
Навигационный приемник провел измерения псевдодальностей 
 в момент tизм по N навигационным КА (N > 4), где j ‑ порядковый номер измерения, или порядковый номер КА, по которому проведено измерение.
в момент tизм по N навигационным КА (N > 4), где j ‑ порядковый номер измерения, или порядковый номер КА, по которому проведено измерение.
Найти алгоритм обработки N измерений псевдодальностей 
 с целью определения координат xп(tизм), yп(tизм), zп(tизм) навигационного приемника и смещения ΔRп(tизм) (в метрах) его шкалы времени относительно шкалы навигационной системы на момент времени tизм. Задержками распространения сигнала в атмосфере Земли пренебречь.
с целью определения координат xп(tизм), yп(tизм), zп(tизм) навигационного приемника и смещения ΔRп(tизм) (в метрах) его шкалы времени относительно шкалы навигационной системы на момент времени tизм. Задержками распространения сигнала в атмосфере Земли пренебречь.
Условие задачи 2.5
Навигационный приемник в момент 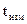 провел измерения псевдодоплеровских смещений частоты несущих колебаний
провел измерения псевдодоплеровских смещений частоты несущих колебаний 
 в момент tизм по N навигационным КА (N > 4), где j ‑ порядковый номер измерения, или порядковый номер КА, по которому проведено измерение.
в момент tизм по N навигационным КА (N > 4), где j ‑ порядковый номер измерения, или порядковый номер КА, по которому проведено измерение.
Найти алгоритм обработки N измерений псевдодоплеровских смещений частоты несущих колебаний 
 с целью определения составляющих
с целью определения составляющих  ,
,  ,
, 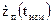 вектора скорости
вектора скорости  навигационного приемника и смещения
навигационного приемника и смещения  частоты его задающего генератора относительно номинального значения. При разработке алгоритма полагать, что координаты xп(tизм), yп(tизм), zп(tизм) навигационного приемника известны (получены в результате предшествующей обработки измерений псевдодальностей).
частоты его задающего генератора относительно номинального значения. При разработке алгоритма полагать, что координаты xп(tизм), yп(tизм), zп(tизм) навигационного приемника известны (получены в результате предшествующей обработки измерений псевдодальностей).
Условие задачи 2.6
Оценить точность определения координат навигационного приемника и смещения его шкалы времени относительно шкалы системы, которые поучены в результате обработки измерений псевдодальностей по всем КА, находящимся в зоне видимости. Вычислить общий, горизонтальный, вертикальный и временной геометрические факторы результатов такой обработки. Полагать, что ошибки измерения псевдодальностей по разным спутникам являются статистически независимыми, точность измерения псевдодальностей одинакова по всем КА, находящихся в зоне видимости и характеризуется среднеквадратической ошибкой  . Задержками распространения сигнала в атмосфере Земли пренебречь.
. Задержками распространения сигнала в атмосфере Земли пренебречь.
|
|
|
Условие задачи 2.7
Оценить точность определения составляющих вектора скорости навигационного приемника и скорости смещения его шкалы времени относительно шкалы системы, которые получены в результате обработки измерений псевдодоплеровских смещений частот несущих колебаний сигналов всех спутников, находящихся в зоне видимости. Вычислить общий, горизонтальный, вертикальный и временной геометрические факторы результатов такой обработки. Полагать, что координаты приемника  ,
,  ,
, 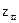 известны, ошибки измерения псевдодоплеровских смещений по разным спутникам статистически независимы, точность измерения псевдодоплеровских смещений одинакова по всем КА, находящихся в зоне видимости и характеризуется среднеквадратической ошибкой
известны, ошибки измерения псевдодоплеровских смещений по разным спутникам статистически независимы, точность измерения псевдодоплеровских смещений одинакова по всем КА, находящихся в зоне видимости и характеризуется среднеквадратической ошибкой  .
.
|
|
|
1.3 УСЛОВИЯ ЗАДАЧ ПО СНОВАМ ТЕОРИИ ГЛОБАЛЬНЫХ НАВИГАЦИОННЫХ СПУТНИКОВЫХ СИСТЕМ
Условие задачи 3.1
Навигационные спутники передают показания своих часов в фазе специального кода, называемого кодом передачи показаний спутниковых часов (КППСЧ). В сигналах открытого доступа систем ГЛОНАСС и GPS период этого кода равен 1мс. Следовательно, с помощью фазы этих кодов можно передать показания спутниковых часов с точностью до целого числа миллисекунд, иными словами фаза КППСЧ переносит только дробную часть миллисекунды в показаниях спутниковых часов.
Каким образом в приемниках ГНСС восстанавливается целое число миллисекунд (разрешается миллисекундная неоднозначность) в показаниях спутниковых часов?
Условие задачи 3.2
Модель радионавигационного приемника в виде совокупности собственных и канальных часов может быть представлена в виде:

Рис. 3.2.1 Модель навигационного приемника
Собственные часы навигационного приемника идут независимо от часов навигационных спутников и часов системы. Показания собственных часов могут периодически корректироваться путем использования оценок смещения этих показаний относительно показаний часов системы.
|
|
|
Ход канальных часов синхронизируется принимаемыми кодами передачи показаний спутниковых часов (КППСЧ), которые в литературе обычно называют дальномерными кодами. Количество канальных часов приемника равно числу одновременно отслеживаемых приемником спутников.
Измерения (оценки) псевдозадержки по j-му спутнику, формируемые в приемнике, равны разности показаний собственных часов приемника  и показаний канальных часов j-го спутника
и показаний канальных часов j-го спутника 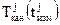 в момент измерения
в момент измерения 
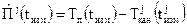 ,
,  . (3.2.1)
. (3.2.1)
Показания канальных часов  на момент измерения
на момент измерения  являются оценками показаний часов j-го спутника
являются оценками показаний часов j-го спутника  на момент времени
на момент времени 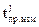 предшествия моменту измерения
предшествия моменту измерения  , т. е.
, т. е.

 . (3.2.2)
. (3.2.2)
где знак ^ над символом обозначает, что этот символ является оценкой, содержащей ошибку оценивания  .
.
Подставляя (3.2.2) в (3.2.1) получаем выражение для измерения (оценки) псевдозадержки
 ,
,  . (3.2.3)
. (3.2.3)
|
|
|
Измерения (оценки) псевдодальности в навигационном приемнике формируются как произведение измеренного значения псевдозадержки на скорость света c
 ,
,  . (3.2.4)
. (3.2.4)
Найти функциональную связь между измерениями (оценками) псевдодальностей 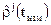 (3.2.4), координатами
(3.2.4), координатами  ,
, 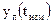 ,
,  точки, которую приемник занимал в момент измерения
точки, которую приемник занимал в момент измерения  и смещением
и смещением  его шкалы времени относительно шкалы системы (смещением показаний его часов относительно показаний часов системы) в тот же момент измерения
его шкалы времени относительно шкалы системы (смещением показаний его часов относительно показаний часов системы) в тот же момент измерения  .
.
Условие задачи 3.3
Построить поверхность положения для измерений псевдодальностей для упрощенного случая радионавигации в двумерном пространстве (в плоскости). Обобщить полученный результат для реального случая радионавигации в трехмерном пространстве
Условие задачи 3.4
Для определения координат приемника на момент измерения  необходимо знать координаты навигационных спутников на моменты предшествия
необходимо знать координаты навигационных спутников на моменты предшествия 
 . Спутники сообщают параметры своих моделей движения, которые определяют траектории движения на длительном интервале времени. Среди бесконечного количества моментов времени на этих интервалах располагаются моменты предшествия
. Спутники сообщают параметры своих моделей движения, которые определяют траектории движения на длительном интервале времени. Среди бесконечного количества моментов времени на этих интервалах располагаются моменты предшествия 
 .
.
Каким образом приемник выделяет эти моменты среди прочих для того, чтобы используя параметры модели движения рассчитать координаты спутников на моменты предшествия 
 ?
?
Условие задачи 3.5
Математическая модель измерений псевдодальностей  имеет вид:
имеет вид:
 ,
,  (3.5.1)
(3.5.1)
где  – расстояние между точками, которые занимал приемник в момент измерения
– расстояние между точками, которые занимал приемник в момент измерения  и j-й спутник в момент предшествия
и j-й спутник в момент предшествия  , который предшествует моменту
, который предшествует моменту  на время распространения сигнала,
на время распространения сигнала,  – смещение показаний часов приемника относительно показаний часов системы в момент
– смещение показаний часов приемника относительно показаний часов системы в момент  .
.
По измерениям псевдодальностей  приемник должен определить гринвичские координаты точки
приемник должен определить гринвичские координаты точки  ,
, 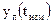 ,
,  , которую он занимал в момент измерения
, которую он занимал в момент измерения  , т. е. координаты в том положении вращающейся гринвичской системы координат, которое она занимает в момент измерения
, т. е. координаты в том положении вращающейся гринвичской системы координат, которое она занимает в момент измерения  . Координаты же точек, которые спутники занимали в моменты предшествия
. Координаты же точек, которые спутники занимали в моменты предшествия  определяются по эфемеридным данным в том положении вращающейся гринвичской системы координат, которые она занимала в эти моменты. Поскольку
определяются по эфемеридным данным в том положении вращающейся гринвичской системы координат, которые она занимала в эти моменты. Поскольку  и
и  разные моменты времени, то положение вращающейся гринвичской системы координат в эти два разных момента времени различается (см. рис. 3.5.1).
разные моменты времени, то положение вращающейся гринвичской системы координат в эти два разных момента времени различается (см. рис. 3.5.1).

Рис. 3.5.1. Положение гринвичской системы координат в моменты измерения и предшествия
Таким образом, расстояние  , входящее в модель псевдодальностей (3.5.1), определяется между точками, координаты которых задаются в разных системах.
, входящее в модель псевдодальностей (3.5.1), определяется между точками, координаты которых задаются в разных системах.
Для обработки измерений псевдодальностей  с целью определения координат приемника
с целью определения координат приемника  ,
, 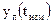 ,
,  в момент измерения
в момент измерения  необходимо дальность
необходимо дальность  , входящую в (3.5.1), выразить как функцию указанных координат. Для этого обычно используется известная формула
, входящую в (3.5.1), выразить как функцию указанных координат. Для этого обычно используется известная формула
 . (3.5.2)
. (3.5.2)
Но поскольку координаты точек, которые занимает приемник в момент измерения  и спутник в момент предшествия
и спутник в момент предшествия  заданы в разных системах, то
заданы в разных системах, то
 , (3.5.3)
, (3.5.3)
Каким образом преодолевается эта проблема в ГНСС?
Условие задачи 3.6
Навигационный приемник в момент 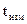 проводит измерения псевдодоплеровских смещений
проводит измерения псевдодоплеровских смещений  частот несущих колебаний спутниковых сигналов
частот несущих колебаний спутниковых сигналов
 ,
,  (3.6.1)
(3.6.1)
по сигналам J ≥ 4 спутников, где  – доплеровское смещение несущей частоты j-го спутника,
– доплеровское смещение несущей частоты j-го спутника,  – постоянный коэффициент преобразования частоты задающего генератора (ЗГ)
– постоянный коэффициент преобразования частоты задающего генератора (ЗГ)  на несущую частоту j-го спутника,
на несущую частоту j-го спутника,  – отклонение частоты
– отклонение частоты  от ее номинального значения
от ее номинального значения  в момент измерения
в момент измерения  . Путем обработки J измерений псевдодоплеровских смещений
. Путем обработки J измерений псевдодоплеровских смещений  приемник находит оценки составляющих своего вектора скорости
приемник находит оценки составляющих своего вектора скорости 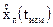 ,
,  ,
,  и оценку
и оценку  отклонения частоты своего задающего генератора (ЗГ) относительно ее номинального значения в момент
отклонения частоты своего задающего генератора (ЗГ) относительно ее номинального значения в момент  .
.
1. Найти функциональную связь между измерениями (оценками) псевдодоплеровских смещений  (3.6.1), составляющими вектора скорости
(3.6.1), составляющими вектора скорости  ,
,  ,
,  навигационного приемника и смещением
навигационного приемника и смещением  частоты его задающего генератора относительно ее номинального значения.
частоты его задающего генератора относительно ее номинального значения.
2. Построить поверхность положения измерений псевдодоплеровских смещений частот несущих колебаний спутниковых сигналов.
Решение задачи 2.4
Составляющими вектора целевых параметров θ в данной задаче являются координаты xп(tизм), yп(tизм), zп(tизм) и смещение ΔRп(tизм) (в метрах) шкалы времени навигационного приемника относительно шкалы системы. Таким образом, вектор оцениваемых параметров θ имеет вид  , а его размерность n равна 4 (n = 4).
, а его размерность n равна 4 (n = 4).
1. Построение алгоритма обработки любых измерений должно начинаться с получения функций связи точных измерений псевдодальностей ρj(tизм) 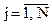 с компонентами оцениваемого вектора θ. Искомая функция, при условии пренебрежения задержками распространения сигнала в атмосфере Земли, выведена в решении задачи 3.2 и имеет вид (см. также учебное пособие [2])
с компонентами оцениваемого вектора θ. Искомая функция, при условии пренебрежения задержками распространения сигнала в атмосфере Земли, выведена в решении задачи 3.2 и имеет вид (см. также учебное пособие [2])

 (2.4.1)
(2.4.1)
где  ‑ моменты времени, предшествующие моменту измерения tизм на время распространения сигнала от j-го КА до навигационного приемника,
‑ моменты времени, предшествующие моменту измерения tизм на время распространения сигнала от j-го КА до навигационного приемника,  ,
,  ,
,  ‑ координаты j-го КА, вычисляемые в навигационном приемнике по эфемеридным данным, сообщаемым каждым КА,
‑ координаты j-го КА, вычисляемые в навигационном приемнике по эфемеридным данным, сообщаемым каждым КА,  ‑ смещение шкалы времени j-го КА относительно шкалы навигационной системы, также вычисляемое в навигационном приемнике по эфемеридным данным, с ‑ скорость света.
‑ смещение шкалы времени j-го КА относительно шкалы навигационной системы, также вычисляемое в навигационном приемнике по эфемеридным данным, с ‑ скорость света.
Далее, для упрощения вида математических выражений обозначение моментов времени, к которым относятся входящие в эти выражения величины, опустим.
2. Навигационные КА могут располагаться под разными углами над горизонтом по отношению к навигационному приемнику. Чем большим является этот угол, тем более точным является измерение псевдодальности. Поэтому в решаемой задаче необходимо использовать сумму взвешенных квадратов невязок V(θ)
 , (2.4.2)
, (2.4.2)
где  ‑ весовые коэффициенты,
‑ весовые коэффициенты,  ‑ дисперсия измерения псевдодальности по j-му КА,
‑ дисперсия измерения псевдодальности по j-му КА,

 (2.4.3)
(2.4.3)
невязка, соответствующая j-му КА,  ‑ измеренные значения псевдодальностей,
‑ измеренные значения псевдодальностей,  .
.
Измеренные значения псевдодальностей  , входящие в (2.4.3), отличаются от их точных значений
, входящие в (2.4.3), отличаются от их точных значений  (2.4.1)
(2.4.1)  на величину ошибок измерений. Дисперсии этих ошибок задаются значениями
на величину ошибок измерений. Дисперсии этих ошибок задаются значениями 
 .
.
Составляющие  , входящие в (2.4.3), являются известными величинами и поэтому их целесообразно объединить с измеренными значениями псевдодальностей
, входящие в (2.4.3), являются известными величинами и поэтому их целесообразно объединить с измеренными значениями псевдодальностей  . Для этого введем в рассмотрение поправленные значения
. Для этого введем в рассмотрение поправленные значения  измеренных псевдодальностей
измеренных псевдодальностей
 .
. 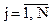 (2.4.4)
(2.4.4)
Тогда выражения (2.4.3) переписываются в следующем более простом виде
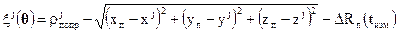 ,
, 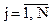 (2.4.5)
(2.4.5)
Для дальнейшего применения выражение (2.4.4) более удобно представить в компактной матричной форме. Для этого введем в рассмотрение N-вектор невязок Ξ
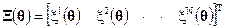 (2.4.6)
(2.4.6)
и (N×N)-матрицу весовых коэффициентов B
 . (2.4.7)
. (2.4.7)
Тогда выражение для взвешенной суммы квадратов невязок (2.4.2) переписывается в следующей компактной матричной форме
 (2.4.8)
(2.4.8)
3. В соответствии с методом наименьших квадратов, в качестве оценки 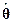 вектора θ принимается то его значение, при котором выполняется условие
вектора θ принимается то его значение, при котором выполняется условие
 (2.4.9)
(2.4.9)
Как известно из математического анализа, оценка  , при которой достигается минимум V(θ), может быть найдена как решение относительно θ следующего нелинейного уравнения
, при которой достигается минимум V(θ), может быть найдена как решение относительно θ следующего нелинейного уравнения
 (2.4.10)
(2.4.10)
Уравнение (2.4.10) является нелинейным и поэтому его решение должно осуществляться итерационным методом.
4. Для решения уравнения (2.4.10) будем использовать упрощенную методику, изложенную в приложении A. С этой целю в скалярной функции 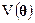 (2.4.8) вектор невязок
(2.4.8) вектор невязок  на каждой s-й итерации будем заменять его линейной аппроксимацией
на каждой s-й итерации будем заменять его линейной аппроксимацией
 , (2.4.11)
, (2.4.11)
где  ‑ вектор невязок, вычисленный в точке предыдущего (s-1)-го приближения
‑ вектор невязок, вычисленный в точке предыдущего (s-1)-го приближения  ,
,  , где H(θ) ‑ (N×4)-матрица первых частных производных от функций (2.4.4) связи точных поправленных измерений
, где H(θ) ‑ (N×4)-матрица первых частных производных от функций (2.4.4) связи точных поправленных измерений  с целевым вектором θ
с целевым вектором θ
 , (2.4.12)
, (2.4.12)
 ,
, 
 (2.4.13)
(2.4.13)
направляющие косинусы единичного вектора, ориентированного из точки расположения j-го КА в точку расположения навигационного приемника, определяемую на каждой итерации,  ‑ расстояние между двумя вышеуказанными точками,
‑ расстояние между двумя вышеуказанными точками,  ‑ матрица (2.4.12), вычисленная для значения ее векторного аргумента
‑ матрица (2.4.12), вычисленная для значения ее векторного аргумента  ,
, 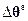 – вектор-столбец поправок
– вектор-столбец поправок
 . (2.4.14)
. (2.4.14)
Для первой итерации в качестве начального приближения к точному решению можно принять оценку вектора  , найденную в предыдущий момент времени. Если же предыдущий момент времени отсутствует, то можно положить
, найденную в предыдущий момент времени. Если же предыдущий момент времени отсутствует, то можно положить  .
.
Заменяем в (2.4.8) вектора невязок  на его линеаризованное выражение (2.4.11), получаем квадратичную аппроксимацию минимизируемой функции
на его линеаризованное выражение (2.4.11), получаем квадратичную аппроксимацию минимизируемой функции  , аргументом которой является 4-вектор поправок
, аргументом которой является 4-вектор поправок 
 (2.4.15)
(2.4.15)
где
 . (2.4.16)
. (2.4.16)
N-вектор  и (N×4)-матрица
и (N×4)-матрица  не зависят от аргумента
не зависят от аргумента  . Благодаря этому, уравнение
. Благодаря этому, уравнение  , решение которого минимизирует функцию
, решение которого минимизирует функцию  (2.4.15), становится линейным.
(2.4.15), становится линейным.
Функция  (2.4.14) является квадратичной формой и, следовательно, является скалярной функцией. Аргументом этой функции является вектор-столбец
(2.4.14) является квадратичной формой и, следовательно, является скалярной функцией. Аргументом этой функции является вектор-столбец  (2.4.16), аргументом которого в свою очередь является вектор поправок
(2.4.16), аргументом которого в свою очередь является вектор поправок  . Это означает, что для вычисления производной
. Это означает, что для вычисления производной  необходимо использовать приведенное в приложении B правило дифференцирования скалярной функции
необходимо использовать приведенное в приложении B правило дифференцирования скалярной функции  от векторного аргумента
от векторного аргумента  (2.4.16), который сам является векторной функцией векторного аргумента
(2.4.16), который сам является векторной функцией векторного аргумента  (сложной скалярной функции векторного аргумента). Дифференцируя (2.4.15) по формулам из приложения B, преобразуем уравнение
(сложной скалярной функции векторного аргумента). Дифференцируя (2.4.15) по формулам из приложения B, преобразуем уравнение  к виду
к виду
 . (2.4.17)
. (2.4.17)
Из (2.4.17) находим оценку поправки 
 , (2.4.18)
, (2.4.18)
Далее по формуле
 (2.4.19)
(2.4.19)
вычисляем следующее приближение к точному решению  . Заменяя в (2.4.18)
. Заменяя в (2.4.18)  на оценку
на оценку  , вычисляем поправку
, вычисляем поправку  на (s+1)-й итерации и далее по формуле аналогичной (2.4.19), вычисляем приближение
на (s+1)-й итерации и далее по формуле аналогичной (2.4.19), вычисляем приближение  к точному решению на (s+1)-й итерации. Продолжаем такие итерационные вычисления до тех пор, пока все элементы вектора поправок к предыдущему решению на очередной итерации станут по модулю менее 1 м.
к точному решению на (s+1)-й итерации. Продолжаем такие итерационные вычисления до тех пор, пока все элементы вектора поправок к предыдущему решению на очередной итерации станут по модулю менее 1 м.
Решение задачи 2.5
Для удобства решения задачи введем в рассмотрение оцениваемый вектор
 , (2.5.1)
, (2.5.1)
компонентами которого являются составляющие  ,
,  ,
,  вектора скорости
вектора скорости
 (2.5.2)
(2.5.2)
навигационного приемника и смещение  частоты его задающего генератора относительно номинального значения в момент измерения
частоты его задающего генератора относительно номинального значения в момент измерения  . Для обработки измерений псевдодоплеровских смещений
. Для обработки измерений псевдодоплеровских смещений 
 частот несущих колебаний спутниковых сигналов с целью определения 4-х компонент вектора
частот несущих колебаний спутниковых сигналов с целью определения 4-х компонент вектора  (2.5.1), необходимо найти функциональную связь этих компонент с результатами измерений. Такая связь, найденная в решении задачи 3.6, имеет вид
(2.5.1), необходимо найти функциональную связь этих компонент с результатами измерений. Такая связь, найденная в решении задачи 3.6, имеет вид

 (2.5.3)
(2.5.3)
где  ‑ номинальная длина волны несущего колебания j-го КА,
‑ номинальная длина волны несущего колебания j-го КА,
 ,
,  ,
,  (2.5.4)
(2.5.4)
направляющие косинусы единичного вектора, ориентированного из точки расположения j-го КА в момент  , который предшествует моменту измерения
, который предшествует моменту измерения  на время распространения сигнала, в точку расположения навигационного приемника в момент измерения
на время распространения сигнала, в точку расположения навигационного приемника в момент измерения  ,
, 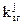 ‑ постоянный коэффициент преобразования частоты задающего генератора (ЗГ)
‑ постоянный коэффициент преобразования частоты задающего генератора (ЗГ)  на несущую частоту j-го спутника,
на несущую частоту j-го спутника,  ,
,  ,
, 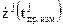 ‑ составляющие вектора скорости j-го КА в момент
‑ составляющие вектора скорости j-го КА в момент 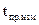 . Далее, для упрощения вида математических выражений обозначение моментов времени, к которым относятся входящие в эти выражения величины, опустим.
. Далее, для упрощения вида математических выражений обозначение моментов времени, к которым относятся входящие в эти выражения величины, опустим.
Из (2.5.3) получаем следующую, в общем случае избыточную систему из J (J – общее количество КА, одновременно отслеживаемых приемником) уравнений относительно переменных  ,
,  ,
,  ,
,  :
:

 , (2.5.5)
, (2.5.5)
где  – номинальная длина волны сигнала задающего генератора приемника,
– номинальная длина волны сигнала задающего генератора приемника,  ‑ измеренное (т. е. содержащее погрешности измерений) значение псевдодоплеровского смещения по j-му КА.
‑ измеренное (т. е. содержащее погрешности измерений) значение псевдодоплеровского смещения по j-му КА.
Нетрудно видеть, что система (2.5.5) является линейной. Поэтому ее решение может быть найдено без использования итерационного процесса, т. е. в аналитической форме. Для записи такого решения введем в рассмотрение следующие векторно-матричные обозначения:
 ; (2.5.6)
; (2.5.6)
 , (2.5.7)
, (2.5.7)
где составляющие  ,
,  , вектора
, вектора  равны правым частям уравнений системы (2.5.5):
равны правым частям уравнений системы (2.5.5):
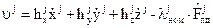
 . (2.5.8)
. (2.5.8)
Тогда система линейных уравнений (2.5.5) переписывается в следующем матричном виде
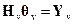 . (2.5.9)
. (2.5.9)
При измерении псевдодоплеровских смещений  относительно 4-х КА оценки
относительно 4-х КА оценки  ,
,  ,
,  ,
,  компонент вектора
компонент вектора  (2.5.1) решение системы (2.5.9) записывается в виде:
(2.5.1) решение системы (2.5.9) записывается в виде:
 . (2.5.10)
. (2.5.10)
Однако на практике число КА, по которым ведутся измерения, обычно больше 4-х. В этом случае используется решение наименьших квадратов, рассмотренное в приложении А.
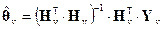 . (2.5.11)
. (2.5.11)
Измерения, полученные по разным КА, могут при обработке учитываться с разными весами. В этом случае решение системы (2.5.9) записывается в виде:
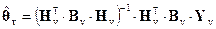 , (2.5.16)
, (2.5.16)
где  – весовая матрица, которая обычно вычисляется как матрица, обратная к ковариационной матрице
– весовая матрица, которая обычно вычисляется как матрица, обратная к ковариационной матрице  ошибок компонент вектора
ошибок компонент вектора  (2.5.7).
(2.5.7).
Решение задачи 2.6
Оценку точности определения координат  ,
,  ,
,  навигационного приемника и смещения
навигационного приемника и смещения  его шкалы времени относительно шкалы системы по измерениям псевдодальностей
его шкалы времени относительно шкалы системы по измерениям псевдодальностей  будем проводить, используя методику, изложенную в приложении C.
будем проводить, используя методику, изложенную в приложении C.
В соответствии с условием задачи оцениваемый вектор
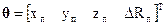 (2.6.1)
(2.6.1)
имеет 4 компоненты. Функции связи компонент оцениваемого вектора с измерениями псевдодальностей  при условии пренебрежения задержками распространения сигнала в атмосфере Земли, выведены в решении задачи 3.2 и имеют вид (см. также учебное пособие [2])
при условии пренебрежения задержками распространения сигнала в атмосфере Земли, выведены в решении задачи 3.2 и имеют вид (см. также учебное пособие [2])

 (2.6.2)
(2.6.2)
где  ,
,  ,
,  ‑ координаты j-го КА, вычисляемые в навигационном приемнике по эфемеридным данным,
‑ координаты j-го КА, вычисляемые в навигационном приемнике по эфемеридным данным,  ‑ смещение шкалы времени j-го КА относительно шкалы навигационной системы, также вычисляемое в навигационном приемнике по эфемеридным данным, с ‑ скорость света, N – число КА, по которым осуществляются измерения псевдодальностей (N ≥ 4).
‑ смещение шкалы времени j-го КА относительно шкалы навигационной системы, также вычисляемое в навигационном приемнике по эфемеридным данным, с ‑ скорость света, N – число КА, по которым осуществляются измерения псевдодальностей (N ≥ 4).
Из (2.6.2) видим, что функции, связи компонент  ,
,  ,
,  ,
,  оцениваемого вектора
оцениваемого вектора  (2.6.1) с измерениями псевдодальностей
(2.6.1) с измерениями псевдодальностей  являются нелинейными. Следовательно, для определения точности компонент векторной оценки
являются нелинейными. Следовательно, для определения точности компонент векторной оценки
 , (2.6.3)
, (2.6.3)
полученной путем обработки измерений псевдодальностей методом наименьших квадратов необходимо использовать приближенную методику, изложенную в приложении C. В соответствии с этой методикой ковариационная матрица  ошибок векторной оценки
ошибок векторной оценки  (2.6.3), определяющая точность оценивания этих компонент, может быть вычислена по формуле (C.9) из приложения C
(2.6.3), определяющая точность оценивания этих компонент, может быть вычислена по формуле (C.9) из приложения C
 (2.6.4)
(2.6.4)
где  ‑ матрица
‑ матрица  (A.23), вычисленная в точке наименьших квадратов
(A.23), вычисленная в точке наименьших квадратов  . Для функций связи компонент оцениваемого вектора с измерениями псевдодальностей
. Для функций связи компонент оцениваемого вектора с измерениями псевдодальностей  вида (2.6.2) матрица
вида (2.6.2) матрица  в (2.6.4) имеет вид
в (2.6.4) имеет вид
 , (2.6.5)
, (2.6.5)
где
 ,
,  ,
,  ,
,  (2.6.6)
(2.6.6)
направляющие косинусы единичного вектора, ориентированного из точки расположения j-го КА в точку с координатами  ,
,  ,
,  , которые являются оценками координат навигационного приемника, полученными методом наименьших квадратов (см. приложение A и решение задачи 2.4),
, которые являются оценками координат навигационного приемника, полученными методом наименьших квадратов (см. приложение A и решение задачи 2.4),  ,
,  ,
,  ‑ координаты j-го КА, вычисляемые в навигационном приемнике по эфемеридным данным,
‑ координаты j-го КА, вычисляемые в навигационном приемнике по эфемеридным данным,
 (2.6.7)
(2.6.7)
расстояние между j-м КА и точкой с координатами  ,
,  ,
,  ,
,  ‑ (N×N)-матрица обратная к ковариационной матрице
‑ (N×N)-матрица обратная к ковариационной матрице  ошибок измерений псевдодальностей. В связи с тем, что по условию задачи ошибки измерения псевдодальностей по разным КА полагаются статистически независимыми и характеризуются одинаковыми среднеквадратическими ошибками
ошибок измерений псевдодальностей. В связи с тем, что по условию задачи ошибки измерения псевдодальностей по разным КА полагаются статистически независимыми и характеризуются одинаковыми среднеквадратическими ошибками  , (N×N)-матрица
, (N×N)-матрица  имеет вид
имеет вид
 , (2.6.8)
, (2.6.8)
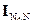 ‑ единичная (N×N)-матрица.
‑ единичная (N×N)-матрица.
Направляющие косинусы 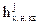 ,
,  ,
,  строк матрицы
строк матрицы  (2.6.5) вычислялись в гринвичской системе координат. Поэтому ковариационная матрица
(2.6.5) вычислялись в гринвичской системе координат. Поэтому ковариационная матрица 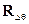 , вычисленная с помощью (2.6.4), будет характеризовать ошибки местоположения приемника вдоль осей гринвичской системы координат. Но в реальной жизни потребителя навигационной информации обычно интересуют характеристики ошибок местоположения в местной горизонтальной плоскости и по вертикали, т.е. в локальной (топоцентрической) системе координат. Для вычисления ковариационной матрицы ошибок местоположения вдоль осей местной системы все направляющие косинусы, входящие в матрицу
, вычисленная с помощью (2.6.4), будет характеризовать ошибки местоположения приемника вдоль осей гринвичской системы координат. Но в реальной жизни потребителя навигационной информации обычно интересуют характеристики ошибок местоположения в местной горизонтальной плоскости и по вертикали, т.е. в локальной (топоцентрической) системе координат. Для вычисления ковариационной матрицы ошибок местоположения вдоль осей местной системы все направляющие косинусы, входящие в матрицу  (2.6.5), необходимо пересчитать в местную систему координат. Для каждого j-го единичного вектора
(2.6.5), необходимо пересчитать в местную систему координат. Для каждого j-го единичного вектора  , образуемого направляющими косинусами
, образуемого направляющими косинусами  ,
,  ,
,  такой пересчет может быть осуществлен по формуле
такой пересчет может быть осуществлен по формуле

 (2.6.9)
(2.6.9)
где 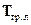 - матрица перехода из гринвичской в локальную систему координат. Для простейшей сферической модели Земли такая матрица задается выражением
- матрица перехода из гринвичской в локальную систему координат. Для простейшей сферической модели Земли такая матрица задается выражением
 (2.6.10)
(2.6.10)
где λ и φ географические широта и долгота точки расположения приемника на поверхности Земли.
Подставляя (2.6.8) в (2.6.4) получаем:
 (2.6.11)
(2.6.11)
Элементы, стоящие на главной диагонали матрицы 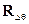 (2.6.11), являются дисперсиями ошибок оценок
(2.6.11), являются дисперсиями ошибок оценок  ,
,  ,
,  ,
,  , которые являются компонентами вектора наименьших квадратов
, которые являются компонентами вектора наименьших квадратов  . Благодаря тому, что направляющие косинусы, образующие первые три элемента каждой строки матрицы
. Благодаря тому, что направляющие косинусы, образующие первые три элемента каждой строки матрицы  (2.6.5) были пересчитаны в локальную систему координат, первые два диагональных элемента матрицы
(2.6.5) были пересчитаны в локальную систему координат, первые два диагональных элемента матрицы  (2.6.11) будут дисперсиями ошибок местоопределения в горизонтальной плоскости, т. е. дисперсиями ошибок определения первых двух компонент
(2.6.11) будут дисперсиями ошибок местоопределения в горизонтальной плоскости, т. е. дисперсиями ошибок определения первых двух компонент  ,
, 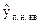 векторной оценки
векторной оценки  (2.6.3). Третий диагональный элемент матрицы
(2.6.3). Третий диагональный элемент матрицы 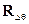 (2.6.11) будет дисперсией ошибки местоопределения по местной вертикали, т. е. дисперсией ошибки определения третьей компоненты
(2.6.11) будет дисперсией ошибки местоопределения по местной вертикали, т. е. дисперсией ошибки определения третьей компоненты  векторной оценки
векторной оценки  (2.6.3). Четвертый диагональный элемент матрицы
(2.6.3). Четвертый диагональный элемент матрицы 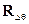 (2.6.11) будет, как и ранее, дисперсией временной ошибки, т. е. дисперсией ошибки определения четвертой компоненты
(2.6.11) будет, как и ранее, дисперсией временной ошибки, т. е. дисперсией ошибки определения четвертой компоненты  векторной оценки
векторной оценки  (2.6.3). Иными словами четвертый диагональный элемент матрицы
(2.6.3). Иными словами четвертый диагональный элемент матрицы 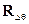 (2.6.11) будет дисперсией ошибки определения смещения показаний собственных часов приемника относительно часов системы.
(2.6.11) будет дисперсией ошибки определения смещения показаний собственных часов приемника относительно часов системы.
Суммируя эти четыре дисперсии и извлекая из суммы квадратный корень, мы получим значение суммарной среднеквадратической ошибки оценки всех элементов векторной оценки  (2.6.3):
(2.6.3):
 , (2.6.12)
, (2.6.12)
где операция tr означает вычисления следа матрицы 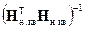 , т.е. суммы ее элементов, стоящих на главной диагонали.
, т.е. суммы ее элементов, стоящих на главной диагонали.
Если мы хотим оценить влияние на точность определения оценки наименьших квадратов  только геометрии расположения спутников относительно приемника, значение
только геометрии расположения спутников относительно приемника, значение  (2.6.12) необходимо разделить на
(2.6.12) необходимо разделить на  . В результате получаем выражение для вычисления общего геометрического фактора
. В результате получаем выражение для вычисления общего геометрического фактора  :
:
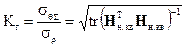 (2.6.13)
(2.6.13)
Типичное значение  при полностью развернутой спутниковой группировке равно ~2.3 [3].
при полностью развернутой спутниковой группировке равно ~2.3 [3].
Наряду с  на практике используются так же более частные геометрические факторы:
на практике используются так же более частные геометрические факторы:
1. Геометрический фактор местоположения 
 (2.6.14)
(2.6.14)
где операция  означает суммирование только первых трех элементов главной диагонали матрицы
означает суммирование только первых трех элементов главной диагонали матрицы  . Типичное значение
. Типичное значение  при полностью развернутой спутниковой группировке равно ~2 [3].
при полностью развернутой спутниковой группировке равно ~2 [3].
2. Горизонтальный геометрический фактор 
 (2.6.15)
(2.6.15)
где операция  означает суммирование только первых двух элементов главной диагонали матрицы
означает суммирование только первых двух элементов главной диагонали матрицы  . Типичное значение
. Типичное значение  при полностью развернутой спутниковой группировке равно ~1.2 [3].
при полностью развернутой спутниковой группировке равно ~1.2 [3].
3. Вертикальный геометрический фактор 
 (2.6.16)
(2.6.16)
где операция  означает выделение только третьего элемента главной диагонали матрицы
означает выделение только третьего элемента главной диагонали матрицы  . Типичное значение
. Типичное значение  при полностью развернутой спутниковой группировке равно ~1.7 [3].
при полностью развернутой спутниковой группировке равно ~1.7 [3].
4. Временной геометрический фактор 
 (2.6.17)
(2.6.17)
где операция  означает выделение только четвертого элемента главной диагонали матрицы
означает выделение только четвертого элемента главной диагонали матрицы  . Типичное значение
. Типичное значение  при полностью развернутой спутниковой группировке равно ~1 [3].
при полностью развернутой спутниковой группировке равно ~1 [3].
Формулы (2.6.14)-(2.6.17) используются на практике для вычисления различных видов геометрического фактора местоопределения обычно по данным альманаха навигационной системы.
Решение задачи 1.2.7
Оценку точности определения составляющих  ,
,  ,
,  вектора скорости навигационного приемника и смещения
вектора скорости навигационного приемника и смещения  частоты его задающего генератора по измерениям псевдодоплеровских смещений
частоты его задающего генератора по измерениям псевдодоплеровских смещений 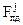 частот несущих колебаний спутниковых сигналов будем проводить, используя методику, изложенную в приложении C.
частот несущих колебаний спутниковых сигналов будем проводить, используя методику, изложенную в приложении C.
В соответствии с условием задачи оцениваемый вектор
 (2.7.1)
(2.7.1)
имеет 4 компоненты. Функции связи компонент оцениваемого вектора с измерениями  псевдододоплеровских смещений частот несущих колебаний спутниковых сигналов выведены в решении задачи 3.6 и имеют вид
псевдододоплеровских смещений частот несущих колебаний спутниковых сигналов выведены в решении задачи 3.6 и имеют вид

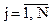 (2.7.2)
(2.7.2)
где  ‑ номинальная длина волны несущего колебания j-го КА,
‑ номинальная длина волны несущего колебания j-го КА,
 ,
,  ,
,  (2.7.3)
(2.7.3)
направляющие косинусы единичного вектора, ориентированного из точки расположения j-го КА в точку расположения навигационного приемника,  ‑ постоянный коэффициент преобразования частоты
‑ постоянный коэффициент преобразования частоты  задающего генератора (ЗГ) на несущую частоту j-го спутника,
задающего генератора (ЗГ) на несущую частоту j-го спутника, 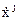 ,
,  ,
,  ‑ составляющие вектора скорости j-го КА, N – число КА, по которым осуществляются измерения псевдодальностей (N ≥ 4)
‑ составляющие вектора скорости j-го КА, N – число КА, по которым осуществляются измерения псевдодальностей (N ≥ 4)
Из (2.7.2) видим, что функции, связи компонент  ,
,  ,
,  ,
,  оцениваемого вектора
оцениваемого вектора  (2.7.1)с измерениями псевдодоплеровских смещений
(2.7.1)с измерениями псевдодоплеровских смещений  частот несущих колебаний спутниковых сигналов являются линейными. Следовательно, для определения точности компонент векторной оценки
частот несущих колебаний спутниковых сигналов являются линейными. Следовательно, для определения точности компонент векторной оценки
 , (2.7.3)
, (2.7.3)
полученной путем обработки измерений псевдодоплеровских смещений частот несущих колебаний спутниковых сигналов методом наименьших квадратов необходимо использовать точную методику, изложенную в приложении C. В соответствии с этой методикой ковариационная матрица 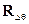 ошибок векторной оценки
ошибок векторной оценки  (2.7.3) методом наименьших квадратов, определяющая точность оценивания этих компонент, может быть вычислена по формуле (C.4) из приложения C
(2.7.3) методом наименьших квадратов, определяющая точность оценивания этих компонент, может быть вычислена по формуле (C.4) из приложения C
 (2.7.4)
(2.7.4)
Для функций связи компонент оцениваемого вектора с измерениями псевдодоплеровских смещений  частот несущих колебаний спутниковых сигналов вида (2.7.2) матрица
частот несущих колебаний спутниковых сигналов вида (2.7.2) матрица  , входящая в (2.7.4) имеет вид
, входящая в (2.7.4) имеет вид
 , (2.7.5)
, (2.7.5)
где
 ,
,  ,
,  ,
,  (2.7.6)
(2.7.6)
направляющие косинусы единичного вектора, ориентированного из точки расположения j-го КА в точку расположения навигационного приемника, координаты которого 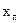 ,
,  ,
,  по условию задачи полагаются известными,
по условию задачи полагаются известными,  ,
,  ,
,  ‑ координаты j-го КА, вычисляемые в навигационном приемнике по эфемеридным данным,
‑ координаты j-го КА, вычисляемые в навигационном приемнике по эфемеридным данным,  ‑ расстояние между j-м КА и навигационным приемником,
‑ расстояние между j-м КА и навигационным приемником,  ‑ (N×N)-матрица обратная к ковариационной матрице
‑ (N×N)-матрица обратная к ковариационной матрице  ошибок измерений псевдодоплеровских смещений частот несущих колебаний спутниковых сигналов. В связи с тем, что по условию задачи ошибки измерения псевдододоплеровских смещений частот несущих колебаний спутниковых сигналов по разным КА полагаются статистически независимыми и характеризуются одинаковыми среднеквадратическими ошибками
ошибок измерений псевдодоплеровских смещений частот несущих колебаний спутниковых сигналов. В связи с тем, что по условию задачи ошибки измерения псевдододоплеровских смещений частот несущих колебаний спутниковых сигналов по разным КА полагаются статистически независимыми и характеризуются одинаковыми среднеквадратическими ошибками  , (N×N)-матрица
, (N×N)-матрица  имеет вид
имеет вид
 , (2.7.7)
, (2.7.7)
 ‑ единичная (N×N)-матрица.
‑ единичная (N×N)-матрица.
Направляющие косинусы  ,
,  ,
,  строк матрицы
строк матрицы 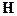 (2.7.5) вычислялись в гринвичской системе координат. Поэтому ковариационная матрица
(2.7.5) вычислялись в гринвичской системе координат. Поэтому ковариационная матрица  , вычисленная с помощью (2.7.4), будет характеризовать ошибки местоположения приемника вдоль осей гринвичской системы координат. Но в реальной жизни потребителя навигационной информации обычно интересуют характеристики ошибок местоположения в местной горизонтальной плоскости и по вертикали, т.е. в локальной (топоцентрической) системе координат. Для вычисления ковариационной матрицы ошибок местоположения вдоль осей местной системы все направляющие косинусы, входящие в матрицу
, вычисленная с помощью (2.7.4), будет характеризовать ошибки местоположения приемника вдоль осей гринвичской системы координат. Но в реальной жизни потребителя навигационной информации обычно интересуют характеристики ошибок местоположения в местной горизонтальной плоскости и по вертикали, т.е. в локальной (топоцентрической) системе координат. Для вычисления ковариационной матрицы ошибок местоположения вдоль осей местной системы все направляющие косинусы, входящие в матрицу  (2.7.5), необходимо пересчитать в местную систему координат. Для каждого j-го единичного вектора
(2.7.5), необходимо пересчитать в местную систему координат. Для каждого j-го единичного вектора  , образуемого направляющими косинусами
, образуемого направляющими косинусами  ,
,  ,
,  такой пересчет может быть осуществлен по формуле
такой пересчет может быть осуществлен по формуле

 (2.7.8)
(2.7.8)
где  - матрица перехода из гринвичской в локальную систему координат. Для простейшей сферической модели Земли такая матрица задается выражением
- матрица перехода из гринвичской в локальную систему координат. Для простейшей сферической модели Земли такая матрица задается выражением
 (2.7.9)
(2.7.9)
где λ и φ географические широта и долгота точки расположения приемника на поверхности Земли.
Подставляя (2.7.7) в (2.7.4) получаем:
 (2.7.10)
(2.7.10)
Элементы, стоящие на главной диагонали матрицы  (2.7.10), являются дисперсиями ошибок оценок
(2.7.10), являются дисперсиями ошибок оценок  ,
,  ,
,  ,
,  , которые являются компонентами вектора наименьших квадратов
, которые являются компонентами вектора наименьших квадратов  (2.7.3). Благодаря тому, что направляющие косинусы, образующие первые три элемента каждой строки матрицы
(2.7.3). Благодаря тому, что направляющие косинусы, образующие первые три элемента каждой строки матрицы 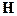 (2.7.5) были пересчитаны в локальную систему координат, первые два диагональных элемента матрицы
(2.7.5) были пересчитаны в локальную систему координат, первые два диагональных элемента матрицы  (2.7.10) будут дисперсиями ошибок местоопределения составляющих вектора скорости навигационного приемника в горизонтальной плоскости, т. е. дисперсиями ошибок определения первых двух компонент
(2.7.10) будут дисперсиями ошибок местоопределения составляющих вектора скорости навигационного приемника в горизонтальной плоскости, т. е. дисперсиями ошибок определения первых двух компонент  ,
,  векторной оценки
векторной оценки  (2.7.3). Третий диагональный элемент матрицы
(2.7.3). Третий диагональный элемент матрицы  (2.7.10) будет дисперсией ошибки вертикальной составляющей вектора скорости навигационного приемника, т. е. дисперсией ошибки определения третьей компоненты
(2.7.10) будет дисперсией ошибки вертикальной составляющей вектора скорости навигационного приемника, т. е. дисперсией ошибки определения третьей компоненты  векторной оценки
векторной оценки  (2.7.3). Четвертый диагональный элемент матрицы
(2.7.3). Четвертый диагональный элемент матрицы  (2.7.10) будет дисперсией ошибки определения смещения частоты задающего генератора навигационного приемника, т. е. дисперсией ошибки определения четвертой компоненты
(2.7.10) будет дисперсией ошибки определения смещения частоты задающего генератора навигационного приемника, т. е. дисперсией ошибки определения четвертой компоненты 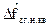 векторной оценки
векторной оценки  (2.7.3).
(2.7.3).
Суммируя эти четыре дисперсии и извлекая из суммы квадратный корень, мы получим значение суммарной среднеквадратической ошибки оценивания всех элементов векторной оценки  (2.7.3):
(2.7.3):
 , (2.7.11)
, (2.7.11)
где операция tr означает вычисления следа матрицы  , т.е. суммы ее элементов, стоящих на главной диагонали.
, т.е. суммы ее элементов, стоящих на главной диагонали.
Если мы хотим оценить влияние на точность определения скоростной оценки наименьших квадратов  только геометрии расположения спутников относительно приемника, значение
только геометрии расположения спутников относительно приемника, значение  (2.7.11) необходимо разделить на
(2.7.11) необходимо разделить на  . В результате получаем выражение для вычисления общего геометрического фактора
. В результате получаем выражение для вычисления общего геометрического фактора  :
:
 (2.7.12)
(2.7.12)
Типичное значение  при полностью развернутой спутниковой группировке равно ~2.3 [3].
при полностью развернутой спутниковой группировке равно ~2.3 [3].
Наряду с  на практике используются так же более частные скоростные геометрические факторы:
на практике используются так же более частные скоростные геометрические факторы:
5. Скоростной геометрический фактор 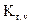
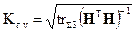 (2.7.13)
(2.7.13)
где операция  означает суммирование только первых трех элементов главной диагонали матрицы
означает суммирование только первых трех элементов главной диагонали матрицы  . Типичное значение скоростного геометрического фактора
. Типичное значение скоростного геометрического фактора  при полностью развернутой спутниковой группировке равно ~2 [3].
при полностью развернутой спутниковой группировке равно ~2 [3].
6. Горизонтальный скоростной геометрический фактор 
 (2.7.14)
(2.7.14)
где операция  означает суммирование только первых двух элементов главной диагонали матрицы
означает суммирование только первых двух элементов главной диагонали матрицы  . Типичное значение горизонтального скоростного геометрического фактора
. Типичное значение горизонтального скоростного геометрического фактора  при полностью развернутой спутниковой группировке равно ~1.2 [3].
при полностью развернутой спутниковой группировке равно ~1.2 [3].
7. Вертикальный геометрический фактор 
 (2.7.15)
(2.7.15)
где операция  означает выделение только третьего элемента главной диагонали матрицы
означает выделение только третьего элемента главной диагонали матрицы  . Типичное значение вертикального геометрического фактора
. Типичное значение вертикального геометрического фактора  при полностью развернутой спутниковой группировке равно ~1.7 [3].
при полностью развернутой спутниковой группировке равно ~1.7 [3].
8. Частотный геометрический фактор 
 (2.7.16)
(2.7.16)
где операция  означает выделение только четвертого элемента главной диагонали матрицы
означает выделение только четвертого элемента главной диагонали матрицы  . Типичное значение частотного геометрического фактора
. Типичное значение частотного геометрического фактора  при полностью развернутой спутниковой группировке равно ~1 [3].
при полностью развернутой спутниковой группировке равно ~1 [3].
Формулы (2.7.13)-(2.7.16) используются на практике для вычисления различных видов скоростного геометрического фактора обычно по данным альманаха навигационной системы.
2.3 РЕШЕНИЯ ЗАДАЧ ПО ОСНОВАМ ТЕОРИИ ГЛОБАЛЬНЫХ НАВИГАЦИОННЫХ СПУТНИКОВЫХ СИСТЕМ
Решение задачи 3.1
В навигационных сообщениях ГНСС помимо параметров моделей движения КА и параметров полиномиальных моделей расхождения показаний часов спутника и системы передаются сигналы меток времени и их оцифровки. Сигнал метки времени представляет собою некоторую фиксированную последовательность импульсов конечной длины (300 мс в ГЛОНАСС и 160 мс в GPS), в которой момент переднего либо заднего фронта одного из импульсов сигнала метки времени называют меткой времени. Таким образом, метка времени это момент, обозначаемый определенным фронтом определенного импульса в структуре сигнала метки времени. Оцифровка метки времени, передаваемая в навигационном сообщении, является данными, которые позволяют вычислить в навигационном приемнике показания часов навигационного спутника в момент излучения с его борта фронта импульса, обозначающего метку времени. Далее, будем оцифровки метки времени j-го спутника обозначать символом  и для простоты полагать, что значение
и для простоты полагать, что значение  равно непосредственно показаниям часов навигационного спутника в момент излучения с его борта фронта импульса, обозначающего метку времени. Все вышеперечисленные понятия показаны на рис. 3.1.1
равно непосредственно показаниям часов навигационного спутника в момент излучения с его борта фронта импульса, обозначающего метку времени. Все вышеперечисленные понятия показаны на рис. 3.1.1

Рис. 3.1.1 Положение меток времени на оси физического времени на спутнике и в приемнике
На рис. 3.1.1а большой вертикальной стрелкой обозначена метка (т. е. момент) времени, а символ  , указанный над нею, обозначает оцифровку этой метки времени, т. е. то, что показывали спутниковые часы в момент излучения с борта спутника фронта импульса, обозначающего метку времени. Далее на рис. 3.1.1а малыми стрелками показаны начала/концы периодов КППСЧ, излучаемых с борта навигационного спутника. На интервалах физического времени между стрелками на рис. 3.1.1а показания часов спутника прирастают на 1 мс и на этих же интервалах располагаются периоды излучаемого КППСЧ.
, указанный над нею, обозначает оцифровку этой метки времени, т. е. то, что показывали спутниковые часы в момент излучения с борта спутника фронта импульса, обозначающего метку времени. Далее на рис. 3.1.1а малыми стрелками показаны начала/концы периодов КППСЧ, излучаемых с борта навигационного спутника. На интервалах физического времени между стрелками на рис. 3.1.1а показания часов спутника прирастают на 1 мс и на этих же интервалах располагаются периоды излучаемого КППСЧ.
На рис. 3.1.1б черточками, направленными вниз, обозначены некоторые регулярные моменты времени на шкале времени приемника, т. е. в эти моменты физического времени показания часов навигационного приемника прирастают на одинаковую величину, например равную 1 мс. При этом совсем не обязательно предполагать, что известны конкретные значения показаний часов приемника в эти моменты. В момент времени, помеченный на рис. 3.1.1б символом  , в навигационном приемнике осуществляется оценивание (измерение) дольной фазы
, в навигационном приемнике осуществляется оценивание (измерение) дольной фазы  принимаемого КППСЧ, которое равно доле периода принимаемого КППСЧ в момент
принимаемого КППСЧ, которое равно доле периода принимаемого КППСЧ в момент  . Значение
. Значение  , выраженное в циклах, является той долей периода принимаемого КППСЧ, которая наблюдается в навигационном приемнике момент
, выраженное в циклах, является той долей периода принимаемого КППСЧ, которая наблюдается в навигационном приемнике момент  .
.
 (3.1.1)
(3.1.1)
Из рис. 3.1.1 видим, что измерение  , формируемое в момент
, формируемое в момент  , является оценкой дробной части миллисекунды
, является оценкой дробной части миллисекунды  в показаниях спутниковых часов в момент предшествия
в показаниях спутниковых часов в момент предшествия  , который предшествует моменту измерения
, который предшествует моменту измерения  на время распространения сигнала. Полные показания
на время распространения сигнала. Полные показания  спутниковых часов в момент предшествия
спутниковых часов в момент предшествия  очевидно равны
очевидно равны
 (3.1.2)
(3.1.2)
где  – оцифровка метки времени, выраженная в мс,
– оцифровка метки времени, выраженная в мс,  – целое число периодов КППСЧ, лежащих на интервале времени от метки времени до момента предшествия
– целое число периодов КППСЧ, лежащих на интервале времени от метки времени до момента предшествия  ,
,  – фаза излучаемого КППСЧ в момент
– фаза излучаемого КППСЧ в момент  ,
,  – множитель для перевода миллисекунд в секунды.
– множитель для перевода миллисекунд в секунды.
Все величины, входящие в (3.1.2) могут быть измерены либо выделены из принимаемого сигнала. Из рис. 3.1.1б видим, что в навигационном приемнике может быть сформирована оценка показаний  часов навигационного спутника путем вычислений по формуле:
часов навигационного спутника путем вычислений по формуле:
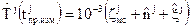 (3.1.3)
(3.1.3)
где  – оцифровка метки времени, выделенная из принимаемого сигнала и выраженная в мс,
– оцифровка метки времени, выделенная из принимаемого сигнала и выраженная в мс,  – целое число периодов КППСЧ, лежащих на интервале времени от метки времени в принимаемом сигнале до момента измерения
– целое число периодов КППСЧ, лежащих на интервале времени от метки времени в принимаемом сигнале до момента измерения  ,
,  – оценка фазы принимаемого КППСЧ, формируемая в навигационном приемнике в момент
– оценка фазы принимаемого КППСЧ, формируемая в навигационном приемнике в момент  ,
,  – множитель для перевода миллисекунд в секунды.
– множитель для перевода миллисекунд в секунды.
Подводя итог рассмотрению, приведенному выше, делаем вывод о том, что восстановление целого число миллисекунд (разрешение миллисекундной неоднозначности) в показаниях спутниковых часов осуществляется в навигационном приемнике путем:
· Использования оцифровок  меток времени, передаваемых в составе навигационного сообщения
меток времени, передаваемых в составе навигационного сообщения
· Счета целого количества периодов КППСЧ  в принимаемом сигнале, лежащих на интервале времени от момента появления в этом сигнале метки времени до момента
в принимаемом сигнале, лежащих на интервале времени от момента появления в этом сигнале метки времени до момента 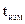 формирования оценки
формирования оценки  (измерения) фазы принимаемого КППСЧ.
(измерения) фазы принимаемого КППСЧ.
Решение задачи 3.2
Для произвольного момента физического времени t (т. е. не только для момента времени проведения измерения  ) выражение (3.2.1) для измерений псевдозадержки можно переписать следующим образом:
) выражение (3.2.1) для измерений псевдозадержки можно переписать следующим образом:
 ,
,  , (3.2.5)
, (3.2.5)
где символ  обозначает момент предшествия текущему моменту физического времени t.
обозначает момент предшествия текущему моменту физического времени t.
На любой момент физического времени t можно ввести понятия смещений показаний часов спутника  и собственных часов приемника
и собственных часов приемника  относительно показаний часов системы
относительно показаний часов системы  :
:
 ;
; 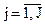 . (3.2.6)
. (3.2.6)
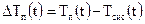 , (3.2.7)
, (3.2.7)
Используя (3.2.6), (3.2.7), показания часов j-го спутника  и показания собственных часов приемника
и показания собственных часов приемника  на любой момент физического времени t могут быть следующим образом выражены через смещения
на любой момент физического времени t могут быть следующим образом выражены через смещения  ,
,  :
:
 ;
;  . (3.2.8)
. (3.2.8)
 , (3.2.9)
, (3.2.9)
Подставляя (3.2.8), (3.2.9) в (3.2.5), получаем следующее выражение для псевдозадержки, измеренной (оцененной) в момент  (см. также учебное пособие [2]):
(см. также учебное пособие [2]):

 (3.2.10)
(3.2.10)
где
 (3.2.11)
(3.2.11)
– приращение показаний часов системы на интервале времени  , длительность которого равна задержке
, длительность которого равна задержке  распространения сигнала от точки, занимаемой j-м спутником в момент предшествия
распространения сигнала от точки, занимаемой j-м спутником в момент предшествия  , до точки, занимаемой приемником в момент измерения
, до точки, занимаемой приемником в момент измерения  .
.
На рис. 3.2.2 показано изменение псевдозадержек как функций физического времени t для двух спутников с номерами j и k. Для построения графиков, показанных на этом рисунке, использовано выражение (3.2.10).

Рис. 3.2.2 Изменение псевдозадержек как функций физического времени t

Оценка псевдодальности  по j-му спутнику определяется как произведение оценки псевдозадержки
по j-му спутнику определяется как произведение оценки псевдозадержки  (3.2.10) на скорость света с:
(3.2.10) на скорость света с:
 ,
,  . (3.2.12)
. (3.2.12)
где  дальность между точками, которые занимал j-й спутник в момент предшествия
дальность между точками, которые занимал j-й спутник в момент предшествия  и приемник в момент измерения
и приемник в момент измерения  .
.
Выражая дальность  в (3.2.12) через координаты
в (3.2.12) через координаты  ,
,  ,
,  точки, которую приемник занимал в момент измерения
точки, которую приемник занимал в момент измерения  , и координатами
, и координатами 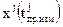 ,
, 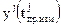 ,
, 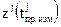 точки, которую занимал j-й спутник в момент предшествия
точки, которую занимал j-й спутник в момент предшествия  , получаем искомую функциональную связь (см. также учебное пособие [2])
, получаем искомую функциональную связь (см. также учебное пособие [2])
 (3.2.13)
(3.2.13)
Решение задачи 3.3
Особенность определения координат объекта радиотехническими средствами заключается в том, что при этом эти координаты непосредственно не измеряются. Непосредственно измеряются параметры радиосигналов, используемых для того или иного вида измерений. Измеренные параметры радиосигналов являются функциями координат объекта. Так, например, измерение задержки сигнала зависит от дальности до объекта, которая является функцией его координат. Определение же координат осуществляется путем вторичной обработки измерений, в основе которой лежит использование функциональных связей оцениваемых координат с измеренными значениями параметров радиосигнала.
Обозначим символом z измеряемый параметр радиосигнала, а символом x вектор оцениваемых величин, от которых зависит этот параметр. Под оцениваемыми величинами понимаются координаты объекта. В реальной практике могут существовать измерения z, которые зависят не только от координат, но и от дополнительных величин. Например, измерение псевдодальности зависит не только от координат навигационного приемника, но и от выраженного в метрах смещения 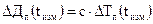 показаний часов приемника относительно показаний часов системы (см. формулу (3.2.13) в задаче 3.2). В процессе вторичной обработки таких измерений приходится оценивать не только координаты, но и все те дополнительные величины, от которых зависит измеряемый параметр z. Поэтому далее в число компонент вектора оцениваемых величин x будем включать не только координаты навигационного приемника, но и смещение
показаний часов приемника относительно показаний часов системы (см. формулу (3.2.13) в задаче 3.2). В процессе вторичной обработки таких измерений приходится оценивать не только координаты, но и все те дополнительные величины, от которых зависит измеряемый параметр z. Поэтому далее в число компонент вектора оцениваемых величин x будем включать не только координаты навигационного приемника, но и смещение  показаний его часов относительно показаний часов системы.
показаний его часов относительно показаний часов системы.
Введем в рассмотрение функцию
 (3.3.1)
(3.3.1)
связи измеряемого параметра z с вектором оцениваемых величин x. Если в (3.3.1) зафиксировать значение измеряемого параметра z и допустить произвольную вариацию компонент вектора x, то тогда (3.3.1) может рассматриваться как уравнение поверхности в пространстве компонент вектора x. В радиолокации эту поверхность принято называть поверхностью положения. При произвольном перемещении точки, координаты которой задаются компонентами вектора x, по поверхности положения значение измеряемого параметра z остается неизменным.
Поверхности положения играют важную роль в определении точности оценивания компонент вектора x. Такое оценивание в случае обработки не избыточных измерений геометрически интерпретируется как нахождение координат точки пересечения всех поверхностей положения. При избыточном числе измерений в общем случае поверхности положения не пересекаются в единственной точке. В этом случае в качестве оценки  вектора x принимаются координаты точки, наименьшим образом отклоняющейся от всех имеющихся поверхностей положения. Таким образом, видим, что точность оценивания компонент вектора x зависит не только от точности измерений параметра z, но и от свойств поверхностей положения в окрестности оценки
вектора x принимаются координаты точки, наименьшим образом отклоняющейся от всех имеющихся поверхностей положения. Таким образом, видим, что точность оценивания компонент вектора x зависит не только от точности измерений параметра z, но и от свойств поверхностей положения в окрестности оценки  . Указанные свойства определяют понятие геометрического фактора навигационной системы.
. Указанные свойства определяют понятие геометрического фактора навигационной системы.
Рассмотрим поверхности положения для измерений псевдодальностей. Из формулы (3.2.13), выведенной в решении задачи 3.2., получаем следующее выражение:
 , (3.3.2)
, (3.3.2)
где  ‑ выраженное в метрах смещение показаний часов приемника относительно показаний часов системы. Величина
‑ выраженное в метрах смещение показаний часов приемника относительно показаний часов системы. Величина  вычисляется в приемнике на основе данных, извлекаемых из навигационного сообщения j-го спутника.
вычисляется в приемнике на основе данных, извлекаемых из навигационного сообщения j-го спутника.
Формула (3.3.2) устанавливает связь поправленного измерения псевдодальности  с координатами приемника
с координатами приемника 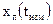 ,
,  ,
,  и смещением
и смещением  показаний его часов. Введенный ранее в рассмотрение вектор оцениваемых параметров x в данном случае будет состоять из 4-х компонент
показаний его часов. Введенный ранее в рассмотрение вектор оцениваемых параметров x в данном случае будет состоять из 4-х компонент
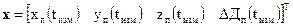 . (3.3.3)
. (3.3.3)
Таким образом, поверхность положения для измерений псевдодальностей должна изображаться в четырехмерном пространстве. Представить такую поверхность в наглядном виде невозможно. Поэтому мы рассмотрим упрощенный случай «плоской радионавигации», в котором оцениванию будет подвергаться трехкомпонентный вектор x вида (см. также учебное пособие [2])
 . (3.3.4)
. (3.3.4)
Для трехкомпонентного вектора x уравнение связи (3.3.2) преобразуется к виду
 .
.  (3.3.5)
(3.3.5)
Для изображения поверхности положения, соответствующей уравнению (3.3.5), представим его в более удобной форме:

 (3.3.6)
(3.3.6)
Положив в (3.3.6)  , получаем уравнение сечения поверхности положения плоскостью
, получаем уравнение сечения поверхности положения плоскостью  ,
,  системы координат, показанной на рис. 3.3.1:
системы координат, показанной на рис. 3.3.1:
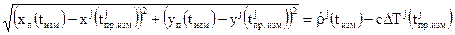 ,
,  . (3.3.7)
. (3.3.7)
Очевидно, что (3.3.7) является уравнением окружности с радиусом, равным  , и центром, расположенным в точке с координатами
, и центром, расположенным в точке с координатами  ,
,  , которая лежит в плоскости
, которая лежит в плоскости  ,
,  системы координат. Если теперь в уравнении (3.3.6) положить
системы координат. Если теперь в уравнении (3.3.6) положить  , то получаем уравнение
, то получаем уравнение

 , (3.3.8)
, (3.3.8)
сечения поверхности положения плоскостью, параллельной плоскости  ,
,  системы координат, поднятой над нею на высоту
системы координат, поднятой над нею на высоту  . Уравнению (3.3.8) удовлетворяет единственная точка с координатами
. Уравнению (3.3.8) удовлетворяет единственная точка с координатами  ,
,  , т. е сечением поверхности положения плоскостью, задаваемой уравнением
, т. е сечением поверхности положения плоскостью, задаваемой уравнением  , является точка с координатами
, является точка с координатами  ,
,  ,
,  .
.

Рис. 3.3.1 Поверхность положения измерений псевдодальностей для «навигации в плоскости»
Из приведенного рассмотрения следует, что уравнения (3.3.5), (3.3.6) являются уравнением конуса, показанного на рис. 3.3.1. Координаты точки пересечения трех таких конусов, показанной на рис. 3.3.2, определяет координаты  ,
,  местоположения приемника на плоскости и смещение
местоположения приемника на плоскости и смещение  показаний его часов относительно показаний часов системы.
показаний его часов относительно показаний часов системы.

Рис. 3.3.2 Пересечение поверхностей положения измерений псевдодальностей при радионавигации в плоскости
По аналогии с плоской радионавигацией заключаем, что исходное уравнение (3.3.2) задает в четырехмерном пространстве переменных  ,
,  ,
,  ,
,  поверхность положения в виде четырехмерного конуса. В сечении этого конуса трехмерной плоскостью
поверхность положения в виде четырехмерного конуса. В сечении этого конуса трехмерной плоскостью  ,
,  ,
,  системы координат лежит трехмерная сфера с радиусом
системы координат лежит трехмерная сфера с радиусом 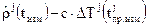 и центром, расположенным в точке с координатами
и центром, расположенным в точке с координатами  ,
,  ,
,  . Вершина конуса располагается в точке с координатами
. Вершина конуса располагается в точке с координатами  ,
,  ,
,  ,
, 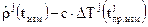 .
.
Решение задачи 3.4
Когда речь идет о количественном значении времени, в радионавигационных системах вообще и в спутниковой радионавигации в частности, используется не само время, а так называемое время по шкале системы, под которым понимается показания часов системы  на каждый момент физического времени t. Таким образом, для вычисления координат спутников на момент предшествия
на каждый момент физического времени t. Таким образом, для вычисления координат спутников на момент предшествия  в приемнике необходимо определить показания часов системы
в приемнике необходимо определить показания часов системы  на этот момент.
на этот момент.
В момент измерения  в приемнике осуществляется формирование оценок
в приемнике осуществляется формирование оценок 
 показаний часов всех отслеживаемого им спутников на соответствующие этим спутникам моменты предшествия
показаний часов всех отслеживаемого им спутников на соответствующие этим спутникам моменты предшествия  (см. решение задачи 3.1). По этим оценкам приемник вычисляет оценки псевдозадержек
(см. решение задачи 3.1). По этим оценкам приемник вычисляет оценки псевдозадержек  , относящиеся к моменту измерения
, относящиеся к моменту измерения 
 ,
,  (3.4.1)
(3.4.1)
где  ‑ показания собственных часов приемника в момент измерения
‑ показания собственных часов приемника в момент измерения  . Для дальнейшей обработки приемник сообщает измеренное значение псевдозадержки
. Для дальнейшей обработки приемник сообщает измеренное значение псевдозадержки  и значение
и значение  , которое трактуется как количественное значение времени на момент измерения
, которое трактуется как количественное значение времени на момент измерения  . Оценка
. Оценка  при этом не сообщается. Таким образом, на каждый момент измерения
при этом не сообщается. Таким образом, на каждый момент измерения  имеются два числа – показания
имеются два числа – показания  собственных часов приемника и измеренное значение псевдозадержки
собственных часов приемника и измеренное значение псевдозадержки  , вычисленное по формуле (3.4.1).
, вычисленное по формуле (3.4.1).
Для вычисления координат спутников на моменты предшествия  в дальнейшей обработке осуществляется восстановление значени1
в дальнейшей обработке осуществляется восстановление значени1 
 по формуле, вытекающей из (3.4.1)
по формуле, вытекающей из (3.4.1)
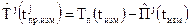 ,
,  (3.4.2)
(3.4.2)
и вычисление оценок 
 показаний часов системы на моменты предшествия
показаний часов системы на моменты предшествия 
 ,
,  (3.4.3)
(3.4.3)
где знак + относится к системе ГЛОНАСС, а – к GPS,  ‑ поправка для перехода со шкалы времени j-го спутника на шкалу системы, вычисляемая в приемнике путем использования полиномиальной модели, параметры которой передаются в навигационном сообщении каждого спутника. Значение оценки
‑ поправка для перехода со шкалы времени j-го спутника на шкалу системы, вычисляемая в приемнике путем использования полиномиальной модели, параметры которой передаются в навигационном сообщении каждого спутника. Значение оценки  (3.4.3) используется для вычисления координат j-го спутника на момент предшествия
(3.4.3) используется для вычисления координат j-го спутника на момент предшествия  .
.
Параметры математической модели, описывающей движение спутников системы ГЛОНАСС, привязаны не к шкале времени системы, а к шкале московского декретного времени (МДВ). Поэтому для вычисления координат спутников системы ГЛОНАСС на моменты предшествия  необходимо использовать не показания часов системы
необходимо использовать не показания часов системы  , а показания часов МДВ
, а показания часов МДВ  на те же моменты. Эти показания вычисляются по формуле
на те же моменты. Эти показания вычисляются по формуле
 ,
,  (3.4.4)
(3.4.4)
где τс – поправка для перехода со шкалы времени системы ГЛОНАСС на шкалу МДВ, передаваемая в составе навигационного сообщения спутников системы ГЛОНАСС.
Решение задачи 3.5
Координаты приемника  ,
,  ,
,  и координаты спутника
и координаты спутника  ,
, 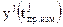 ,
,  в формуле (3.5.2) из условия задачи, задаются в разных системах координат, определяемых на рис. 3.5.1 осями
в формуле (3.5.2) из условия задачи, задаются в разных системах координат, определяемых на рис. 3.5.1 осями  ,
,  и
и  ,
,  соответственно.
соответственно.

Рис. 3.5.1. Положение гринвичской системы координат в моменты измерения и предшествия
По этой причине квадратный корень в формуле (3.5.2) из условия задачи 3.5, выражает не расстояние  между приемником и j-м спутником, а расстояние
между приемником и j-м спутником, а расстояние 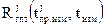 между приемником и гипотетической точкой (рис. 3.5.1), координаты которой в системе координат, задаваемой осями
между приемником и гипотетической точкой (рис. 3.5.1), координаты которой в системе координат, задаваемой осями  ,
,  , равны координатам
, равны координатам  ,
,  ,
,  j-го спутника, определяемым по эфемеридным данным на момент предшествия
j-го спутника, определяемым по эфемеридным данным на момент предшествия  .
.
Для нахождения правильного выражения для расстояния  , необходимо вычисленные по эфемеридным данным координаты спутников
, необходимо вычисленные по эфемеридным данным координаты спутников  ,
,  пересчитать в систему координат, задаваемую осями
пересчитать в систему координат, задаваемую осями  ,
,  . Этот пересчет никак не связан с движением спутников на интервале времени
. Этот пересчет никак не связан с движением спутников на интервале времени  , а связан только с поворотом гринвичской системы координат на этом интервале.
, а связан только с поворотом гринвичской системы координат на этом интервале.
Вычисление координат  ,
,  ,
,  спутника может быть осуществлено с помощью обычного перехода из одной системы координат в другую [4]:
спутника может быть осуществлено с помощью обычного перехода из одной системы координат в другую [4]:
 (3.5.4)
(3.5.4)
где  – угол поворота;
– угол поворота;  =7,292115·10-5 с-1 – угловая скорость вращения Земли;
=7,292115·10-5 с-1 – угловая скорость вращения Земли;  – время распространения сигнала от j-го спутника до приемника.
– время распространения сигнала от j-го спутника до приемника.
Оценим максимальные возможные отличия, между исходными  ,
,  и пересчитанными
и пересчитанными  ,
,  координатами спутников (координата z не рассматривается потому, что
координатами спутников (координата z не рассматривается потому, что  ). Максимальное время распространения сигналов спутников не превышает 90 мс. За это время угол поворота Земли
). Максимальное время распространения сигналов спутников не превышает 90 мс. За это время угол поворота Земли  достигнет значения не превышающего ~
достигнет значения не превышающего ~  рад. С учетом того что радиусы орбит спутников равны ~
рад. С учетом того что радиусы орбит спутников равны ~  м, отличие координат
м, отличие координат  ,
,  от
от  ,
,  у спутников, проходящих в момент
у спутников, проходящих в момент  плоскость экватора, может доходить до ~ 173 м. Для столь малого угла
плоскость экватора, может доходить до ~ 173 м. Для столь малого угла  и
и  . Поэтому, вместо (3.5.4) вполне можно использовать более простые выражения:
. Поэтому, вместо (3.5.4) вполне можно использовать более простые выражения:
 (3.5.5)
(3.5.5)
Как видно из (3.5.4, 3.5.5) для пересчета координат спутников необходимо знать время распространения сигнала  . Это время можно вычислить, если знать координаты приемника. Таким образом, для определения координат приемника надо знать время распространения сигнала
. Это время можно вычислить, если знать координаты приемника. Таким образом, для определения координат приемника надо знать время распространения сигнала 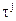 , а для вычисления времени
, а для вычисления времени  надо знать координаты приемника. То есть возникает замкнутый круг.
надо знать координаты приемника. То есть возникает замкнутый круг.
Можно предложить два способа для выхода из этого замкнутого круга (см. также учебное пособие [2]). Оба способа основаны на том, что процесс вычисления координат и смещения показаний часов приемника относительно часов системы по измерениям псевдозадержек является итерационным.
В первом способе вначале итерационный процесс, т. е. определение координат и смещения показаний часов приемника относительно часов системы, осуществляется без пересчета координат спутников. С учетом того что большинство спутников в моменты  ,
,  не находятся в плоскости экватора, после окончания итерационного процесса будут получены оценки
не находятся в плоскости экватора, после окончания итерационного процесса будут получены оценки  ,
,  ,
, 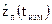 координат приемника с ошибками не превышающими ~100 м. Дальности до спутников, вычисленные по найденным таким образом оценкам, будут содержать ошибки, также не превышающие ~100 м. Следовательно, ошибки вычисления времен распространения сигналов
координат приемника с ошибками не превышающими ~100 м. Дальности до спутников, вычисленные по найденным таким образом оценкам, будут содержать ошибки, также не превышающие ~100 м. Следовательно, ошибки вычисления времен распространения сигналов  ,
, 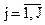 до спутников не будут превышать величины ~
до спутников не будут превышать величины ~  с. Это будет, в свою очередь, вносить ошибки в определение углов поворота
с. Это будет, в свою очередь, вносить ошибки в определение углов поворота 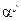 ~
~  рад. Столь малыми ошибками вычисления углов поворота
рад. Столь малыми ошибками вычисления углов поворота 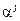 , можно пренебречь. Поэтому после окончания итерационного вычислительного процесса, в котором используются не пересчитанные координаты спутников, рассчитываются дальности до спутников, времена распространения сигналов
, можно пренебречь. Поэтому после окончания итерационного вычислительного процесса, в котором используются не пересчитанные координаты спутников, рассчитываются дальности до спутников, времена распространения сигналов  и углы поворота
и углы поворота  , где
, где  – угловая скорость вращения Земли. Далее осуществляется пересчет координат спутников по формулам (3.5.4) либо (3.5.5) и после этого делается одна дополнительная итерация, в которой используются уже пересчитанные координаты спутников.
– угловая скорость вращения Земли. Далее осуществляется пересчет координат спутников по формулам (3.5.4) либо (3.5.5) и после этого делается одна дополнительная итерация, в которой используются уже пересчитанные координаты спутников.
Во втором способе вращение Земли учитывается путем введения в измерения псевдодальностей поправок, рассчитываемых заново на каждой итерации. С целью получения формулы для вычисления этих поправок, введем в рассмотрение некоторую плавающую точку, координаты которой в повернутой системе координат  обозначим как
обозначим как  ,
,  ,
,  . Тогда расстояние между точкой с координатами
. Тогда расстояние между точкой с координатами 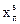 ,
,  ,
,  , которую последовательно занимает приемник на каждой s-й итерации в процессе поиска решения, и плавающей точкой может быть выражено с помощью следующей функции переменных
, которую последовательно занимает приемник на каждой s-й итерации в процессе поиска решения, и плавающей точкой может быть выражено с помощью следующей функции переменных  ,
,  ,
, 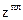 :
:
 . (3.5.6)
. (3.5.6)
Разложим функцию  в ряд Тейлора в гипотетической точке, т. е. точке с координатами
в ряд Тейлора в гипотетической точке, т. е. точке с координатами  ,
,  ,
,  , где учтем члены в степени не выше первой:
, где учтем члены в степени не выше первой:
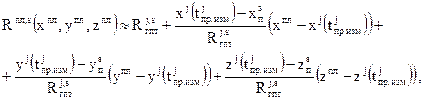 (3.5.7)
(3.5.7)
где  – расстояние между точкой, занимаемой приемником на s-й итерации, и гипотетической точкой.
– расстояние между точкой, занимаемой приемником на s-й итерации, и гипотетической точкой.
Совместим теперь плавающую точку с точкой, занимаемой на рис. 3.5.1 j-м спутником, и вычислим расстояние 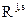 между точкой, занимаемой приемником на s-й итерации, и j-м спутником с помощью линеаризованного выражения 7). С этой целью подставим в (3.5.7) вместо координат
между точкой, занимаемой приемником на s-й итерации, и j-м спутником с помощью линеаризованного выражения 7). С этой целью подставим в (3.5.7) вместо координат  ,
, 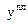 ,
, 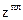 плавающей точки координаты j-го спутника, определяемые выражениями (3.5.5):
плавающей точки координаты j-го спутника, определяемые выражениями (3.5.5):
 ,
,  . (3.5.8)
. (3.5.8)
С учетом того что 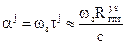 , выражение (3.5.8) преобразуется к виду
, выражение (3.5.8) преобразуется к виду
 .
. 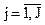 (3.5.9)
(3.5.9)
Из (3.5.9) нетрудно видеть, что дальность до гипотетической точки 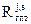 на s-й итерации может быть следующим образом выражена через дальность
на s-й итерации может быть следующим образом выражена через дальность  до истинного положения j-го спутника в повернутой системе координат
до истинного положения j-го спутника в повернутой системе координат  :
:
 ,
,  , (3.5.10)
, (3.5.10)
где поправка  вычисляется по формуле
вычисляется по формуле
 ,
,  . (3.5.11)
. (3.5.11)
Добавление на каждой s-й итерации поправки  (3.5.11) к измерениям псевдодальностей эквивалентно переносу истинного положения каждого j-го спутника в соответствующую ему гипотетическую точку. Но координаты гипотетических точек в повернутой системе равны координатам соответствующих им спутников в исходных системах. Поэтому учет поправок
(3.5.11) к измерениям псевдодальностей эквивалентно переносу истинного положения каждого j-го спутника в соответствующую ему гипотетическую точку. Но координаты гипотетических точек в повернутой системе равны координатам соответствующих им спутников в исходных системах. Поэтому учет поправок  (3.5.11) в измерениях псевдодальностей позволяет использовать в итерационном процессе исходные координаты спутников.
(3.5.11) в измерениях псевдодальностей позволяет использовать в итерационном процессе исходные координаты спутников.
Решение задачи 3.6
Для обработки измерений псевдодоплеровских смещений частот несущих колебаний спутниковых сигналов с целью определения составляющих  ,
,  ,
,  вектора
вектора  скорости приемника, необходимо найти функциональную связь этих составляющих с результатами измерений псевдодоплеровских смещений. Как известно из курса радиолокации, доплеровское смещение
скорости приемника, необходимо найти функциональную связь этих составляющих с результатами измерений псевдодоплеровских смещений. Как известно из курса радиолокации, доплеровское смещение  , входящее в формулу (3.6.1) из условия задачи 3.6, следующим образом связано с радиальной скоростью
, входящее в формулу (3.6.1) из условия задачи 3.6, следующим образом связано с радиальной скоростью  движения приемника относительно j-го спутника
движения приемника относительно j-го спутника

 (3.6.2)
(3.6.2)
где  ‑ длина волны несущего колебания, излучаемого j-м спутником. Подставляя (3.6.2) в (3.6.1), получаем следующее выражение для псевдодоплеровского смещения
‑ длина волны несущего колебания, излучаемого j-м спутником. Подставляя (3.6.2) в (3.6.1), получаем следующее выражение для псевдодоплеровского смещения
 ,
,  (3.6.3)
(3.6.3)
Для того чтобы по измерениям (оценкам) 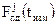
 можно было бы определять составляющие вектора скорости приемника в момент времени
можно было бы определять составляющие вектора скорости приемника в момент времени  , необходимо значение радиальной скорости
, необходимо значение радиальной скорости  выразить как функцию координат
выразить как функцию координат  ,
,  ,
,  и составляющих вектора скорости
и составляющих вектора скорости  ,
,  ,
,  приемника на момент времени
приемника на момент времени  , а также как функцию координат
, а также как функцию координат  ,
,  ,
,  и составляющих вектора скорости j-го КА
и составляющих вектора скорости j-го КА  ,
,  ,
, 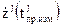 на момент времени
на момент времени  (см. также учебное пособие [2]).
(см. также учебное пособие [2]).
На рис. 3.6.1 точками показано расположение приемника и j-го КА в моменты времени измерения  и предшествия моменту измерения
и предшествия моменту измерения  соответственно. Символами
соответственно. Символами  и
и  обозначены вектора скорости приемника
обозначены вектора скорости приемника  и j-го КА
и j-го КА  в моменты
в моменты  и
и  соответственно. В связи с малостью различия составляющих скоростей спутника и приемника в абсолютной инерциальной и вращающейся гринвичской системах координат, рис. 3.6.1, который строго говоря, должен рассматриваться в абсолютной инерциальной системе, будет рассматриваться нами во вращающейся гринвичской системе координат.
соответственно. В связи с малостью различия составляющих скоростей спутника и приемника в абсолютной инерциальной и вращающейся гринвичской системах координат, рис. 3.6.1, который строго говоря, должен рассматриваться в абсолютной инерциальной системе, будет рассматриваться нами во вращающейся гринвичской системе координат.
Разность  обозначает вектор скорости движения приемника относительно j-го КА.
обозначает вектор скорости движения приемника относительно j-го КА.

 (3.6.4)
(3.6.4)

Рис. 3.6.1 Движение приемника относительно j-го спутника
Радиальная скорость  движения приемника относительно j-го КА является проекцией разности
движения приемника относительно j-го КА является проекцией разности  на прямую, соединяющую точки расположения приемника и j-го КА. Количественно эту проекцию можно рассматривать как скалярное произведение разности векторов
на прямую, соединяющую точки расположения приемника и j-го КА. Количественно эту проекцию можно рассматривать как скалярное произведение разности векторов  на единичный вектор h, ориентированный из точки расположения приемника на j-й КА. Как известно, скалярное произведение двух векторов можно представить в виде суммы проекций этих векторов на одинаковые оси системы координат. Это позволяет записать для радиальной скорости
на единичный вектор h, ориентированный из точки расположения приемника на j-й КА. Как известно, скалярное произведение двух векторов можно представить в виде суммы проекций этих векторов на одинаковые оси системы координат. Это позволяет записать для радиальной скорости  следующее выражение
следующее выражение
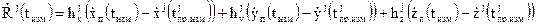
 (3.6.5)
(3.6.5)
где  ,
,  ,
,  – направляющие косинусы единичного вектора
– направляющие косинусы единичного вектора  , ориентированного из точки расположения приемника в точку расположения j-го КА:
, ориентированного из точки расположения приемника в точку расположения j-го КА:

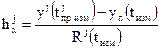
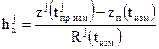
 (3.6.6)
(3.6.6)
 – расстояние между приемником и j-м КА. Нетрудно убедиться, что
– расстояние между приемником и j-м КА. Нетрудно убедиться, что  . Это означает, что вектор
. Это означает, что вектор  , компоненты которого вычисляются по формулам (3.6.6), является единичным.
, компоненты которого вычисляются по формулам (3.6.6), является единичным.
Подставляя (3.6.5) в (3.6.3), получаем следующую линейную связь псевдодоплеровского смещения  частоты несущего колебания j-го КА с составляющими вектора скорости приемника
частоты несущего колебания j-го КА с составляющими вектора скорости приемника  ,
,  ,
,  и смещением
и смещением  частоты его задающего генератора
частоты его задающего генератора

 (3.6.7)
(3.6.7)
Вследствие того, что связь (3.6.7) псевдодоплеровского смещения  частоты несущего колебания j-го КА с составляющими вектора скорости приемника
частоты несущего колебания j-го КА с составляющими вектора скорости приемника  ,
,  ,
,  и смещением
и смещением  частоты его задающего генератора является линейной, поверхности положений измерений псевдодоплеровских смещений частот несущих колебаний сигналов КА являются трехмерными плоскостями в четырехмерном пространстве.
частоты его задающего генератора является линейной, поверхности положений измерений псевдодоплеровских смещений частот несущих колебаний сигналов КА являются трехмерными плоскостями в четырехмерном пространстве.
Из (3.6.7) получаем следующую, в общем случае избыточную систему из J (J – общее количество КА, одновременно отслеживаемых приемником) линейных уравнений относительно переменных  ,
,  ,
,  ,
,  :
:
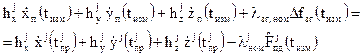
 , (3.6.8)
, (3.6.8)
где  – номинальная длина волны сигнала задающего генератора приемника,
– номинальная длина волны сигнала задающего генератора приемника,  ‑ измеренное (т. е. содержащее погрешности измерений) значение псевдодоплеровского смещения по j-му КА.
‑ измеренное (т. е. содержащее погрешности измерений) значение псевдодоплеровского смещения по j-му КА.
Поскольку система (3.6.8) является линейной, ее решение может быть записано в аналитической форме. Для этого введем в рассмотрение следующие векторно-матричные обозначения:
 ; (3.6.9)
; (3.6.9)
 ; (3.6.10)
; (3.6.10)
 , (3.6.11)
, (3.6.11)
где составляющие  ,
,  , вектора
, вектора  равны правым частям уравнений (3.6.8):
равны правым частям уравнений (3.6.8):

 . (3.6.12)
. (3.6.12)
Тогда система линейных уравнений (3.6.8) переписывается в следующем матричном виде
 . (3.6.13)
. (3.6.13)
При измерении псевдодоплеровских смещений относительно 4-х КА оценки  ,
,  ,
, 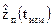 ,
,  компонент вектора
компонент вектора  (3.6.10) определяются как координаты точки пересечения 4-х поверхностей положения, каждая из которых является 3-х мерной плоскостью в четырехмерном пространстве. В этом случае решение системы (3.6.13) записывается в виде:
(3.6.10) определяются как координаты точки пересечения 4-х поверхностей положения, каждая из которых является 3-х мерной плоскостью в четырехмерном пространстве. В этом случае решение системы (3.6.13) записывается в виде:
 . (3.6.14)
. (3.6.14)
Однако на практике число КА, по которым ведутся измерения, обычно больше 4-х. В этом случае мы будем иметь более 4-х поверхностей положения, каждая из которых является 3‑х мерной плоскостью в четырехмерном пространстве. В общем случае все эти плоскости не будут пересекаться в единственной точке, т. е. возникает задача решения системы избыточных линейных уравнений. В этой ситуации используется решение наименьших квадратов, т. е. в качестве решения принимаются координаты точки, которая не лежит на поверхности ни одной из трехмерных плоскостей, но сумма квадратов уклонений этой точки от поверхностей всех этих плоскостей является минимальной. Такое решение находится с помощью метода псевдообратной матрицы:
 . (3.6.15)
. (3.6.15)
Измерения, полученные по разным КА, могут при обработке учитываться с разными весами. В этом случае решение системы (3.6.13) записывается в виде:
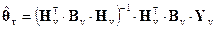 , (3.6.16)
, (3.6.16)
где  – весовая матрица, которая обычно вычисляется как матрица, обратная к ковариационной матрице
– весовая матрица, которая обычно вычисляется как матрица, обратная к ковариационной матрице  ошибок компонент вектора
ошибок компонент вектора  (3.6.11).
(3.6.11).
Элементами вектора  являются оценки
являются оценки  ,
,  ,
,  составляющих вектора скорости приемника и оценка
составляющих вектора скорости приемника и оценка  смещения частоты его задающего генератора. Относительная величина
смещения частоты его задающего генератора. Относительная величина  может рассматриваться как оценка скорости смещения показаний часов приемника относительно показаний часов системы (скорости смещения шкалы времени приемника относительно шкалы системы). Действительно, сигнал секундных меток шкалы времени приемника формируется путем деления частоты
может рассматриваться как оценка скорости смещения показаний часов приемника относительно показаний часов системы (скорости смещения шкалы времени приемника относительно шкалы системы). Действительно, сигнал секундных меток шкалы времени приемника формируется путем деления частоты  его задающего генератора на постоянный коэффициент
его задающего генератора на постоянный коэффициент  , численно равный номинальному значению
, численно равный номинальному значению  этой частоты. Отсюда оценку отклонения частоты сигнала секундных меток приемника от номинального значения в 1 Гц можно определить как
этой частоты. Отсюда оценку отклонения частоты сигнала секундных меток приемника от номинального значения в 1 Гц можно определить как  , а оценку самой частоты секундных меток приемника как
, а оценку самой частоты секундных меток приемника как  Гц. Эту частоту можно рассматривать как угловую скорость вращения секундной стрелки часов приемника в момент времени
Гц. Эту частоту можно рассматривать как угловую скорость вращения секундной стрелки часов приемника в момент времени  . Положим, для простоты, что эта угловая скорость остается постоянной. Тогда на интервале времени в 1 с секундная стрелка часов приемника повернется на угол равный
. Положим, для простоты, что эта угловая скорость остается постоянной. Тогда на интервале времени в 1 с секундная стрелка часов приемника повернется на угол равный  цикла (замена
цикла (замена  на
на  была проведена для того чтобы устранить несоответствие в размерностях), или, иными словами, показания часов приемника на интервале времени в 1 с прирастают на
была проведена для того чтобы устранить несоответствие в размерностях), или, иными словами, показания часов приемника на интервале времени в 1 с прирастают на  оборота. Отсюда видим, что на каждой секунде шкалы системы показания часов приемника будут отстраиваться на
оборота. Отсюда видим, что на каждой секунде шкалы системы показания часов приемника будут отстраиваться на  с и, следовательно, скорость расстройки оценивается как безразмерная величина
с и, следовательно, скорость расстройки оценивается как безразмерная величина  .
.
Наличие оценки  смещения частоты задающего генератора приемника позволяет строить аппаратуру ее компенсации. На этой основе могут быть разработаны генераторы с очень высокой долговременной стабильностью частоты.
смещения частоты задающего генератора приемника позволяет строить аппаратуру ее компенсации. На этой основе могут быть разработаны генераторы с очень высокой долговременной стабильностью частоты.
Оценка  скорости смещения показаний часов приемника относительно показаний часов системы используется в приемнике для формирования измерений привязанных к моментам времени, задаваемым показаниями определенных внешних часов. Это достигается путем такой модификации собственных часов приемника на основе использования оценки
скорости смещения показаний часов приемника относительно показаний часов системы используется в приемнике для формирования измерений привязанных к моментам времени, задаваемым показаниями определенных внешних часов. Это достигается путем такой модификации собственных часов приемника на основе использования оценки  , что их показания в каждый момент физического времени с ошибками в доли микросекунды совпадают с показаниями внешних часов (обычно это часы системы). В результате появляется возможность синхронизации с ошибками в доли микросекунды моментов формирования измерений в нескольких разнесенных на большие расстояния и электрически не связанных между собою приемниках.
, что их показания в каждый момент физического времени с ошибками в доли микросекунды совпадают с показаниями внешних часов (обычно это часы системы). В результате появляется возможность синхронизации с ошибками в доли микросекунды моментов формирования измерений в нескольких разнесенных на большие расстояния и электрически не связанных между собою приемниках.
Приложение C
Определение точности оценок, получаемых методом наименьших квадратов
На практике часто возникает задача оценки точности параметров, получаемых в результате обработки измерений методом наименьших квадратов. Наиболее распространенная оценка точности скалярного параметра сводится к определению его дисперсии. В случае оценки векторного параметра  необходимо определить точность оценивания m его компонент. Для этого необходимо вычислить ковариационную матрицу этих компонент. Необходимость вычисления ковариационной матрицы объясняется тем, что ошибки определения компонент оцениваемого вектора взаимосвязаны и зависят как от точности всех измерений, так и от геометрических свойств (геометрического фактора) функций
необходимо определить точность оценивания m его компонент. Для этого необходимо вычислить ковариационную матрицу этих компонент. Необходимость вычисления ковариационной матрицы объясняется тем, что ошибки определения компонент оцениваемого вектора взаимосвязаны и зависят как от точности всех измерений, так и от геометрических свойств (геометрического фактора) функций  связи измерений
связи измерений  с оцениваемым вектором
с оцениваемым вектором  в окрестности значений оцениваемого вектора (см. приложение A).
в окрестности значений оцениваемого вектора (см. приложение A).
Наиболее просто искомая ковариационная матрица компонент векторного параметра вычисляется в случае линейности функций  связи измерений
связи измерений  с оцениваемым вектором
с оцениваемым вектором  (линейности вектор-функции-столбца
(линейности вектор-функции-столбца  (A.7) в приложении A). Рассмотрим случай линейного оценивания по наиболее общей формуле (A.30) из приложения A. Для этого введем в рассмотрение вектор
(A.7) в приложении A). Рассмотрим случай линейного оценивания по наиболее общей формуле (A.30) из приложения A. Для этого введем в рассмотрение вектор  ошибок компонент вектора измерений
ошибок компонент вектора измерений  . В соответствии с общей формулой (A.30) вектор
. В соответствии с общей формулой (A.30) вектор  ошибок компонент линейной векторной оценки
ошибок компонент линейной векторной оценки  может быть вычислен так
может быть вычислен так
 , (C.1)
, (C.1)
где
 (C.2)
(C.2)
(N×m)-матрица, независимая от оцениваемого вектора  вследствие линейности вектор-функции-столбца
вследствие линейности вектор-функции-столбца  .
.
 ‑ N-вектор ошибок измерений, ковариационная матрица
‑ N-вектор ошибок измерений, ковариационная матрица  которого предполагается заданной.
которого предполагается заданной.
По определению, искомая ковариационная матрица  вектора ошибок
вектора ошибок  может быть вычислена так
может быть вычислена так
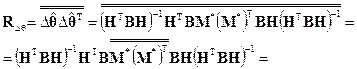 (C.3)
(C.3)
где двойная черта сверху означает операцию вычисления математического ожидания от всех элементов матрицы, стоящей под этой двойной чертой. Нетрудно видеть, что  . Подставляя в (C.3)
. Подставляя в (C.3)  вместо
вместо  и учитывая, что
и учитывая, что  , имеем
, имеем
 (C.4)
(C.4)
Таким образом, ковариационная матрица  ошибок линейной векторной оценки
ошибок линейной векторной оценки  (A.30) может быть вычислена с помощью очень простой формулы (C.4).
(A.30) может быть вычислена с помощью очень простой формулы (C.4).
Несколько более сложно вычисляются ковариационная матрица ошибок оценки  в случае нелинейности функций
в случае нелинейности функций  связи измерений
связи измерений  с оцениваемым вектором
с оцениваемым вектором  (нелинейности вектор-функции-столбца
(нелинейности вектор-функции-столбца  (A.7) в приложении A). Оценка
(A.7) в приложении A). Оценка  в этом случае вычисляется итерационным методом. На каждой s-й итерации по формуле (A.27) вычисляется вектор поправок
в этом случае вычисляется итерационным методом. На каждой s-й итерации по формуле (A.27) вычисляется вектор поправок
 (C.5)
(C.5)
 к оценке
к оценке  , найденной на предыдущей (s-1)-й итерации и далее оценка
, найденной на предыдущей (s-1)-й итерации и далее оценка  поправляется в соответствии с выражением
поправляется в соответствии с выражением  (A.21). Итерационный процесс продолжается до тех пор, пока модуль очередного вектора поправок к предыдущей оценке не станет достаточно малой величиной. В результате находится решение
(A.21). Итерационный процесс продолжается до тех пор, пока модуль очередного вектора поправок к предыдущей оценке не станет достаточно малой величиной. В результате находится решение  наименьших квадратов, минимизирующее сумму квадратов компонент вектора невязок.
наименьших квадратов, минимизирующее сумму квадратов компонент вектора невязок.
Описанный выше итерационный процесс будет сходиться к значению  независимо от приближения
независимо от приближения  , выбранного в качестве начального. Соответствующие процессы сходимости от разных начальных приближений
, выбранного в качестве начального. Соответствующие процессы сходимости от разных начальных приближений  и
и  для упрощенного двумерного случая иллюстрируются на рис. С.1
для упрощенного двумерного случая иллюстрируются на рис. С.1

Рисунок C.1 Сходимость из точки начального приближения в точку наименьших квадратов
Если процесс сходимости начать с истинного значения  , то он так же сойдется в точку
, то он так же сойдется в точку  . Поскольку оценка наименьших квадратов
. Поскольку оценка наименьших квадратов  близка к истинному значению, то допустимо полагать, что такая сходимость будет достигнута за одну итерацию. Но разность
близка к истинному значению, то допустимо полагать, что такая сходимость будет достигнута за одну итерацию. Но разность 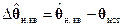 по определению является ошибкой вычисления оценки наименьших квадратов
по определению является ошибкой вычисления оценки наименьших квадратов 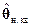 . Следовательно, если в формуле (C.5) матрицу
. Следовательно, если в формуле (C.5) матрицу  заменить на матрицу
заменить на матрицу  (т. е. заменить на матрицу
(т. е. заменить на матрицу  (A.23), вычисленную в точке
(A.23), вычисленную в точке  ), то формула (C.5) позволяет вычислять ошибку оценки наименьших квадратов
), то формула (C.5) позволяет вычислять ошибку оценки наименьших квадратов 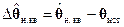 .
.
 (C.6)
(C.6)
Используя выражение (C.6) вычислим ковариационную матрицу  ошибок оценки
ошибок оценки  в случае нелинейности функций
в случае нелинейности функций  связи измерений
связи измерений  с оцениваемым вектором
с оцениваемым вектором  (нелинейности вектор-функции-столбца
(нелинейности вектор-функции-столбца  (A.7) в приложении A):
(A.7) в приложении A):
 , (C.7)
, (C.7)
где нижний индекс “ист” обозначает то, что соответствующие элементы вычислены в истинной точке  (т. е.
(т. е.  ,
,  ). С учетом того, что операция вычисления математического ожидания
). С учетом того, что операция вычисления математического ожидания 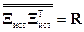 дает ковариационную матрицу
дает ковариационную матрицу  ошибок вектора невязок
ошибок вектора невязок  , из (C.7) получаем выражение
, из (C.7) получаем выражение
 (C.8)
(C.8)
для вычисления ковариационной матрицы  оценки наименьших квадратов в случае нелинейности функций
оценки наименьших квадратов в случае нелинейности функций  связи измерений
связи измерений  с оцениваемым вектором
с оцениваемым вектором  (нелинейности вектор-функции-столбца
(нелинейности вектор-функции-столбца  (A.7) в приложении A).
(A.7) в приложении A).
В реальной практике истинная оценка  конечно неизвестна. Поэтому вычисление матрицы
конечно неизвестна. Поэтому вычисление матрицы  (A.23) в истинной точке
(A.23) в истинной точке  заменяют ее вычислением в точке наименьших квадратов
заменяют ее вычислением в точке наименьших квадратов 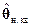 . В результате формула (C.8) преобразуется к виду
. В результате формула (C.8) преобразуется к виду
 (C.9)
(C.9)
где 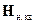 ‑ матрица
‑ матрица  (A.23), вычисленная в точке
(A.23), вычисленная в точке 
Поскольку оценка наименьших квадратов 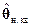 близка к истинной оценке
близка к истинной оценке  , такая подмена не вносит существенных искажений в вычисление характеристик ошибки
, такая подмена не вносит существенных искажений в вычисление характеристик ошибки  .
.
Дата добавления: 2018-11-24; просмотров: 255; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
