Эквивалентные бесконечно малые.
Сформулировать основные виды неопределенностей и способы их раскрытия
| Вид неопределенности | Правило раскрытия | ||
| 1. | 1.1. Чтобы раскрыть неопределенность вида  ,
заданную отношением двух многочленов, надо и числитель и знаменатель почленно разделить на переменную величину в наибольшей степени.
| ||
| 1.2. Для раскрытия неопределенности вида ,
заданную отношением иррациональных функций, надо и числитель и знаменатель почленно разделить на переменную величину в наибольшей степени с учетом степеней корней.
| |||
| 2. | 2.1. Для того, чтобы определить предел дробно-рациональной функции в случае, когда при x → a числитель и знаменатель дроби имеют пределы, равные нулю, надо числитель и знаменатель дроби разделить на x - a и перейти к пределу. Если и после этого числитель и знаменатель новой дроби имеют пределы, равные нулю при x → a, то надо произвести повторное деление на x - a. | ||
2.2. Чтобы раскрыть неопределенность вида  ,
в которой числитель или знаменатель иррациональны, следует надлежащим образом избавиться от иррациональности, умножив и числитель и знаменатель дроби на одно и то же выражение, приводящее к формулам сокращенного умножения. Неопределенность устраняется после сокращения дроби.
В случае квадратных корней и числитель и знаменатель дроби умножаются на сопряженное выражение тому, которое содержит иррациональность и применяется формула
a 2 – b 2 = ( a – b )( a + b ) .
В случае кубических корней и числитель и знаменатель дроби умножаются на неполный квадрат суммы или разности и применяется формула
a3 ± b3 = (a ± b)(a2 ± ab + b2).
| |||
| 3.
| 3.1. Неопределенность вида  ,
получающаяся в результате алгебраической суммы иррациональных выражений, устраняется или приводится к типу 1 путем домножения и деления на одно и то же выражение, приводящее к формулам сокращенного умножения.
В случае квадратных корней разность домножается на сопряженное выражение и применяется формула a 2 – b 2 = ( a – b )( a + b ) .
В случае кубических корней функция домножается на неполный квадрат суммы или разности и применяется формула a 3 ± b 3 = ( a ± b )( a 2 ± ab + b 2 ).
| ||
3.2. Неопределенность вида ,
получающаяся в результате алгебраической суммы двух дробей, устраняется или сводится к типу 2 путем приведения дробей к общему знаменателю.
Пусть:
 ,  .
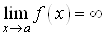Тогда:
 
| |||
| 4. Замечательные пределы |
4.1. Первый замечательный предел (неопределенность ).
В случае, когда под знаком предела стоят тригонометрические функции, дающие неопределенность , используется первый замечательный предел:
 .
Его различные формы:  ,  ,  ,
 ,  ,
 ,  .
| ||
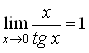4.2. Второй замечательный предел (неопределенность  ):
 .
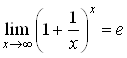Его различные формы:
 ,  ,  ,  , 
| |||
5. 
| 5.1. Неопределенность вида
сводится либо к неопределенности типа 1  , либо к неопределенности типа 2  путем перемещения в знаменатель одного из сомножителей.
Пусть
 ,  .
Тогда:
| ||
6.  , 
| 6.1. Неопределенности вида ,
сводятся к неопределенности типа 5 путем логарифмирования.
|
|
|
|
Эквивалентные бесконечно малые.
Эквивалентные - значит, равносильные. Во многих задачах на вычисление пределов можно заменить некоторую бесконечно малую эквивалентной бесконечно малой. Это здорово помогает упростить решение задачи и сократить время решения.
Доказана эквивалентность следующих важнейших бесконечно малых:
1) 
2) 
3) 
4) 
5) 
6) 
( 
)
7) 
8) 
( )
9) 
Пример. Привести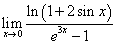 
к первому замечательному пределу путём использования эквивалентных бесконечно малых.
Решение. Применяя эквивалентные бесконечно малые и , получаем:
Таблица основных производных. Производная сложной функции
Производные основных элементарных функций.
1)С¢ = 0; 9) 
2)(xm)¢ = mxm-1; 10)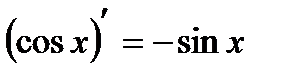 
3) 
11) 
|
|
|
4) 
12) 
5) 
13) 
6) 
14) 
7) 
15) 
8) 
16) 
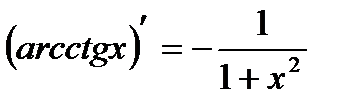
Производная сложной функции.
Теорема. Пусть y = f ( x ); u = g ( x ), причем область значений функции u входит в область определения функции f .
Тогда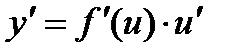 
Доказательство.
( с учетом того, что если Dx®0, то Du®0, т.к. u = g(x) – непрерывная функция)
Тогда 
Теорема доказана.
Таблица основных первообразных. Основные методы интегрирования.
| Интеграл | Значение | Интеграл | Значение | ||
| 1 | 
| -ln½cosx½+C | 9 | 
| ex + C |
| 2 | 
| ln½sinx½+ C | 10 | 
| sinx + C |
| 3 | 
| 
| 11 | 
| -cosx + C |
| 4 | 
| 
| 12 | 
| tgx + C |
| 5 | 
| 
| 13 | 
| -ctgx + C |
| 6 | 
| ln 
| 14 | 
| arcsin  + C
|
| 7 | 
| 
| 15 | 
| 
|
| 8 | 
| 
| 16 | 
| 
|
Методы интегрирования.
Рассмотрим три основных метода интегрирования.
|
|
|
Непосредственное интегрирование.
Метод непосредственного интегрирования основан на предположении о возможном значении первообразной функции с дальнейшей проверкой этого значения дифференцированием. Вообще, заметим, что дифференцирование является мощным инструментом проверки результатов интегрирования.
Рассмотрим применение этого метода на примере:
Требуется найти значение интеграла 
. На основе известной формулы дифференцирования 
можно сделать вывод, что искомый интеграл равен 
, где С – некоторое постоянное число. Однако, с другой стороны 
. Таким образом, окончательно можно сделать вывод:
Способ подстановки (замены переменных).
Теорема: Если требуется найти интеграл 
, но сложно отыскать первообразную, то с помощью замены x = j(t) и dx = j¢(t)dt получается:
Пример. Найти неопределенный интеграл 
.
Сделаем замену t = sinx, dt = cosxdt.
Интегрирование по частям.
Способ основан на известной формуле производной произведения:
(uv)¢ = u¢v + v¢u
где u и v – некоторые функции от х.
В дифференциальной форме: d(uv) = udv + vdu
Проинтегрировав, получаем: 
, а в соответствии с приведенными выше свойствами неопределенного интеграла:
или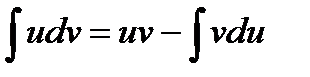 
;
Получили формулу интегрирования по частям, которая позволяет находить интегралы многих элементарных функций.
Пример. 
Как видно, последовательное применение формулы интегрирования по частям позволяет постепенно упростить функцию и привести интеграл к табличному.
Дата добавления: 2018-11-24; просмотров: 240; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!