Задачи повышенной трудности. Целочисленная арифметика.

Стр 1 из 18Следующая ⇒

Сборник задач по программированию

Линейные алгоритмы

Оператор присваивания и вывод данных

1. Присвоить переменной Х значение 20 и вывести

Х = ______ квадрат Х = ________

(вместо _____ надо вывести соответствующее значение)

2. Присвоить трем переменным целые нечетные числа, вычислить их сумму и вывести:

Вот некоторые нечетные числа:

_____ _______ ______

А вот их сумма: _________

3. Присвоить переменным А, В, С любые положительные значения. Вычислить значение переменной 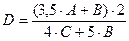и вывести

При А = ___; В = _____; С = ______

D = _____

4. Присвоить переменной А – ваше имя, В – вашу фамилию, Х – год рождения. Вывести следующую информацию:

Фамилия: _______

Имя: _________

Год рождения: _________

Мне ________ лет.

5. Присвоить переменным Х и Y два числа. Вывести:

Для чисел _____ и _____

Сумма = _________

Произведение = _______

Разность = _________

Частное = _________

Линейные задачи

1. Автомобиль на каждом из пяти одинаковых по длине участках дороги шел с известной средней скоростью. Составьте алгоритм и программу для определения средней скорости на всем пути.

2. Вычислить стоимость мебельного гарнитура, содержащего 4 стула, 2 кресла и 1 стол. Стоимость изделий соответственно A, B и C.

3. Напишите программу, запрашивающую ваше имя, фамилию, класс и количество уроков в понедельник, вторник, среду, четверг, пятницу и субботу и выводящую на экран:

Я, <фамилия имя>, ученик <класс> класса.

На этой недели у меня <общее кол-во уроков> уроков.

4. Фруктовый магазин продает яблоки поштучно по 5 руб., груши по 7 руб., апельсины по 8 руб. В первые два дня недели продано: понедельник - Х яблок, Y груш, Z апельсинов; вторник - X яблок, Y груш, Z апельсинов. Напишите программу, которая будет вычислять, на какую сумму продал магазин фруктов в каждый из этих дней и за оба дня вместе.

5. Мальчик, продающий на улице газеты, зарабатывает А руб. на продаже каждой из первых 75 газет. На каждой из остальных проданных газет он зарабатывает по Х руб. Напишите программу, которая выведет заработок мальчика, если он продаст B газет.

6. Мальчик может бегать в три раза быстрее, чем ходить. Скорость его ходьбы равна 4 км/ч. Он принял участие в марафонском забеге, но сошел с дистанции, пробежав только Х км. Сколько времени он потратил на преодоление этого расстояния.

7. Работник зарабатывает Х руб. за каждые 38 часов своей работы. Ему платят в 1,5 раза больше за каждый час сверх 38 часов. Какую сумму он получит, если работает А часов (А должно быть заведомо больше 38).

8. Магазин продает В машин по цене А руб. за каждую. Найти общую выручку от продажи машин.

9. В магазине продается костюмная ткань. Ее цена В руб. за квадратный метр. Напишите программу, которая подсчитает и выведет на экран стоимость куска этой ткани длиной Х метров и шириной 80 см.

10. Хозяин хочет оклеить обоями длинную стену в своем доме. Длина этой стены равна А метров, а высота - В метров. Рулон обоев имеет длину 12 метров и ширину 1м. Сколько будут стоить обои для всей стены, если цена одного руло на К руб.

11. Человеку нужно съездить из Лондона в расположенный в 390 милях Эдинбург. Он может ехать на автомобиле марки Роллс-Ройс, либо на автомобиле марки Форд. Роллс-Ройс расходует 1 галлон бензина на каждые 15 миль пути. Форд расходует 1 галлон бензина на каждые 36 миль пути. Сколько будет стоить поездка в Эдинбург на Ролс-Ройсе, если стоимость 1 галлона бензина составляет Х фунтов? Сколько денег он сбережет, если вместо этого он поедет на машине марки Форд.

12. В видеоигре игрок выигрывает 50 очков, если он сбивает самолет,100 очков, если он сбивает ракету, 200 очков, если он сбивает спутник. Составьте программу, которая выведет на экран число очков игрока, который сбил А самолетов, В ракет и С спутников.

13. Заработок рабочих на фабрике составил С рублей. Его нужно разделить поровну между А рабочими. Выведите заработок каждого рабочего.

14. Составьте алгоритм и программу запроса данных и печати результатов для определения средней экономии горюче-смазочных материалов, если известна средняя экономия в день по бензину, солярке и солидолу.

15. В пяти тестовых опросах мальчик получил оценки. Составьте программу, которая определит среднее значение оценок, полученных мальчиком в пяти опросах.

16. Первая бригада может выполнить задание за А дней, а вторая за В дней. За сколько дней обе бригады выполнят задание, работая вместе.

17. Вводится фамилия ученика, количество занятий (часов) по предмету и количество пропущенных занятий. Вычислить процент посещаемости.

18. Каждую неделю Юра получает деньги на мелкие расходы. Из них он тратит Х рублей на сладости. Это составляет одну четверть того, что он получает еженедельно. Юра сберегает одну треть того, что остается после покупки сладостей. Составьте программу, которая выведет на экран сумму, накопленную Юрой за год.

19. Город А находится от города В на расстоянии S км. Между ними на расстоянии S1 от города А находится город С. Велосипедист выехал из А в В. За какое время он доедет до города В, если до города С он ехал со скоростью V км/ч, от С до В со скоростью V1 км/ч, а в городе С он сделал остановку на 30 мин.

20. Вычислить периметр и площадь прямоугольного треугольника по заданным длинам двух катетов а и b.

21. Заданы координаты трех вершин треугольника (х1, у1), (х2, у2), (х3, у3). Найти его периметр и площадь.

22. Вычислить длину окружности и площадь круга одного и того же заданного радиуса R.

23. Найти произведение цифр заданного четырехзначного числа.

24. Даны два числа. Найти среднее арифметическое кубов этих чисел и среднее геометрическое модулей этих чисел.

25. Дана длина ребра куба. Найти площадь грани, площадь полной поверхности и объем этого куба.

26. Дана сторона равностороннего треугольника. Найти площадь этого треугольника, его высоты, радиусы вписанной и описанной окружностей.

27. Известна длина окружности. Найти площадь круга, ограниченного этой окружностью.

28. Найти площадь кольца, внутренний радиус которого равен г, а внешний — заданному числу R(R> г).

29. Найти площадь равнобедренной трапеции с основаниями а и b и углом X при большем основании а.

30. Найти площадь треугольника, две стороны которого равны а и b, а угол между этими сторонами равен g.

31. Три сопротивления Rv R2., Rs соединены параллельно. Найдите сопротивление соединения.

32. Составить программу для вычисления пути, пройденного лодкой, если ее скорость в стоячей воде V1 км/ч, скорость течения реки V2 км/ч, время движения по озеру t1 ч, а против течения реки — t2 ч.

33. Текущее показание электронных часов: т часов (0 <= т <= 23), п мин (0 <= п <= 59),
к сек (0 <= к <= 59). Какое время будут показывать часы через P часов Q мин R сек?

34. Полторы кошки за полтора часа съедают полторы мышки. Сколько мышек съедят X кошек за Y часов?

35. Дана величина А, выражающая объем информации в байтах. Перевести А в более крупные единицы измерения информации.

36. Смешано V1 литров воды температуры T1 с V2 литрами воды температуры T2. Найти объем и температуру образовавшейся смеси.

37. Бутылка воды стоит 45 копеек. Пустые бутылки сдаются по 20 копеек, и на полученные деньги опять покупается вода. Какое наибольшее количество бутылок воды можно купить, имея некоторую сумму денег S копеек?

38. Определить номера подъезда и этажа по номеру квартиры девятиэтажного дома, считая, что на каждом этаже ровно 4 квартиры, а нумерация квартир начинается с первого подъезда.

39. Дано четырехзначное число. Получить число, записанное теми же цифрами в обратном порядке.

40. Пусть даны четыре целых числа (hour, min, sec, time). Первые три из них (hour, min, sec) — это время запуска ракеты в часах, минутах и секундах, четвертое (time) определяет время полета в секундах. Найти и вывести время возвращения ракеты на землю. Операцию умножения не использовать.

41. В бригаде, работающей на уборке сена, имеется N косилок. Первая из них работала M часов, а каждая следующая на 10 мин. Больше, чем предыдущая. Сколько часов работала вся бригада?

Стандартные функции.

1. Две точки на плоскости заданы своими координатами (x1,y1) и (x2,y2). Вычислить расстояние между этими точками.

2. Вычислить площадь треугольника по формуле Герона.

S= корень(p(p-a)(p-b)(p-c)) , где p=(a+b+c)/2.

3. Дана десятичная дробь. Округлить ее с точностью до двух знаков после десятичной точки.

4. Вычислить периметр прямоугольного треугольника, если заданы длины его катетов.

5. Найти периметр и площадь прямоугольного треугольника, если известны гипотенуза и один из острых углов (угол задан в градусах).

6. По трем оценкам в четверти вывести итоговую оценку (округлить).

7. Чему равна сумма цифр двузначного числа.

8. Найти сумму цифр четырехзначного числа.

9. Напечатать старшую и младшую цифры пятизначного числа.

10. В трехзначном числе выделить число сотен, десятков и единиц. Вывести каждую цифру числа на отдельной строке:

а) начиная с младшей цифры;

б) начиная со старшей цифры.

11. Дано вещественное число. Вывести старшую цифру дробной части этого числа.

12. Дано вещественное число. Вывести целую и дробную части этого числа на разных строках.

13. Идет К-ая секунда суток. Напечатать сколько полных часов, минут и секунд прошло к данному моменту.

14. Сколько досок шириной 10 см. понадобится, чтобы поставить ограду на участок, имеющий форму ромба, с диагоналями А и В (в метрах).

15. Котенок Васька влез на дерево высотой H метров. Какой длины Вам потребуется лестница, чтобы достать Ваську с дерева. Учтите, что вокруг дерева имеется клумба диаметром A метра и цветы на клумбе мять нельзя.

16. Винни-Пух поднялся на шаре на высоту Н метров. Зависнув на этой высоте, был покусан пчелами и упал на землю. Сколько времени он падал? Результат округлить с точностью до одного знака после запятой.

17. Малыш и Карлсон живут в прямоугольной комнате длиной А метров и шириной В метров. Они решили украсить комнату, покрыв ее как можно большим числом квадратных ковриков со стороной С метров, так чтобы коврики не накладывались друг на друга и не разрезались. Какое наибольшее количество ковриков они смогут разместить в своей комнате.

18. Площадка в парке имеет форму треугольника с длинами сторон А, В, С. Надо засеять эту площадку газонной травкой. Сколько потребуется семян, если известно, что 1 кг. семян хватает, чтобы засеять 100 кв.м.

Приемы программирования.

1. Даны две переменные. Требуется поменять их значения.

а) используя вспомогательную переменную;

б) не используя вспомогательную переменную.

2. Даны величины A,B,C,D. Требуется переставить значения величин так:

В должно получить значение А, С значение В, а D значение С.

3. Даны величины A,B,C,D. Требуется переставить значения величин так:

В должно получить значение А, С значение В, D значение С, а А значение D.

4. Дано действительное число x. Не пользуясь никакими другими арифметическими операциями, кроме умножения, сложения и вычитания, вычислить:

2x⁴- 3x³ + 4x² - 5x + 6

Разрешается использовать не более четырех умножений и четырех сложений и вычитаний.

5. Даны действительные числа x, y. Не пользуясь никакими другими арифметическими операциями, кроме умножения, сложения и вычитания, вычислить:

3x² y² - 2x y² - 7x² y - 4y² + 15xy + 2x² - 3x + 10y + 6

Разрешается использовать не более восьми умножений и восьми сложений и вычитаний.

6. Дано действительное число x. Не пользуясь никакими другими арифметическими операциями, кроме умножения, сложения и вычитания, вычислить:

1 - 2x + 3x² + 4x³ 1 + 2x + 3x² + 4x³

Разрешается использовать не более восьми операций.

7. Дано действительное число a. Не пользуясь никакими другими арифметическими операциями, кроме умножения, получить:

a) a⁴ за две операции; ж) a¹³ за пять операций;

б) a⁶ за три операции; з) a¹⁵ за пять операций;

в) a⁷ за четыре операции; и) a²¹ за шесть операций;

г) a⁸ за три операции; к) a²⁸ за шесть операций;

д) a⁹ за четыре операции; л) a⁶⁴ за шесть операций;

е) a¹⁰ за четыре операции.

8. Дано действительное число a. Не пользуясь никакими другими арифметическими операциями, кроме умножения, получить:

a) a³ и а¹⁰ за четыре операции;

б) a⁴ и a²⁰ за пять операций;

в) a⁵ и a¹³ за пять операций;

г) a⁵ и a¹⁹за шесть операций;

д) a², a⁵, a¹⁷ за шесть операций;

е) a⁴, a¹², a²⁸ за шесть операций.

Задачи повышенной трудности. Целочисленная арифметика.

При выполнении задания нельзя использовать условные операторы и операторы цикла; необходимо оставаться в классе целых типов, можно использовать операции целочисленной арифметики MOD, DIV,*,+,-.

1. Ввести с клавиатуры 2 целых числа: m,n>0. Если m делится на n или n делится на m, то вывести 1, иначе - любое другое число.

2. Ввести с клавиатуры 2 целых числа: m,n>0. Если m<=n, то вывести 1, иначе - любое другое число.

3. Если в четырехзначном числе, введенном с клавиатуры, есть одинаковые цифры, то вывести 1, в противном случаe - любое другое число.

4. Если четырехзначное число, введенное с клавиатуры, является симметричным(например, 1331, 0550), то вывести 1, иначе - любое другое число.

5. Ввести с клавиатуры 4 целых числа: m,n,k,p>0. Если остаток от деления m на n равен k или p, то вывести 1, иначе - любое другое число.

6. Часовая стрелка образует угол alfa с лучом, походящим через центр циферблата и точку, соответствующую 12 часам на циферблате, 0<=alfa<=360.

Ввести с клавиатуры значение alfa и определить значение угла для минутной стрелки, а также количество часов и полных минут, соответствующих данному положению часовой стрелки.

7. Если в четырехзначном числе, введенном с клавиатуры, ровно 3 одинаковых цифры, то вывести 1, иначе - любое другое число.

8. Ввести с клавиатуры два числа и распечатать их в порядке возрастания.

9. Обозначим дни недели цифрами от 1 (понедельник) до 7 (воскресенье) соответственно. Ввести с клавиатуры 2 целых числа 1<=n<=31 (число в текущем месяце), 1<=m<=7 (день недели первого числа текущего месяца). Определить, на какой день недели приходится число n.

10. Ввести с клавиатуры 2 целых числа: 0<=m<=60, 0<=h<=12, описывающие момент времени "h часов m минут". Определить наименьшее число полных минут, которое должно пройти до того момента, когда часовая и минутная стрелки на циферблате совпадут на каком-либо делении.

11. Ввести с клавиатуры 2 целых числа: 0<=m<=60, 0<=h<=12, описывающие момент времени "h часов m минут". Определить наименьшее число полных минут, которое должно пройти до того момента, когда часовая и минутная стрелки на циферблате расположатся перпендикулярно друг к другу.

12. По введенному вещественному числу x вывести целочисленное значение функции sign(x).

13. Текущее показание электронных часов m часов( 0<=m<=23), n минут (0<=n<=59), k секунд (0<=k<=59). Какое время будут показывать часы через p часов q минут r секунд?

Логический тип данных

1. Вычислить значение выражений.

При a = 10, b = 20, c = true, d= false

a) (a>5) and (b>5) and (a<20) and (b<30)

b) not(a<15) or not (b<30)

c) c or d and (b=20)

d) k mod 7 = k div 5 – 1 при k=15

e) odd (trunс (10*p)) при p = 0.182

f) not odd (n) при n = 0

g) false < true

h) pred (true)

i) (p<true) = (q = false) при p=q=true

j) ord (succ (false)) >0

k) not (pred(c) or (ord (c) = 1))) при c=true

l) a and b > a or b при a=false, b= true

2. Вычислить значения выражений:

1) a or b and not a при a=true, b=false;

2) not a and b при a=true, b=false;

3) (p<true)=(q=false) при p, q=true.

4) a or (not b) при a=false, b=true.

5) a and b>a or b при a=false, b=true;

6) (a or b) and not a при a=true и b=false;

7) not (a and b) при a=true и b=false.

3. Указать порядок выполнения операций при вычислении выражения (надписав над знаком операции номер действия):

1) (x>=0) or t and z or (y*y<>4) 2) a and b or not c and d

4. Доказать тождества:

1) a or (not a)=true; 6) a and (b or c)=(a and b) or (a and c);

2) a and (not a)=false; 7) a and b=(a<true)<b;

3) false and a =false; 8) not (not a)=a;

4) true or a =true 9) a<=b=not a or b;

5) a or a=a; 10) not(a or b)=(not a) and (not b);

5. Объяснить ошибки в следующих записях:

1) true + false; 3) not 2=5; 5) x>0 or y=4.

2) 1 and 0; 4) true<0; 6) not not b or or d.

6. Записать на Паскале выражение, истинное при выполнении указанного условия и ложное в противном случае:

a) 0<X<1

b) X=MAX(x,y,z)

c) X< >MAX(x,y,z)

d) хотя бы одна логическая переменная А и В имеют значение true

e) обе логические переменные А и В имеют значение true

f) x принадлежит [2,5] или [-1,1]

g) x лежит вне отрезков [2,5] и [-1,1]

h) y — номер года. Является ли год високосным. (Год високосный, если он делится на 400 или делится на 4 , но не делится на 100)

i) целые N и К имеют одинаковую четность

j) только одна из логических переменных А и В имеют значение True

k) a, b, c — стороны треугольника. Записать, что треугольник существует.

l) три целых числа n, k, m имеют одинаковую четность

7. Составить программу, печатающую значение true, если указанное высказывание является истинным, и false в противном случае:

a) сумма двух первых цифр заданного четырехзначного числа A равна сумме двух его последних цифр;

b) сумма цифр данного двузначного числа N является четным числом;

c) точка с координатами (х, у) принадлежит части плоскости, лежащей между прямыми
х =m, х = n (m < n);

d) квадрат заданного трехзначного числа равен кубу суммы цифр этого числа;

e) целое число N является четным двузначным числом;

f) треугольник со сторонами а, b, с является равносторонним;

g) треугольник со сторонами а, b, с является равнобедренным;

h) среди чисел а, b, с есть хотя бы одна пара взаимно противоположных чисел;

i) числа с и b выражают длины катетов одного прямоугольного треугольника, а с и d — другого. Эти треугольники являются подобными;

j) даны три стороны одного и три стороны другого треугольника. Эти треугольники равновеликие, т.е. имеют равные площади;

k) данная тройка натуральных чисел а, b, с является тройкой Пифагора, т.е. с2 = а2 + b2;

l) все цифры данного четырехзначного числа N различны;

m) данные числа х, у являются координатами точки, лежащей в первой координатной четверти;

n) (x1, у1) и (х2, у2) — координаты левой верхней и правой нижней вершин прямоугольника; точка А(х, у) лежит внутри этого прямоугольника или на одной из его сторон;

o) число с является средним арифметическим чисел а и b;

p) натуральное число N является точным квадратом;

q) цифры данного четырехзначного числа N образуют строго возрастающую последовательность;

r) цифры данного трехзначного числа N являются членами арифметической прогрессии;

s) цифры данного трехзначного числа N являются членами геометрической прогрессии;

t) данные числа c и d являются соответственно квадратом и кубом числа а;

u) цифра М входит в десятичную запись четырехзначного числа N;

v) данное четырехзначное число читается одинаково слева направо и справа налево;

w) сумма двух натуральных чисел кратна 2;

x) произведение натуральных чисел а и b кратно числу с;

y) сумма двух действительных чисел а и b является целым числом, т.е. дробная часть суммы равна нулю;

z) данное натуральное число а кратно числу b, но не кратно числу с.

8. Переменной T присвоить значение выражения, истинного при выполнении указанного условия и ложного в противном случае:

1) логические переменные a и b имеют одинаковые значения;

2) целое число n кратно 4;

3) хотя бы одна из логических переменных a и b имеет значение true;

4) целое n и k имеют одинаковую четность;

5) целое число а - четное;

6) только одна из логических переменных a и b имеет значение true;

7) ни одна из логических переменных a, b, c не имеет значения true;

8) точка с координатами (x, y) принадлежит отрезку [a, b].

9) точка (x, y) лежит вне отрезка [a, b].

10) точка (x, y) принадлежит интервалу (а, b) или (с, d).

11) точка (x, y) лежит вне отрезков [-5,5] и [ 10,15].

12) точка (x, y) лежит вне круга радиусом r с центром в точке (0,0);

13) не существует треугольника с длинами сторон a, b, c.

9. Переменной Т присвоить значение True, если первая дата предшествует второй (в пределах одного года), и значение False в противном случае. Задать d1,m1 - день и месяц первой даты, d2,m2 - вторая дата.

10. Если поля шахматной доски (d1,v1) и (g2,v2) имеют одинаковый цвет, вывести True, в противном случае False. Здесь g1,v1,g2,v2 - целые числа в диапазоне от 1 до 8.

11. Если ферзь, расположенный на поле (g1,v1), бьет поле (g2,v2) шахматной доски, то вывести True, в противном случае False. Здесь g1,v1, g2,v2 - целые числа в диапазоне от 1 до 8.

Алгоритмы ветвления.

Дата добавления: 2018-11-24; просмотров: 563; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 4 5 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!