Пример решения задачи о распределении тепла в пластине
Лабораторная работа № 7. Использование MATLAB для решения уравнений в частных производных
Введение
Система MATLAB оснащена разнообразными библиотеками функций, специализированных для решения задач из различных областей математики, физики, механики и других научных направлений. Эти библиотеки в английских названиях содержат слово ToolBox, что в переводе означает «ящик инструментов».
Предусмотрен ToolBox для численного решения краевых задач уравнений математической физики, области определения которых двумерные, т.е. лежат в плоскости, параметризованной двумя декартовыми координатами x и y. Он имеет название PDE ToolBox, образованное от слов Partial Differential Equations (уравнения в частных производных).
Дифференциальные уравнения, определяющие искомые решения в заданной области G, содержат частные производные по x и y различных порядков, и поэтому называются уравнениями в частных производных. Уравнения статических задач содержат только пространственные производные и во многих случаях относятся к классу эллиптических уравнений в соответствии с принятой в математике классификацией. Такие уравнения дополняются краевыми условиями на границе области определения, которые дают однозначность решения задачи.
В динамических задачах в качестве независимой переменной присутствует время, и в уравнениях содержатся также частные производные искомых решений по времени. Для однозначности решения в этом случае дополнительно к граничным условиям должны задаваться начальные условия.
|
|
|
PDE ToolBox позволяет решать уравнения и системы уравнений в общей постановке, но для специализированных типов задач предусмотрена возможность упрощенного задания исходных данных посредством специальных интерфейсов.
Из их числа применительно к исследованиям прочностных свойств изделий представляют интерес два класса задач:
- задача расчета температурного поля в пластине из проводящего тепло материала при действии тепловых нагрузок,
- задача расчета плоского напряженного состояния пластинки под действием внешних нагрузок.
Дифференциальные уравнения для этих задач в статической постановке относятся к классу эллиптических. Динамические уравнения первого из этих классов являются гиперболическими, а второго – гиперболическими.
В данной работе рассмотрена задача расчета статического температурного поля в пластине.
Графическая среда PDE ToolBox
С помощью PDE ToolBox могут быть решены двумерные уравнения математической физикис применением метода конечных элементов. Вызов графической среды PDE ToolBox выполняется командой pdetool или pdeinit (см. рис. 1).
|
|
|
Можно выделить следующие этапы решения уравнений в частных производных:
1. Конструирование (построение) области, в которой решается уравнение.
2. Ввод уравнения в частных производных.
3. Определение начальных и граничных условий.
4. Триангуляция области.
5. Решение уравнения.
6. Визуализация результата.
 |  |
|
|
Рис. 1 Графическая среда PDE ToolBox
Пример решения задачи о распределении тепла в пластине
Уравнение распространения тепла в пространственной области V имеет вид:
(1)
где u – температурное поле в области V,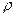 
- плотность теплопроводящей среды, c – теплоемкость, 
- коэффициент теплопроводности. В случае однородной изотропной среды уравнение (1) можно переписать в виде
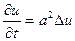(2)
где 
- коэффициент температуропроводности, 
- оператор Лапласа.
На части границы области V могут быть заданы условия Дирихле (заданная величина температуры)
|
|
|
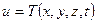(3)
а на остальной части условия Неймана
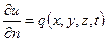(4)
где q – тепловой поток, проходящий внутрь области V, n – внешняя нормаль к ее границе.
В PDE ToolBox решается двумерная задача, которая может применяться, например, к пластинке постоянной толщины, теплоизолированной по обеим сторонам, а теплообмен осуществляется через боковые границы.
Задача состоит в том, чтобы найти статическое распределение тепла в области G, изображенной на рис. 2.
Круговые отверстия имеют одинаковый размер диаметра - 0.6 м. Правая и левая границы теплоизолированы. Коэффициент теплопроводности = 225.
Дифференциальное уравнение, описывающее распределение температуры, записывается в виде уравнения Пуассона:
(5)
Условия на левой и правой границах области G имеют вид, соответствующий теплоизоляции:
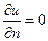(6)
Здесь n - вектор нормали к границе.
На верхней и нижней границах области G поддерживается температура равная 580 градусов, поэтому там
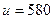(7a)
|
|
|
На окружностях поддерживается температура равная 450 градусов, поэтому там
(7b)
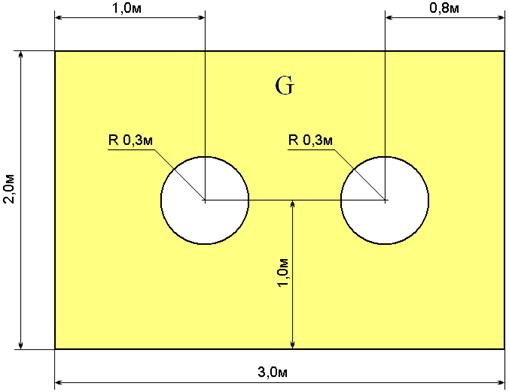
Рис. 2 Область G
Таким образом, задача о распределении тепла в области G полностью описывается уравнением (5) и граничными условиями.
Рассмотрим подробно процесс решения этой задачи в PDE ToolBox. Первый этап - конструирование области. Запустив среду PDE ToolBox (см. рис. 1), вы увидите, что по умолчанию область решения задачи должна лежать в прямоугольнике [-1.5 1.5; -1 1]. Необходимо установить другие границы изменения х и у (в рассматриваемом случае можно установить границы изменения х от -1 до 4, у - от -1 до 3). Для изменения границ отображаемой области по x и y необходимо выполнить команду меню Options ► Axes Limits (Настройки ► Пределы осей), после чего появится окно, в котором указаны границы изменения х и у (рис. 3). Изменим границы х (от -1 до 4) и у (от -1 до 3) (рис. 4).
Рис. 3 Окно Axes Limits Рис. 4 Новые значения границ
Для удобства можно изобразить линии сетки на координатной сетке. Для этого необходимо выполнить команду меню Options ► Grid (Настройки ► Сетка), после чего среда PDE ToolBox будет иметь вид, изображенный на рис. 5.
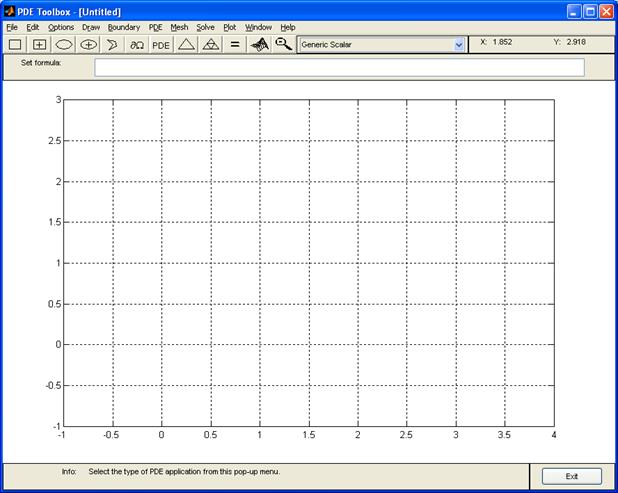
Рис. 5 Область G
Для конструирования области (в которой решается уравнение) предназначен пункт меню Draw (Рисовать). Для перехода в режим конструирования можно выполнить команду меню Draw ► Draw Mode (Рисовать ► Режим рисования) или просто выбрать один из геометрических примитивов и начать рисовать. Геометрические примитивы можно выбирать в пункте меню Draw или воспользоваться панелью рисования области. В PDE ToolBox есть следующие примитивы для рисования области:
Ø прямоугольник. Для выбора прямоугольника можно выполнить команду меню Draw ► Rectangle/ s quare (Рисовать ► Прямоугольник/квадрат) или щелкнуть по кнопке 
на панели рисования области; если при прорисовке фигуры удерживать клавишу Ctrl, то вместо прямоугольника получится квадрат;
Ø центрированный прямоугольник. Для выбора этой фигуры можно выполнить команду меню Draw ► Rectangle/ s quare (centered) (Рисовать ► Прямоугольник/квадрат (Центрированный)) или щелкнуть по кнопке 
на панели рисования области; если удерживать клавишу Ctrl, то вместо прямоугольника получится квадрат. Отличие этого прямоугольника от обычного состоит в том, что при прорисовке прямоугольник растягивается не только в сторону правого нижнего угла, но и левого верхнего;
Ø эллипс. Для его выбора можно выполнить команду Draw ► Ellipse/ c ircle (Рисовать ► Эллипс/круг) или выбрать инструмент 
на панели рисования области), при нажатой клавише Ctrl вместо эллипса получится круг; кроме обычного эллипса есть центрированный (команда меню Draw ► Ellipse/ c ircle (centered) (Рисовать ► Эллипс/круг (Центрированный)) или кнопка 
;
Ø многоугольник (команда меню Draw ► Polygon (Рисование ► Многоугольник) иди кнопка 
).
Построенные объекты можно поворачивать с помощью команды Draw ► Rotate… (Рисование ► Повернуть…).
Для решения рассматриваемой задачи необходимо нарисовать прямоугольник, а в нем два круга. Начав с рисования прямоугольника, следует нарисовать его по возможности точнее. Для уточнения координат прямоугольника необходимо дважды щелкнуть по прямоугольнику, что приведет к появлению диалогового окна Object Dialog (Вызов диалогового окна для изменения свойств объекта) - рис. 6.
Рис. 6 Диалоговое окно Object Dialog
Параметры Left (Левый) и Bottom (Нижний) определяют координаты левого нижнего угла прямоугольника, там следует ввести нули (левый нижний угол в данном случае совпадает с началом координат). Параметры Width (Ширина) и Height (Высота) определяют ширину и высоту прямоугольника (для решаемой задачи эти величины равны 3 и 2 соответственно). Параметр Name (Имя) определяет имя объекта. Все прямоугольники по умолчанию начинаются с «R» (от английского слова Rectangle), имя эллипса начинается с буквы «Е», круга - с буквы «С», многоугольника - с буквы «P», квадрата - с букв «SQ».
Следующим этапом будет рисование двух кругов, первый - с центром в точке (1, 1) и радиусом 0.3, второй - с центром в точке (2.2, 1) и радиусом 0.3. Для построения круга используется кнопка 
при нажатой клавише Ctrl. Затем следует уточнить его координаты: X-Center, Y-Center - координаты центра круга, Radius - радиус круга (рис. 7).
Рис. 7 Диалоговое окно Object Dialog для круга
Рис. 8 Диалоговое окно Object Dialog для круга
Теперь надо определить способ построения области G при помощи операций над множествами точек построенных элементарных объектов. Для этого в PDE ToolBox имеются операции:
- - операция вычитания объектов, имеет наивысший приоритет;
+ - операция объединения объектов;
* - операция пересечения объектов.
Операции пересечения и объединения имеют одинаковый приоритет. Для изменения приоритетов, как и в алгебре, могут использоваться круглые скобки.
По умолчанию созданные объекты соединяются с помощью знака «плюс». В рассматриваемом случае необходимо из прямоугольника вычесть два круга, поэтому в области формулы необходимо исправить формулу на R1-C1-C2 (рис. 8).
Рис. 9 Выбор типа решаемой задачи
Рис. 10 Окно PDE Specification - определение типа и коэффициентов дифференциального уравнения в частных производных
На втором этапе решения задачи необходимо ввести уравнение в частных производных. В PDE ToolBox есть возможность задавать тип решаемой задачи. Для этого можно воспользоваться командой Options ► Application (Настройки ► Приложение) - рис. 9 или раскрывающимся списком 
. Для ввода уравнений служит пункт меню PDE. Первый подпункт этого меню PDE Mode служит для перехода в режим ввода уравнений. Второй подпункт служит для показа подобластей, входящих в область решения. В решаемой задаче есть всего одна подобласть. Третий пункт PDE Specification или кнопка 
позволяет выбрать тип уравнений и ввести его коэффициенты (рис. 10).
При решении данной задачи следует выбрать в качестве типа задачи Heat Transfer (Задача о распределении тепла) или просто ввести коэффициенты эллиптического уравнения в окне PDE Specification. Установив тип решаемой задачи Heat Transfer, параметры уравнения в частных производных следует определить в окне PDE Specification (рис. 11).
Заметим здесь, что для скалярной функции Т(х, у, z) ee градиентом является вектор grad(T), компоненты которого равны 
, а дивергенция от градиента div(grad(T)) вычисляется по формуле: 
(в плоской задаче координата z отсутствует).
Рис. 11 Окно PDE Specification - определение коэффициентов задачи о распределении тепла
Третий этап решения задачи посвящен определению граничных условий. Для ввода граничных условий предназначен пункт меню Boundary (Граничные условия). Для перехода в режим ввода граничных условий можно выполнить команду меню Boundary ► Boundary Mode (Граничные условия ► Режим граничных условий) или воспользоваться кнопкой 
или же комбинацией клавиш Ctrl+B.
После этого, чтобы определить граничные условия, необходимо щелчком мыши выделить границу и выполнить команду меню Boundary ► Specify Boundary Condition (Граничные условия ► Установить граничные условия) или осуществить двойной щелчок мышью по выделенной границе. (Если необходимо объединить несколько участков границы, то в этом случае щелчок по каждому из участков осуществляется при нажатой клавише Shift).
На верхнем и нижнем участках границы области определены условия Дирихле вида
hT = r ,
и в окне Boundary Condition следует ввести h = 1, r = 580 (рис. 12).
Рис. 12 Ввод условий для верхней и нижней границ области G
Выделив одновременно контуры отверстий, установить температуру 450 градусов (рис. 13).
Рис. 13 Ввод условий на границах отверстий области G
Рис. 14 Ввод условий Неймана для левой и правой границы области G
Осталось ввести условия Неймана вида (6) (или, что то же самое, n • k • grad(T) = 0) на левой и правой границе области G (рис. 14).
Ввод условий задачи завершен.
На четвертом этапе выполнить триангуляцию области - покрыть область сеткой, состоящей из треугольников. Это и есть конечные элементы, на которые разбивается область. Режимом триангуляции управляет пункт меню Mesh (Сетка). Для перехода в режим триангуляции служит команда Mesh ► Mesh Mode (Сетка ► Режим сетки). Переход в режим триангуляции сразу разбивает на крупные треугольники (рис. 15). Этого же можно добиться с помощью команды начала триангуляции - пункт меню Mesh ► Initialize Mesh (Сетка ► Определить (Инициализировать) сетку), комбинация клавиш Ctrl + I или кнопка 
.
Обычно начальной триангуляции недостаточно для получения решения с удовлетворительной точностью. Для разбиения области на более мелкие треугольники служит команда меню Mesh ► Refine Mesh (Сетка ► Улучшить сетку) или кнопка 
. Для решаемой задачи критерием достаточной величины треугольников может служить вид отверстий. Двойное применение команды Mesh ► Refine Mesh, дает сетку, необходимую для получения решения с достаточной точностью (рис. 16). Следует учесть, что из-за слишком мелкой сетки время решения задачи значительно увеличивается. Возврат к начальной триангуляции осуществляется с помощью команды меню Mesh ► Initialize Mesh или кнопки .
Рис. 15 Начальная триангуляция области G
На пятом этапе для решения поставленной задачи необходимо выполнить команду меню Solve ► Solve PDE (Решение ► Решить PDE) или щелкнуть по кнопке 
. После этого найденное решение автоматически изображается на экране в виде цветного контурного графика (рис. 17).
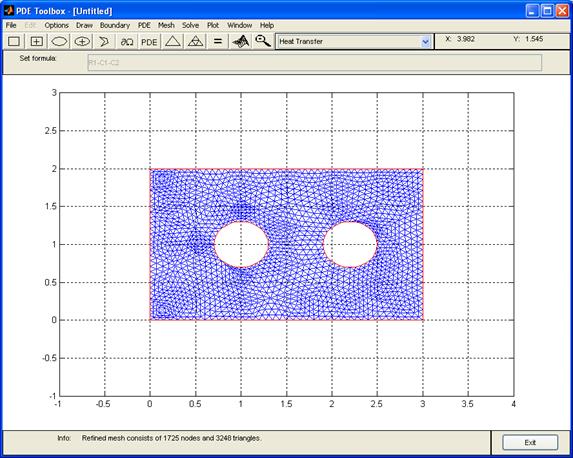
Рис. 16 Уменьшенная сетка в области решения G
Шестой этап решения задачи состоит в обработке графического представления результатов.
Контурный график не всегда достаточно хорошо позволяет проанализировать полученное решение. Пользователь может изменить тип построенного графика, для чего можно выполнить команду меню Plot ► Parameters (График ► Параметры) или щелкнуть по кнопке 
. В появившемся диалоговом окне (рис. 18) можно установить необходимые параметры графика решения, для построения трехмерного графика достаточно установить флажок Height (3-D plot). На рис. 19 изображен трехмерный график найденного решения задачи.
Рис. 17 Контурный график решения задачи
Рис. 18 Диалоговое окно для установки параметров графика
Рис. 19 Трехмерный график решения задачи
При решении задачи были рассмотрены основные этапы решения дифференциального уравнения в частных производных в графической среде PDE ToolBox.
Теперь рассмотрим, как в PDE ToolBox хранится область решения, сетка и полученное решение. Для экспорта области решения в меню Draw есть команда Export Geometry Description, Set Formula, Labels… (Экспорт описания геометрии области, формулы, меток), с помощью которой (рис. 20) можно экспортировать геометрию области и формулу связи между объектами в MATLAB.
Рис. 20 Диалоговое окно Export, функция Export Geometry Description, Set Formula, Labels...
Как видно из рис. 20, можно экспортировать три объекта gd, sf и ns. Матрица геометрии области хранится в gd, формула связи хранится между объектами в переменной sf. Рассмотрим структуру матрицы gd на примере области G (рис. 8.29).
gd =
3.0000 1.0000 1.0000
4.0000 1.0000 2.2000
0 1.0000 1.0000
3.0000 0.3000 0.3000
3.0000 0 0
0 0 0
0 0 0
0 0 0
2.0000 0 0
2.0000 0 0
Число столбцов матрицы совпадает с количеством объектов, входящих в область решения, каждый столбец отвечает за отдельный объект. Рассмотрим структуру каждого столбца. Первый элемент столбца содержит номер объекта: 1 - круг, 2 - многоугольник, 3 - прямоугольник, 4 - эллипс.
Для прямоугольника и многоугольника второй элемент столбца содержит количество сторон фигуры, далее хранятся координаты вершин.
Для круга второй и третий элементы содержат координаты центра круга, четвертый - радиус.
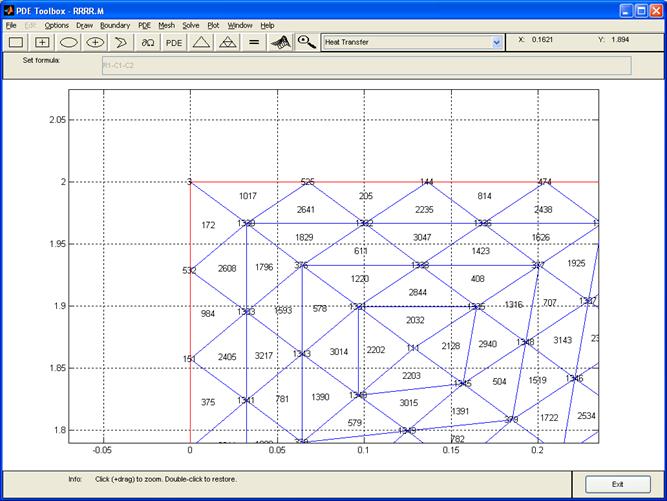
Рис. 21 Сетка с пронумерованными узлами и конечными элементами
Эллипс отличается от круга тем, что четвертый и пятый элементы столбца содержат величины полуосей эллипса, а шестой - угол поворота в радианах. В текстовой переменной sf хранится формула:
sf =
R1-C1-C2
Для вывода на экран номеров узлов сетки служит команда Mesh ► Show Node Labels (Сетка ► Показать узлы сетки), а для вывода номеров треугольных конечных элементов - команда Mesh ► Show Triangle Labels (Сетка ► Показать метки треугольных элементов). После нумерации узлов и конечных элементов сетка будет иметь вид, такой как на рис. 21 (Показан фрагмент сетки, выделенный при помощи кнопки 
).
Теперь рассмотрим, как хранится сетка. Для этого экспортируем ее в MATLAB с помощью пункта меню Mesh ► Export Mesh (Сетка ► Экспорт сетки) - рис. 22.
Рис. 22 Окно Export, функция Export Mesh
Матрица p содержит координаты всех точек, каждый столбец содержит координаты одной точки (координаты х и у); для области G она имеет вид (фрагмент в редакторе матриц):
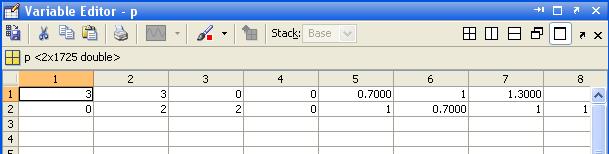
Матрица t содержит 4 строки:
В каждом столбце матрицы: первые три элемента содержат номера узлов, образующих треугольник (конечный элемент), четвертый - номер подобласти, которой он принадлежит. Число столбцов матрицы t равно количеству конечных элементов, на которые разделена область, Для области G матрица t будет такой (4-я строка постоянно равна 1, так как область решения состоит из одной подобласти):
В матрице е находится информация об узлах, формирующих границу подобласти. В нашем примере матрица е имеет вид:
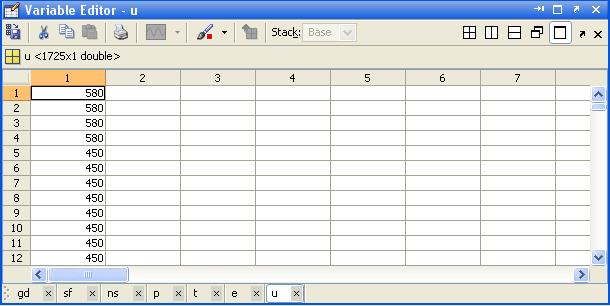
Решение представляет собой массив значений u: его элементы соответствуют координатам узлов, определенных матрицей р. Количество элементов массива решений u равно количеству столбцов матрицы р. Для экспорта решения в MATLAB служит команда меню Solve ► Export Solution (Решение ► Экспорт решения). Сопоставляя значения матриц р, t и е, можно анализировать полученное решение в различных точках. Чем мельче сетка, тем более точное решение будет получено. Но, с другой стороны, мелкая сетка требует больше времени решения задачи.
Дата добавления: 2018-11-24; просмотров: 1699; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!