Динамика колебаний пружинного маятника.

Стр 1 из 2Следующая ⇒

Министерство образования Республики Беларусь Учреждение образования Международный государственный экологический университет им. А.Д. Сахарова Факультет мониторинга окружающей среды Кафедра физики и высшей математики

Лабораторная работа № 7

ИЗУЧЕНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ

ПРУЖИННОГО МАЯТНИКА

Минск

2013

ИЗУЧЕНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ ПРУЖИННОГО МАЯТНИКА

Цель работы: определить коэффициенты жёсткости пружин маятника, определить массу неизвестного груза с помощью пружинного маятника.

Приборы и оборудование: набор пружин, набор грузов, штатив, секундомер, электронные весы.

Теоретическая часть

Колебания

Колебаниями называются процессы, в той или иной степени повторяющиеся во времени.

Если мы говорим, что система колеблется, то под этим подразумевается, что некоторая физическая величина, характеризующая систему, совершает колебания, т. е. изменяется, неоднократно принимая одно и то же значение.

Свободными колебаниями (или собственными)называются колебания, происходящие в системе, предоставленной самой себе в отсутствие внешних воздействий. Такие колебания возникают в системе в результате однократного выведения ее из состояния устойчивого равновесия. При свободных колебаниях в системе всегда действуют силы (в общем случае причины), стремящиеся возвратить систему в положение равновесия (положение, при котором в системе отсутствуют колебания). В случае колебаний груза на пружине возвращающей силой будет сила упругости пружины. Частота, с которой происходят собственные колебания, называется собственной частотой колебаний.

Вынужденными колебаниями называют колебания системы, вызванные действием на нее внешней периодической силы (внешнее периодическое воздействие), называемое вынуждающей силой. Если подвешенный на пружине груз двигать рукой вверх-вниз с некоторой частотой, то роль вынуждающей силы выполняет сила, действующая на груз со стороны руки.

Интересно, что при некотором значении (или даже значениях) частоты внешнего воздействия, называемой резонансной частотой, наступает резонанс – резкое возрастание амплитуды установившихся вынужденных колебаний. Резонанс наступает при частоте внешнего воздействия, близкой к собственной.

Периодические колебания

Колебания некоторой физической величины S называются периодическими, если все значения этой величины полностью повторяются через одно и то же время Τ , называемое периодом, т. е. S ( t + Τ) = S ( t ) для любого значения времени t . Если Τ – период, то 2Т, 3Т , 4Τ ,... тоже периоды. Поэтому в физике под периодом обычно понимают наименьший период, т. е. наименьший отрезок времени, через который физическая величина S повторяется. При этом говорят, что за время одного периода совершается одно колебание.

Частотой периодических колебаний ν называется число колебаний в единицу времени. Легко показать, что

Действительно, если за время t совершено N колебаний, то частота , а период . Отсюда видно, что . В системе СИ единицей измерения частоты служит Герц (Гц), 1 Гц = с^-1.

Пусть периодически колеблющаяся величина S изменяется в пределах от S₀– А до S₀+ А, где А > 0. Тогда говорят, что величина S колеблется с амплитудой А около значения S ₀ . Размах колебаний (разница между двумя крайними положениями) равен 2А.

Гармонические колебания

Важным частным случаем периодических колебаний являются гармонические колебания, т. е. такие изменения во времени t физической величины S , которые идут по закону

, (1)

где А > 0, ω > 0. Из курса математики известно, что функция вида (1) меняется в пределах от – А до А , и что наименьший положительный период у нее . Поэтому гармоническое колебание вида (1) происходит с амплитудой А и периодом .

Не следует путать циклическую (круговую) частоту ω ичастоту ν колебаний.

Между ними простая связь. Так как и , то

В системе СИ размерность как ω, такиν равна с^-1. Наименование Гц обычно применяется только для величины ν , а если необходимо указать размерность ω, то пишут просто с^-1.

Величина называется фазой колебаний. Фаза растет пропорционально времени. При t = 0 фаза равна , и поэтому называется начальной фазой. Она зависит от отклонения и скорости в момент начала отсчета времени.

Отметим, что при одном и том же t: , где n=0, ±1, ±2, … Видно, что начальная фаза для одного и того же колебания есть величина, определенная с точностью до 2π n . Поэтому из множества возможных значений начальной фазы выбирают, обычно, модуль ее наименьшего значения.

Иногда полезно знать характер изменения первой и второй производных по времени от величины S , которая совершает гармонические колебания (колебания по гармоническому закону). Если , то дифференцирование S по времени t дает

, .

С учетом (1) получаем, что , т.е.

. (2)

Равенство (2) называют дифференциальным уравнением гармонических колебаний.

Таким образом, мы получили чрезвычайно важное утверждение:

если используя законы физики для физической величины S удалось записать дифференциальное уравнение вида , то отсюда будет следовать, что S изменяется обязательно, по гармоническому закону с циклической частотой ( 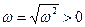). Конкретные значения амплитуды А и начальной фазы зависят от начальных условий.

Заметим, что в (2) стоит величина , которая всегда положительна. Поэтому, например, уравнение не будет дифференциальным уравнением гармонических колебаний, т.к. не найдется такого действительного значения , для которого было бы равно « – 6 ».

Динамика колебаний пружинного маятника.

Маятниками называются протяженные тела различной формы и размеров, совершающие колебания около точки подвеса или опоры. При отклонении из положения равновесия сила тяжести и упругие силы определяют в каждый момент времени ускорение маятника, т. е. определяют характер его движения (колебания). Рассмотрим динамику колебаний на простейшем примере пружинного маятника.

Пусть на гладком горизонтальном столе груз массой m совершает колебания вдоль оси x на легкой пружине жесткости k(рис. 5), прикрепленной одним концом к грузу, а другим к стене. Покажем, что свободные колебания такого пружинного маятника гармонические и найдем их период.

Начало координат (x = 0) поместим в точку, соответствующую равновесному положению груза. За колеблющуюся физическую величину возьмем координату груза.

1-й способ решения. Используется второй закон Ньютона.

Пусть груз при колебаниях в некоторый момент времени t имеет координату x = x ( t ). Тогда проекция на ось x силы , действующей на груз со стороны пружины,

(3)

при любом знаке x , что легко проверить. На рис. 5 покачано направление силы при x > 0. На груз еще действует сила тяжести и сила нормального давления со стороны стола. По второму закону Ньютона

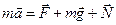где – ускорение груза.

Это векторное равенство, записанное в проекциях на ось x, имеет вид

ma_x = F_x.

Здесь а_х = х" – проекция на ось x ускорения. Учитывая (4), имеем

т х"= - k х. Отсюда

Последнее уравнение есть дифференциальное уравнение гармонических колебаний с циклической частотой и периодом

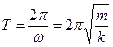(4).

2-й способ. Используется закон сохранения энергии.

В момент, когда груз имеет координату x и проекцию на ось x скорости x ', кинетическая энергия груза будет , а потенциальная энергия деформированной пружины . Так как полная энергия системы при колебаниях сохраняется, то

Продифференцируем последнее равенство по времени:

. Откуда следует .

Как и в первом способе решения, но уже другим путем, мы получили дифференциальное уравнение гармонических колебаний с циклической частотой
и периодом

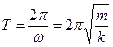(4).

Главной особенностью движения рассмотренного маятника является независимость амплитуды колебаний от частоты. Это справедливо при небольшой амплитуде, когда величина деформации пружины пропорциональна силе, действующей на пружину (см.(4)). При большой амплитуде колебаний это условие нарушается, и частота колебаний начинает зависеть от амплитуды.

Уравнение колебаний пружинного маятника:

. (5)

Амплитуду колебаний А и начальную фазу φ₀ можно определить, зная положение груза x ₀ и его скорость v ₀в некоторый момент времени, например, t = 0.

Продифференцируем уравнение (5) по времени:

. (6)

Подставив в (5) и (6) значения координаты и скорости груза при , получим систему уравнений

, (7)

из которой легко найти А и φ₀:

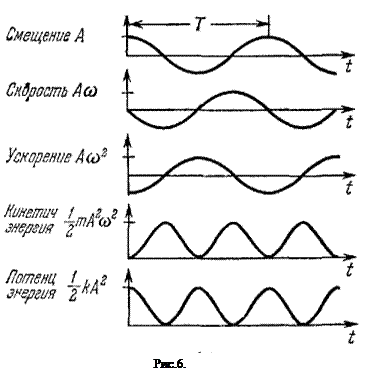
При гармонических колебаниях полная энергия остается постоянной, но кинетическая и потенциальная, каждая в отдельности, совершают колебания во времени. В момент, когда колеблющееся тело достигает крайнего положения и имеет скорость, равную нулю, вся энергия является потенциальной – кинетическая равна нулю. Когда тело проходит через положение равновесия, вся энергия является кинетической – потенциальная равна нулю (если в положении равновесия потенциальная энергия равна нулю). Поскольку тело за период колебаний два раза проходит через положение равновесия, то частота колебаний кинетической энергии в два раза больше частоты колебаний груза. С таким же периодом колеблется и потенциальная энергия.

На рис.6 показан ход изменения со временем величин, характеризующих движение маятника.

Если в некоторой системе, не обязательно состоящей из груза и пружины, возвращающая сила пропорциональна отклонению от положения равновесия, то такая система становится подобной пружинному маятнику, и в ней могут возникнуть гармонические колебания.

Практическая часть

I. Определение коэффициента жёсткости пружины пружинного маятника.

1. Ознакомьтесь с экспериментальной установкой (рис.7) и правилами работы с секундомером.

2. Определите время своей реакции. Для этого быстро включите и выключите секундомер. Полученное значение используйте в качестве систематической погрешности измерения времени.

3. Подвесьте на пружине груз известной массы.

4. Вызовите вертикальные колебания груза небольшой амплитуды (2 – 3 см).

5. Измерьте время, за которое груз совершает 40 колебаний.

6. Опыт повторите 6 раз. Данные занесите в таблицу 1.

7. Определите период колебаний груза 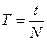, его среднее значение. Данные занесите в таблицу 1.

8. Рассчитайте погрешность периода с учетом случайной и систематической погрешностей.

9. Запишите полученный результат

10.Определите, используя формулу (5), жёсткость пружины . Определите погрешность в определении . Запишите полученный результат измерений.

11. Замените пружину, проделайте со второй пружиной те же опыты что и п.п. 3-10.

Таблица 1

	№	N	t_i, c	T_i, c	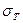, c	, c
1 пружина	1
	2
	3
	4
	5
	6
2 пружина	1
	2
	3
	4
	5
	6

12.Сравните полученные и .

13. Измерьте длину пружин и , Запишите полученные значения с учетом систематической погрешности.

14. Найдите отношение коэффициента жесткости пружины к ее длине и , оцените погрешность найденных величин. Запишите полученный результат.

15. Сравните и . Сделайте вывод.

II. Определение массы груза с помощью пружинного маятника.

1. Подвесьте на 1 пружине груз неизвестной массы.

2. Вызовите вертикальные колебания груза небольшой амплитуды (2 – 3 см).

3. Измерьте время, за которое груз совершает 40 колебаний.

4. Опыт повторите 6 раз. Данные занесите в таблицу 2.

5. Определите период колебаний груза, его среднее значение. Данные занесите в таблицу 2.

6. Вычислите погрешность периода с учетом случайной и систематической погрешностей.

7. Запишите полученный результат .

8. Определите массу неизвестного груза, используя формулу (5) и значение коэффициента жёсткости для этой пружины.

9. Определите погрешность измерения 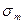. Запишите полученный результат

10.Подвесьте на 2 пружине тот же груз «неизвестной» массы.

11. Проделайте действия, аналогичные п.п. 1 – 9. По окончании измерений снимите груз с пружины.

12.Взвесьте груз неизвестной массы на электронных весах. Запишите результат, с учетом систематической погрешности .

Таблица 2.

	№	N	t_i, c	T_i, c	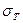, c	, c
1 пружина	1
	2
	3
	4
	5
	6
2 пружина	1
	2
	3
	4
	5
	6

13.Сравните результаты, измерения массы , и . Сделайте вывод.

Контрольные вопросы.

1.Что такое колебания?

2.Приведите пример колебательных процессов.

3.Какие колебания называются периодическими?

4.Что такое период колебаний, в каких единицах измеряется период колебаний?

5.Что такое частота колебаний, в каких единицах измеряется частота в системе СИ?

6.Что такое амплитуда, колебаний, в каких единицах измеряется амплитуда колебаний?

7.Какие колебания называются гармоническими?

8.Запишите формулу для периода гармонических колебаний, поясните величины, входящие в неё.

9.Что такое циклическая частота? Запишите формулу связи между циклической частотой и частотой?

10. Что такое фаза колебаний, начальная фаза колебаний?

11. Какое уравнение называют дифференциальным уравнением гармонических колебаний?

12. Как связаны между собой координата, скорость, ускорение при колебаниях?

13. Какие колебания называются свободными?

14. Какие колебания называются вынужденными?

15. Какую систему называют маятником?

16. Что такое пружинный маятник?

17. Чему равна циклическая частота колебаний пружинного маятника?

18. Чему равен период колебаний пружинного маятника?

19. С какой частотой происходят колебания кинетической энергии маятника?

20. С какой частотой происходят колебания потенциальной энергии маятника?

21. От чего зависит коэффициент жесткости пружины?.

Рекомендуемая литература.

1. Сивухин Д. В. Общий курс физики. Т. I. Механика.- М.: Наука, 1979.

2. Стрелков С. П. Механика.- М.: Наука, 1975, 560 с.

3. Методическое пособие по обработке результатов измерений, Мн., МГЭУ, 2005, 36 с.

Литература, использованная при подготовке пособия.

1. Физика: задание №4 для 11-х классов (2002-2003 учебный год).Сост.: В.И.Чивилев, - М.: МФТИ, 2002, 32 с.

2. Стрелков С. П. Механика.- М.: Наука, 1975, 560 с.

3. Элементарный учебник физики: Учебное пособие. т.3/ под ред. Г.С.Ландсберга,-М.: «Шрайк», 1995 – 608 с.

4. Лабораторный практикум по общей физике: Учебное пособие. т.1/ А.Д.Гладун, Д.А.Александров, Ф.Ф.Игошин и др., под ред. А.Д.Гладуна. -М.: МФТИ, 2004 – 316 с.

5. Физическая энциклопедия / Гл. ред. А. М. Прохоров. Ред. кол. Д. М. Алексеев, А. М. Балдин, А. М. Бонч-Бруевнч, А. С. Боровик-Романов и др.- М.: Сов. энциклопедия. Т. 1. Аронова – Бома эффект – Длинные линии. 1988. 704 с, ил.

Дата добавления: 2018-11-24; просмотров: 977; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 Следующая ⇒

Мы поможем в написании ваших работ!