Типы неопределенностей и их раскрытие
Все пределы можно условно разделить на несколько типов, каждый из которых имеет свой способ решения.
I тип. Пределы, содержащие дробно-рациональные или иррациональные функции и дающие неопределенность вида 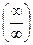 вычисляются путем деления числителя и знаменателя на х в старшей степени дроби.
вычисляются путем деления числителя и знаменателя на х в старшей степени дроби.
Пример 4.18.
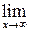
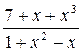 = (при подстановке вместо х бесконечно большой величины получим неопределенность вида
= (при подстановке вместо х бесконечно большой величины получим неопределенность вида 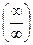 ; а так как х3старшая степень всей дроби, то поделим на нее и числитель, и знаменатель)
; а так как х3старшая степень всей дроби, то поделим на нее и числитель, и знаменатель)
= 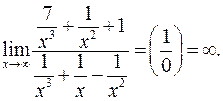
Пример 4.1 9 .
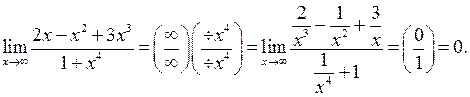
Пример 4. 20 .
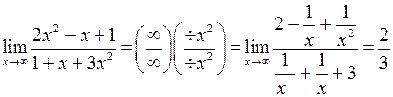 .
.
Пример 4.2 1 .
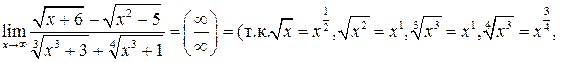
то старшая степень будет х1) =
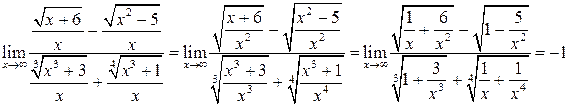 .
.
Можно вывести общее правило для этого типа пределов: если степень числителя равна степени знаменателя, то предел равен отношению коэффициентов, стоящих при этих степенях; если степень числителя больше степени знаменателя, то предел равен бесконечности; если степень числителя меньше степени знаменателя, то предел равен нулю.
II тип. Пределы, содержащие дробно-рациональные функции и дающие неопределенность 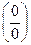 при х
при х  х0, решаются делением и числителя, и знаменателя на выражение (х – х0).
х0, решаются делением и числителя, и знаменателя на выражение (х – х0).
Пример 4.22.
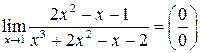
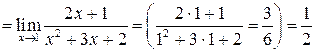 .
.


|

|


 2х2 –2х 2х + 1 x 3 – x 2 x2 + 3x + 2
2х2 –2х 2х + 1 x 3 – x 2 x2 + 3x + 2
|
|
х – 1 3x2 –3x
|
|
|

|
 0 2x – 2
0 2x – 2
 2x – 2
2x – 2
0
Пример 4.23.
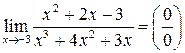 =
= 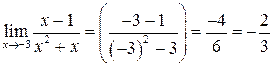 .
.


|
|

 x2 + 3x x – 1 x3 + 3x2 x2 + x
x2 + 3x x – 1 x3 + 3x2 x2 + x

|
|
– x – 3 x2 + 3x

 0 0
0 0
III тип. Пределы, содержащие иррациональные функции и дающие неопределенности 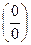 или (
или (  ), вычисляются домножением и числителя, и знаменателя на сопряженное выражение, приводящее к формулам разности квадратов, или разности (сумме) кубов.
), вычисляются домножением и числителя, и знаменателя на сопряженное выражение, приводящее к формулам разности квадратов, или разности (сумме) кубов.
Пример 4.2 4 .
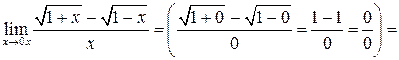
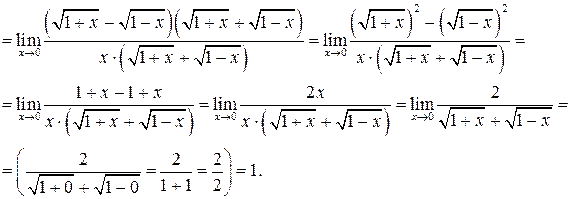
Пример 4.2 5 .
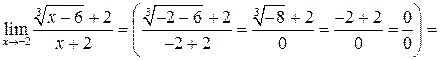
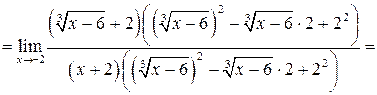

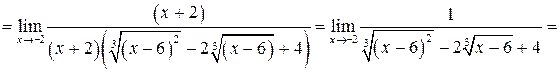
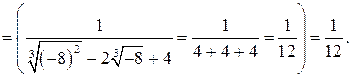
Пример 4.2 6 .
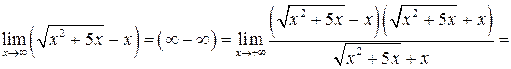
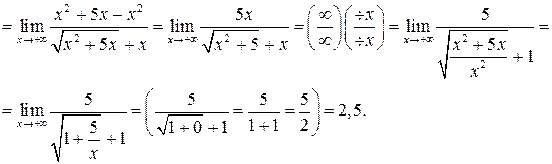
IV тип. Таблица эквивалентных функций при 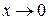 .
.
1) sinx ~ x,
2) tgx ~ x,
3) arcsinx ~ x,
4) arctgx ~ x,
5) ln(1+x) ~ x,
Следствие. loga(1+x) ~ xlna.
6) ax –1 ~ xlna,
Следствие. ex –1 ~ x,
|
|
|
7) (1+ x)m –1 ~ mx.
Пример 4.27.

Пример 4.28.
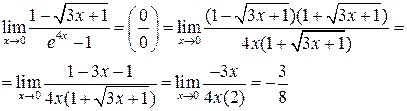
Пример 4.29.
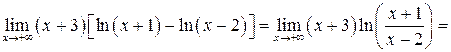
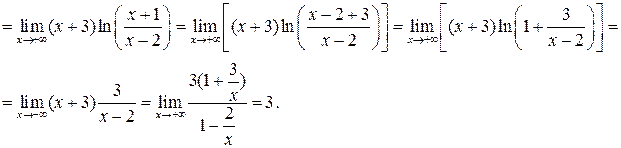
Пример 4.30.
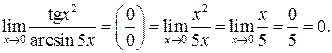
Пример 4.3 1 .
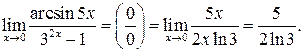
Непрерывность функций
Определение 4.4.1. Функция у = f(x) называется непрерывной в точке х0, если одновременно выполняются следующие условия:
1) существует значение функции в этой точке 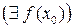 ;
;
2) существуют односторонние пределы функции в этой точке и они равны между собой 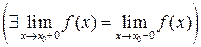 ;
;
3) значение функции в этой точке равно односторонним предельным значениям 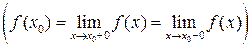 .
.
Исходя из определения предела функции, можно получить два варианта определения непрерывности в точке:
«по Коши»  ,
,
«по Гейне» 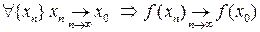 .
.
Введем обозначения:
приращение аргумента 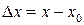 ,
,
приращение функции 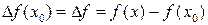 .
.
Тогда определение непрерывности в точке х0 может звучать так: при малых приращениях аргумента малым становится и приращение функции.
Теорема 4.4.1.
Пусть функции 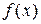 и
и 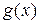 непрерывны в точке х0. Тогда функции
непрерывны в точке х0. Тогда функции  ,
, 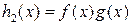 непрерывны в точке х0. Если
непрерывны в точке х0. Если 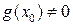 , то функция
, то функция 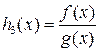 также непрерывна в точке х0.
также непрерывна в точке х0.
Доказательство.
Оно сразу же следует из теоремы 4.3.3 «предел и арифметика для функций».
Определение 4.4.2. Пусть f – некоторая функция, 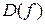 – её область определения. Назовём функцию f непрерывной на интервале
– её область определения. Назовём функцию f непрерывной на интервале 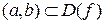 , если f непрерывна в любой точке этого интервала.
, если f непрерывна в любой точке этого интервала.
|
|
|
Назовём функцию f непрерывной на отрезке 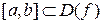 , если f непрерывна на интервале (a , b), непрерывна справа в точке a и непрерывна слева в точке b .
, если f непрерывна на интервале (a , b), непрерывна справа в точке a и непрерывна слева в точке b .
Примеры непрерывных функций:
1) 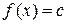 непрерывна на всей числовой прямой.
непрерывна на всей числовой прямой.
Доказательство.
Пусть 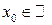 и произвольна, тогда
и произвольна, тогда 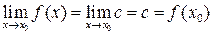 .
.
2) 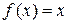 непрерывна на всей числовой прямой.
непрерывна на всей числовой прямой.
Доказательство.
Пусть 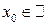 и произвольно, тогда из условия
и произвольно, тогда из условия 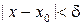 нужно получить
нужно получить 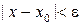 . Пусть e>0 и произвольно. Выберем
. Пусть e>0 и произвольно. Выберем 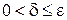 , d –искомое.
, d –искомое.
3) многочлен 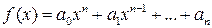 непрерывен на всей числовой прямой.
непрерывен на всей числовой прямой.
Доказательство следует из теоремы 4.4.1.
4) 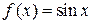 непрерывна на всей числовой прямой.
непрерывна на всей числовой прямой.
Доказательство.
Пусть 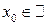 и произвольно.
и произвольно.
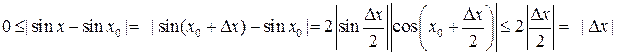 .
.
Если 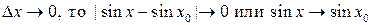 .
.
Аналогично можно доказать непрерывность 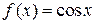 на
на  .
.
5) 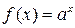 непрерывна на всей числовой прямой.
непрерывна на всей числовой прямой.
6) 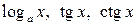 – непрерывны на области определения.
– непрерывны на области определения.
Определение 4.4.3. Если хотя бы одно из условий в определении непрерывности нарушается, то точка х0 называется точкой разрыва.
Классификация точек разрыва:
1. Если существует конечный предел f(x) при х → х0, но не равный f(x0), точка разрыва х0 называется точкой разрыва 0 рода или устранимый разрыв (рис.4.21). Так как в этом случае возможно переопределение функции в точке х0 так, чтобы она стала непрерывной.
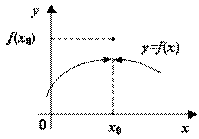
Рис. 4.21. х0 – точка устранимого разрыва
|
|
|
2. Говорят, что х0 – точка разрыва I рода, если функция не определена в точке х0, значения функции не равно предельному или односторонние пределы не равны между собой (рис.5.22).
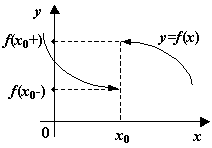
Рис. 4.22. х0 – точка разрыва I рода
3. Если нарушается первое условие в определении непрерывности и хотя бы один из односторонних пределов не существует (равен 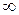 ), то говорят, что х0 – точка разрыва II рода (рис.5.23).
), то говорят, что х0 – точка разрыва II рода (рис.5.23).
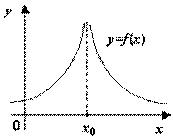
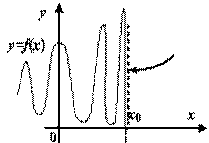
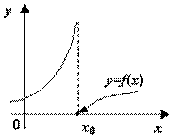
Рис. 4.23. х0 – точка разрыва II рода. Некоторые варианты
Пример 4.31.
Исследовать функцию 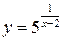 на непрерывность в точках х1 = 2 и х2=4. Сделать схематический чертеж.
на непрерывность в точках х1 = 2 и х2=4. Сделать схематический чертеж.
Решение.
Проверим выполнение всех трех условий непрерывности для каждой точки.
Для х1 = 2:
1) 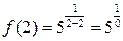 – значение функции не существует
– значение функции не существует 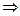 это точка разрыва.
это точка разрыва.
2)  ,
,
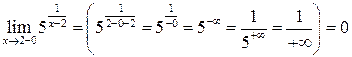 .
.
Так как один предел равен бесконечности, то это точка разрыва II рода.
Для х2 = 4:
1)  .
.
2) 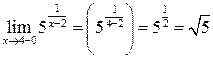 ,
,
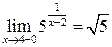
3) 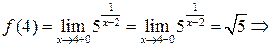 эта точка является точкой непрерывности.
эта точка является точкой непрерывности.
Сделаем схематический чертеж в окрестности данных точек (рис. 4.24).
|


|
|
|

|

Рис. 4.24. График функции примера 4.31
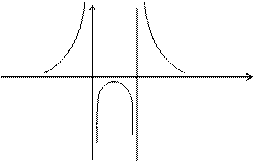
Пример 4.32.
Исследовать функцию 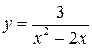 на непрерывность в точках х1 = 0 и х2= 2. Сделать чертеж.
на непрерывность в точках х1 = 0 и х2= 2. Сделать чертеж.
Решение.
Для х = 0:
1) 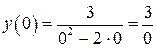 – не существует
– не существует 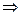 точка разрыва.
точка разрыва.
2) 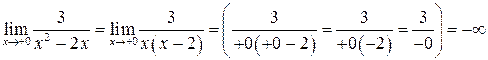 ,
,
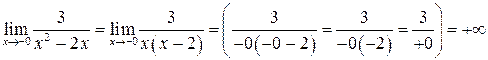 .
.
Так как оба предела равны 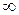 , то это точка разрыва II рода.
, то это точка разрыва II рода.
Для х = 2:
1) 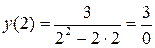 – не существует
– не существует 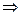 это тоже точка разрыва.
это тоже точка разрыва.
2) 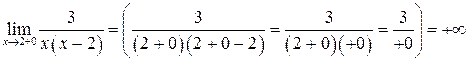 ,
,
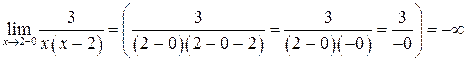
Следовательно, эта точка разрыва II рода (рис. 4.25).
 |
|
|
|
х
Рис. 4.25. Схематический чертёж функции примера 4.32.
Дата добавления: 2018-11-24; просмотров: 262; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

