Задача 1. Продажа холодильников
Лабораторная работа №1
Обработка и анализ статистической информации на основе группировки
Структура лабораторной работы
Постановка задачи
Алгоритм группировки
Пример
Задачи для самостоятельной работы
Вопросы по теме
Постановка задачи
Получена информация (выборка) – значения одного или нескольких показателей по анализируемой проблеме.
Рассмотрим одномерные массивы (наблюдения за одним показателем).
Примеры: объемы продаж некоторого товара за день, неделю, месяц; число посетителей кинозала; цены на объекты недвижимости, число обращений в службу спасения в день и т.д.
Требуется получить ответы на следующие вопросы:
· Какую полезную информацию предоставляет собранный материал?
· Как обработать эти данные и установить существующие закономерности для того, чтобы в дальнейшем достаточно достоверно прогнозировать, например, доходность или размер эксплуатационных затрат?
· Какие значения показателя являются наиболее типичными (ожидаемыми)?
· Как, например, используя имеющуюся статистику, оценить шансы того, что изучаемый показатель будет находиться в некотором конкретном диапазоне значений или не превысит некоторого критического уровня?
Алгоритм группировки
Группировка данных — разбиение всего диапазона изменения показателя на группы (интервалы) с подсчетом числа наблюдений (частот), попавших в ту либо иную группу, или их доли (относительных частот). Это позволяет оценить, в каких интервалах значений исследуемая величина появляется чаще, а в каких реже.
|
|
|
1) группировка приводит к потере части информации,
2) но позволяет преобразовать неупорядоченный набор выборочных данных таким образом, что становится понятным, насколько часто значения исследуемой величины появляются в том или ином диапазоне ее значений.
Алгоритм группировки
1. Проранжировать данные. Найти минимальное Ymin и максимальное Ymах значения среди выборочных данных.
2. Весь диапазон изменения величины Y — от Ymin до Ymах — разбить на интервалы (карманы) одинаковой длины. Количество интервалов (k) и их длину определить, исходя из содержательного смысла анализируемого показателя и задач исследования. На практике число интервалов обычно выбирают не менее 5 и не более 15.
3. Подсчитать, сколько наблюдений попало в каждый из таких интервалов, т.е. частоты:
4. Вычислить относительные частоты — доли наблюдений, оказавшихся в том или ином интервале, удобнее вычислять в процентах:
5. Результаты вычислений свести в таблицу (табл.).
6. В зависимости от цели анализа на основе данных 2-й или 3-й графы таблицы построить график — гистограмму, характеризующую особенности распределения исследуемого показателя в зависимости от его значений.
|
|
|
Таблица
Характеристика сгруппированных данных
| Интервал | Частота ni число наблюдений, попавших в интервал | Относительная частота Р i (доля наблюдений, оказавшихся в интервале) | Относительная частота Р i % (доля в процентах) |
Пример
Число посетителей кафе в период бизнес-ланча колеблется от 16 до 25 человек. Для своевременного обслуживания посетителей владелец кафе должен обеспечить в этот период соответствующее количество обслуживающего персонала и необходимый запас продуктов. Информация (статистика) о числе посетителей кафе за последние 50 дней приведена в табл. Excel
Задание
1. На какое число посетителей целесообразно ориентироваться, чтобы правильно определить запас необходимых блюд и назначить оптимальное количество сотрудников, обслуживающих клиентов?
2. Как оценить шансы того, что число посетителей не превысит, например, 28 человек
Построение рядов распределения и гистограмм в Excel
Решение.
1. Ввести исходные данные (значения переменной Число посетителей) на рабочий лист в столбец А., как показано на рис.1 и отсортировать по возрастанию с помощью пункта меню Сортировать. Определить минимальное и максимальное значения (это нужно для интерпретации результатов).
|
|
|
2. Разбить диапазон значений переменной Число посещений на интервалы одинаковой длины (взять для данного примера -9 интервалов: до 16, (16,18], (18,20], (20,22],, (30,32]). (……] – эта запись означает, что левое значение не входит в этот интервал, а правое входит. Значения правых границ интервалов 16, 18, 20, …, 22 ввести в столбец рядом с исходными данными, например, B2-B10 (как на рабочем листе в файле Excel).
Эти числа определяют правые границы интервалов, например, первый интервал будет таким (0, 16]. Первый интервал всегда определяется таким образом, чтобы правой границей этого интервала было наименьшее значение изучаемого показателя. (……]. Не забудьте ввести название столбца.
| Столбец № Строки | A | В |
| 1 | число посетителей за 50 дней | интервалы |
| 2 | 24 | 16 |
| 3 | 26 | 18 |
| 4 | 18 | 20 |
| 5 | 23 | 22 |
| 6 | 25 | 24 |
| 7 | 22 | 26 |
| 8 | 24 | 28 |
| 9 | 23 | 30 |
| 10 | 22 | 32 |
| … | … | |
| 48 | 17 | |
| 49 | 22 | |
| 50 | 25 |
| Рис. 1. Исходные данные |
Для группировки данных, построения ряда распределения и гистограмм используют инструмент ГИСТОГРАММА.
|
|
|
3. Для подсчета частот (количества данных выборки, попавших в тот или иной карман) и графического представления ряда распределения необходимо вызвать инструмент «Гистограмма» «Пакета анализа»: пункт меню Данные -> Анализ данных... Гистограмма.
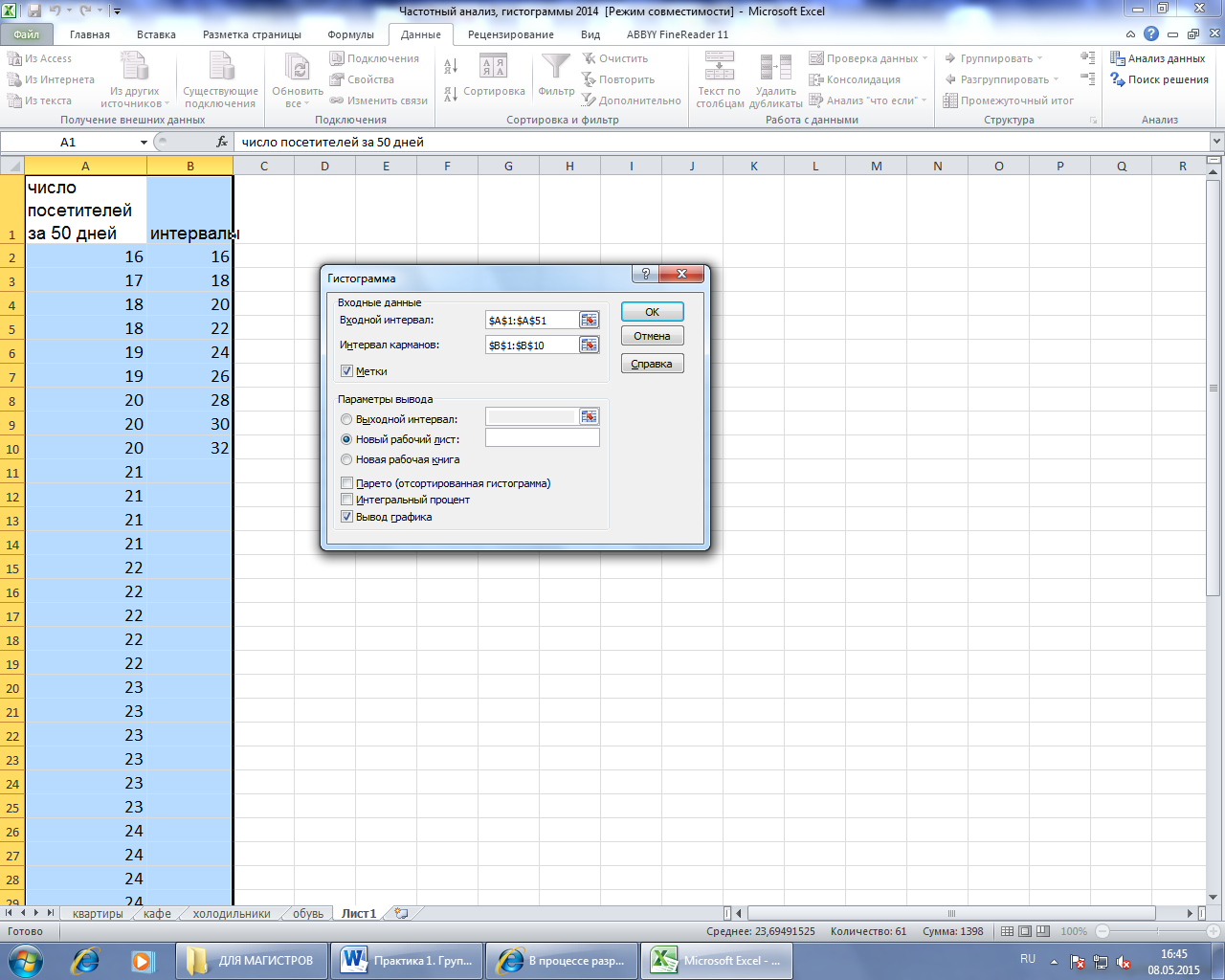
4. В диалоговом окне Гистограмма ввести в соответствующие поля входные данные вместе с заголовком и интервал карманов вместе с заголовком.
После ввода информации и нажатия клавиши ОК в ячейках L1 —М8 примера вывода результатов (рис.2) появится таблица, и на рабочий лист будет выведена гистограмма ряда распределения (рис.3). Для получения классической гистограммы, аналогичной той, которая изображена на рис.3, следует установить галочку у надписи «Вывод графика».
Если в окне «Интервал карманов» не указывать адреса ячеек с границами, то Excel самостоятельно разобьет диапазон Ymin — Ymax на карманы и подсчитает количество значений выборочных данных, находящихся в каждом из них. Однако делать это не рекомендуется, так как чаще всего такое автоматическое разбиение не всегда соответствует задачам реального анализа. Кроме того, границы интервалов при автоматическом разбиении могут оказаться не целыми числами, что не всегда соответствует реальным выборочным данным, отражающим, например, число покупателей, количество проданных единиц техники и т.д.
Для графического представления ряда распределения инструмент «Гистограмма» предлагает три вида графиков:
1) классическая гистограмма
2) частотное распределение в виде отсортированной гистограммы Парето.
3)интегральный процент выводит график накопленной частоты, выводится совместно с гистограммой, либо с отсортированной гистограммой Парето.
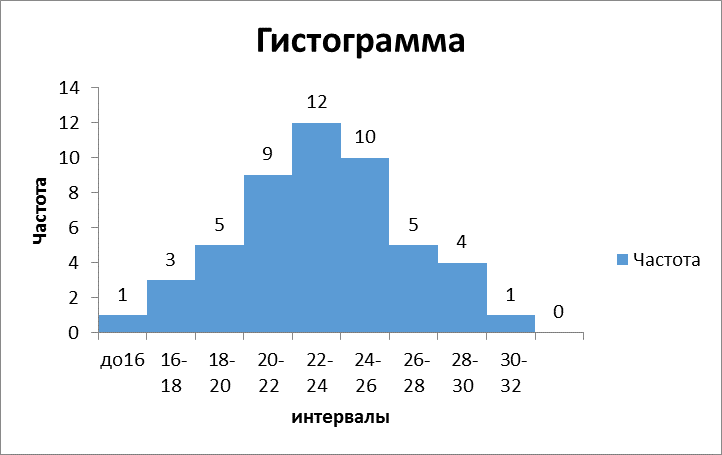
Рис.2. Гистограмма
5. Инструмент «Гистограмма» подсчитывает только частоты число наблюдений, попавших в тот или иной карман. Для вычисления относительных частот (доли наблюденийв процентах) результирующую таблицу необходимо расширить, т.е. дополнить столбцом и ввести в нем соответствующие расчетные формулы (ячейки № 2 — 8 на рис.1).
На основе этих данных можно дополнительно построить гистограмму относительных частот (рис. 3). Для этого используют пункт меню Вставка -> Гистограмма.
Во многих задачах бизнеса гистограммы относительных частот (долей) являются более полезными и информативными, нежели гистограммы частот, поскольку позволяют получить оценки вероятностей тех или иных событий.
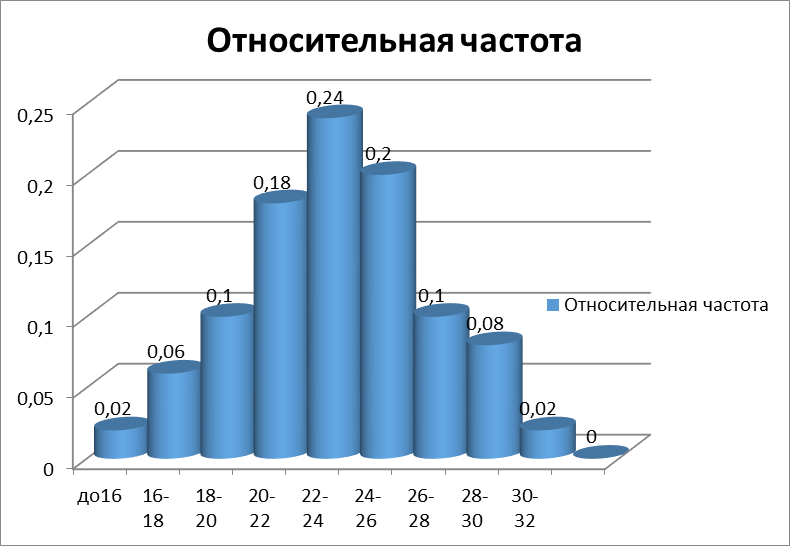
Рис.3. Гистограмма относительных частот
С содержательной точки зрения каждый интервал определяет конкретное событие. Например, интервал от 26 до 28 человек (26-28] соответствует событию «кафе посетят от 26 до 28 человек». Следовательно, относительная частота является оценкой вероятности такого события и составит Р (число посетителей будет от 26 до 28 человек включительно)=5/50=0,1 (10%).
Для графического представления ряда распределения инструмент «Гистограмма» предлагает три вида графиков:
1) классическая гистограмма
2) частотное распределение в виде отсортированной гистограммы Парето. Столбцы гистограммы будут расположены в порядке убывания по высоте слева направо – от интервала с максимальной частотой к интервалу с минимальным значением частоты.
3) интегральный процент выводит график накопленной частоты (интегральная кривая), выводится совместно с гистограммой, либо с отсортированной гистограммой Парето. Интегральная кривая для каждого значения Y показывает процент выборочных данных, принявших значение меньшее, чем Y .
4. Ответы на вопросы задания:
Минимальное число посетителей кафе -16 человек, а максимальное – 32 человека.
Таким образом, чаще всего (в 24% случаев) кафе посещают от 22 до 24 человек. По данным выборки в период бизнес-ланча в 62% случаев (18% + 24% + 20%) кафе посещают от 20 до 26 человек.
Вероятность того, что число посетителей не превысит 28 человек, можно оценить следующим образом: 100% - (8%+ 2%)=90%.
Конец примера
4. Задачи для самостоятельной работы
Задача 1. Продажа холодильников
Информация, собранная владельцем магазина бытовой техники о дневных продажах холодильников за 7 недель приведена в таблице.
Задание. На основе имеющихся данных:
1) установить наиболее вероятные объемы дневных продаж и диапазон их возможных изменений;
2) оценить шансы того, что в течение дня будет продаваться не менее 25 холодильников;
Дата добавления: 2018-11-24; просмотров: 1423; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
