Геометрический смысл теоремы Лагранжа
На основании формулы 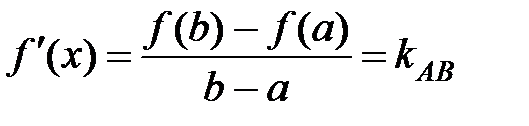 можно утверждать следующее.
можно утверждать следующее.

|
Если график функции y = f(x) непрерывный на отрезке 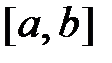 и гладкий на интервале и гладкий на интервале 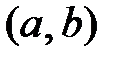 , то на этом интервале найдется такая точка , то на этом интервале найдется такая точка 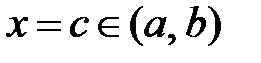 , в которой касательная параллельна хорде, стягивающей граничные точки графика функции (рис. 28). , в которой касательная параллельна хорде, стягивающей граничные точки графика функции (рис. 28).
|
2. Частное решение линейного неоднородного дифференциального уравнения n-ого порядкас постоянными коэффициентами.Вид частного решения неоднородного дифференциального уравнения
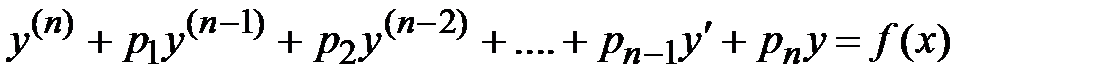 зависит от вида правой части этого уравнения (функции
зависит от вида правой части этого уравнения (функции 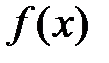 ) и от величин корней характеристического уравнения. Рассмотрим нахождение частного решения для двух видов функции
) и от величин корней характеристического уравнения. Рассмотрим нахождение частного решения для двух видов функции 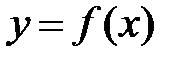 . Случай 1. Правая часть уравнения
. Случай 1. Правая часть уравнения 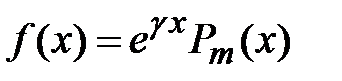 , где g- вещественное значение,
, где g- вещественное значение, 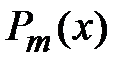 - многочлен m-й степени. В этом случае частное решение уравнения ищется в виде
- многочлен m-й степени. В этом случае частное решение уравнения ищется в виде 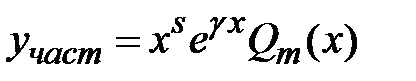 ,где
,где 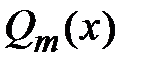 - многочлен m-й степени, s- степень кратности корня характеристического уравнения
- многочлен m-й степени, s- степень кратности корня характеристического уравнения 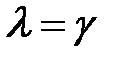 . Если
. Если 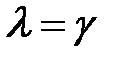 не является корнем характеристического уравнения, то s = 0. Случай 2. Правая часть неоднородного дифференциального уравнения имеет вид
не является корнем характеристического уравнения, то s = 0. Случай 2. Правая часть неоднородного дифференциального уравнения имеет вид 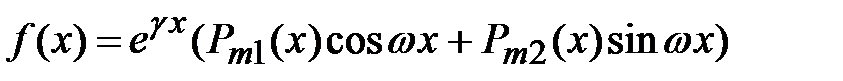 , где g и w- вещественные значения,
, где g и w- вещественные значения,  и
и  - многочлены степени
- многочлены степени  и
и  соответственно. В этом случае частное решение дифференциального уравнения ищется в виде
соответственно. В этом случае частное решение дифференциального уравнения ищется в виде 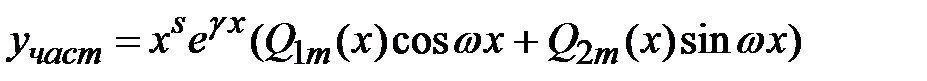 ,
, 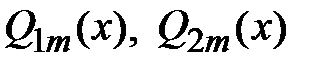 - многочлены степени
- многочлены степени 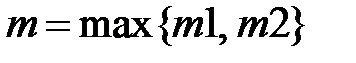 , s- кратность корня характеристического уравнения
, s- кратность корня характеристического уравнения  , где
, где  совпадает с числом g в показателе степени
совпадает с числом g в показателе степени 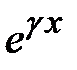 в функции
в функции  правой части уравнения. Если gв
правой части уравнения. Если gв  не совпадает с
не совпадает с  , то s = 0.
, то s = 0.
|
|
|
3. . Знакочередующиеся ряды. Теорема Лейбниц.Если члены знакочередующегося ряда  монотонно убывают
монотонно убывают  и стремятся к нулю
и стремятся к нулю  , то ряд сходится; причем сумма ряда по абсолютной величине не превосходит первого члена ряда
, то ряд сходится; причем сумма ряда по абсолютной величине не превосходит первого члена ряда  .
.
Д о к а з а т е л ь с т в о. По определению знакочередующегося ряда  предполагается, что члены ряда положительные
предполагается, что члены ряда положительные 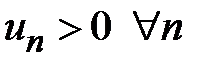 . Рассмотрим две частичные суммы ряда: с четным числом членов ряда
. Рассмотрим две частичные суммы ряда: с четным числом членов ряда  и с нечетным числом членов
и с нечетным числом членов  . В сумме с четным числом членов
. В сумме с четным числом членов  сначала сгруппируем члены попарно следующим образом
сначала сгруппируем члены попарно следующим образом  . Так как члены ряда монотонно убывают (
. Так как члены ряда монотонно убывают (  ), то разность в каждой скобке суммы
), то разность в каждой скобке суммы  больше нуля и эта сумма монотонно возрастает с увеличением числа членов 2n. Теперь сгруппируем члены этой суммы следующим образом
больше нуля и эта сумма монотонно возрастает с увеличением числа членов 2n. Теперь сгруппируем члены этой суммы следующим образом
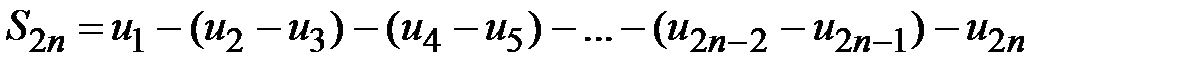 . Так как в этой сумме также разность в каждой скобке больше нуля, то сумма монотонно убывает с увеличением числа членов 2n и не превосходит первого члена ряда
. Так как в этой сумме также разность в каждой скобке больше нуля, то сумма монотонно убывает с увеличением числа членов 2n и не превосходит первого члена ряда  . Следовательно, последовательность частичных сумм ряда с четным числом членов монотонно возрастает и ограничена. Поэтому по теореме Вейерштрасса она имеет некоторый предел
. Следовательно, последовательность частичных сумм ряда с четным числом членов монотонно возрастает и ограничена. Поэтому по теореме Вейерштрасса она имеет некоторый предел  . Найдем также предел частичных сумм ряда с нечетным числом членов.
. Найдем также предел частичных сумм ряда с нечетным числом членов.  . При нечетном числе членов ряда сумма
. При нечетном числе членов ряда сумма  также не превосходит первого члена ряда
также не превосходит первого члена ряда  .
. 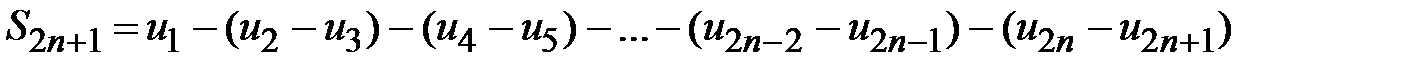 . Таким образом, предел частичных сумм знакочередующегося ряда существует, т. е. ряд всегда сходится, если его члены монотонно убывают и стремятся к нулю. Частичные суммы знакочередующегося ряда меньше первого члена ряда
. Таким образом, предел частичных сумм знакочередующегося ряда существует, т. е. ряд всегда сходится, если его члены монотонно убывают и стремятся к нулю. Частичные суммы знакочередующегося ряда меньше первого члена ряда  . Члены ряда стремятся к нулю
. Члены ряда стремятся к нулю  , поэтому сумма ряда не может превосходить первого члена ряда
, поэтому сумма ряда не может превосходить первого члена ряда  .
.
|
|
|
Билет 18.
Вывод формулы Тейлора
Теорема.Если в некоторой окрестности точки х = а функция 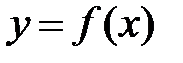 имеет конечные производные до (n+1)-го порядка включительно, то для любой точки этой окрестности справедлива формула
имеет конечные производные до (n+1)-го порядка включительно, то для любой точки этой окрестности справедлива формула
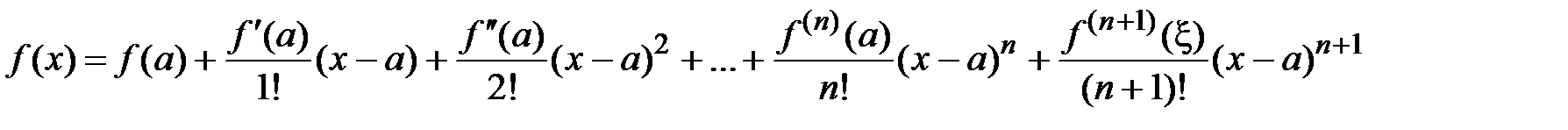 ,
,
где 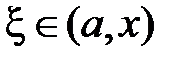 .
.
Доказательство. Используем теорему Ролля.
Обозначим 
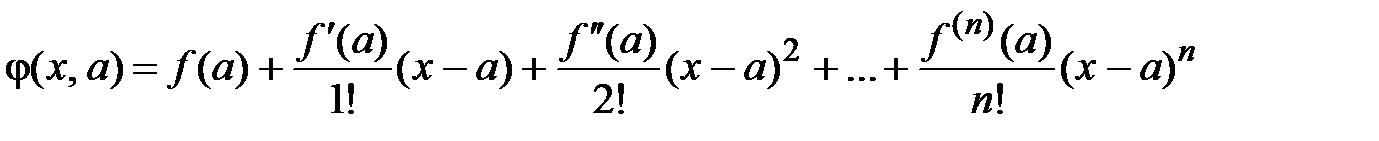 .Покажем, что разность
.Покажем, что разность 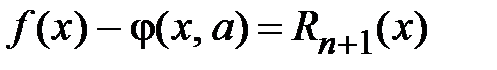 , где
, где 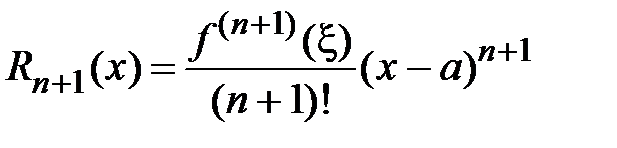 .
.
Для этого составим вспомогательную функцию 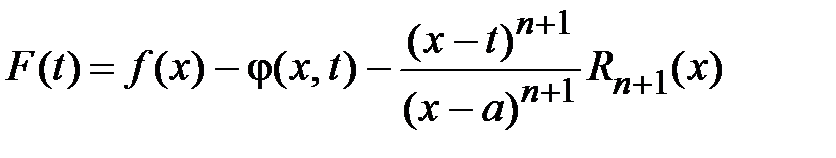
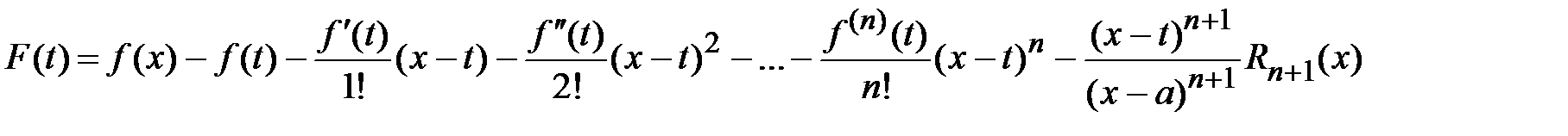
Найдем значения функции  в граничных точках отрезка
в граничных точках отрезка  .
.
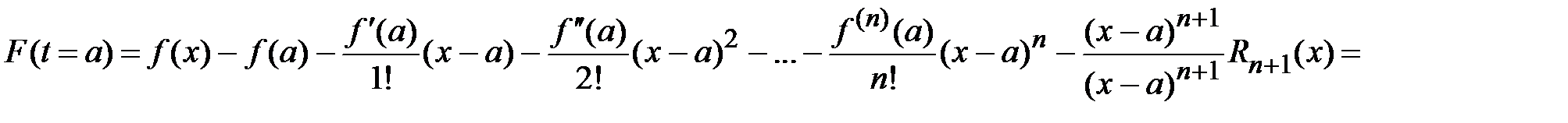
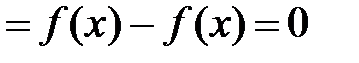 .
. 
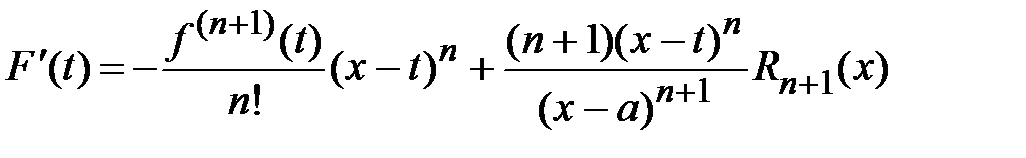 .
.
Найдем значение производной в точке t= x 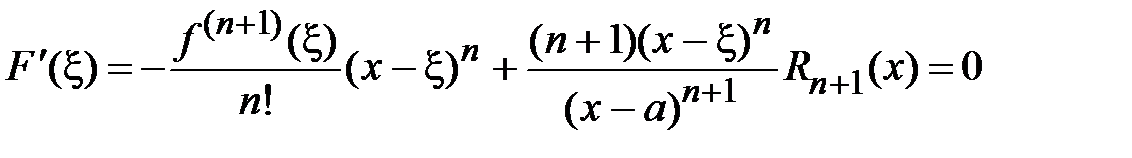 .
.
 .
.
выражение для  называется остаточным членом в форме Лагранжа.Если представить x в виде
называется остаточным членом в форме Лагранжа.Если представить x в виде  , где
, где  , то остаточный член примет вид
, то остаточный член примет вид
 .
.
В частном случае, если 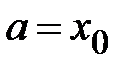 ,
,  , то формула Тейлора примет вид
, то формула Тейлора примет вид

Дата добавления: 2018-08-06; просмотров: 308; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
