Полный дифференциал функции нескольких переменных
Сумма первых двух слагаемых в выражении полного приращения Dz называется полным дифференциалом и записывается
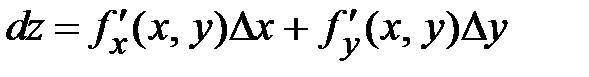 .В частном случае, если функция z = x, то
.В частном случае, если функция z = x, то  , т. е.
, т. е.  . Аналогично при z = y,
. Аналогично при z = y, 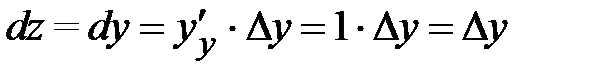 , т. е.
, т. е. 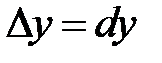 .Учитывая это, полный дифференциал запишем в виде
.Учитывая это, полный дифференциал запишем в виде 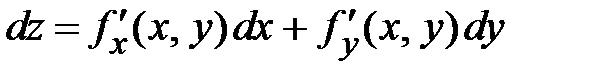 или
или 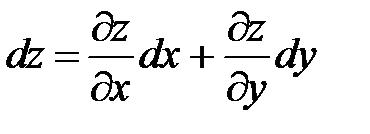 .
.
Следовательно, полное приращение функции  равняется сумме полного дифференциала и бесконечно малой величины более высокого порядка малости по сравнению с
равняется сумме полного дифференциала и бесконечно малой величины более высокого порядка малости по сравнению с  :
:  .
.
Найдем  ,т. е. полный дифференциал функции отличается от полного приращения на бесконечно малую функцию более высокого порядка малости по сравнению с Dx, Dy. Поэтому полный дифференциал называют главной линейной частью полного приращения функции.
,т. е. полный дифференциал функции отличается от полного приращения на бесконечно малую функцию более высокого порядка малости по сравнению с Dx, Dy. Поэтому полный дифференциал называют главной линейной частью полного приращения функции.
Определение полного дифференциала функции нескольких переменных. Полным дифференциалом функции нескольких переменных называется бесконечно малая функция прямо пропорциональная бесконечно малым приращениям независимых переменных и отличающаяся от полного приращения функции на бесконечно малую функцию более высокого порядка малости по сравнению бесконечно малыми приращениями независимых переменных.
2.Теорема о существовании первообразной функции. Для любой непрерывной функции существует бесконечное множество первообразных функций, отличающихся друг от друга на постоянную величину. Д о к а з а т е л ь с т в о. 1. Покажем, что для функции  существует первообразная функция
существует первообразная функция 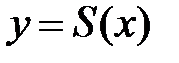 , являющаяся площадью криволинейной трапеции с переменной граничной прямой (рис. 56).
, являющаяся площадью криволинейной трапеции с переменной граничной прямой (рис. 56).
|
|
|
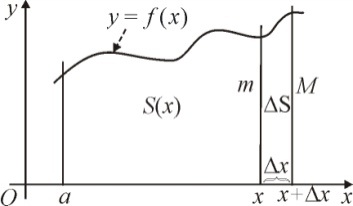 Пусть правая граничная прямая изменяет положение от х до
Пусть правая граничная прямая изменяет положение от х до 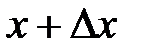 . На этом отрезке
. На этом отрезке 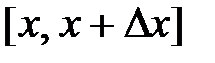 непрерывная функция
непрерывная функция  достигает своего наибольшего М и наименьшего m значений
достигает своего наибольшего М и наименьшего m значений 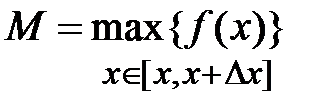 ,
, 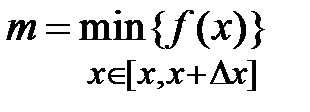 .Очевидно, значение площади элементарной криволинейной трапеции
.Очевидно, значение площади элементарной криволинейной трапеции  на отрезке
на отрезке 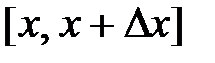 удовлетворяет неравенству
удовлетворяет неравенству 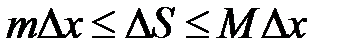 . Поделим это неравенство на
. Поделим это неравенство на 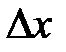 , получим
, получим 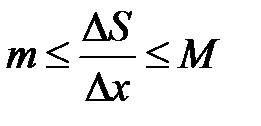 . При
. При 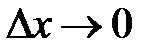 наибольшее и наименьшее значения функции на этом отрезке стремятся к одной и той же величине
наибольшее и наименьшее значения функции на этом отрезке стремятся к одной и той же величине 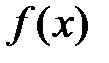 ,
, 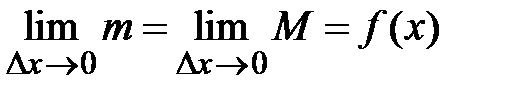 .
.
По теореме о промежуточной функции 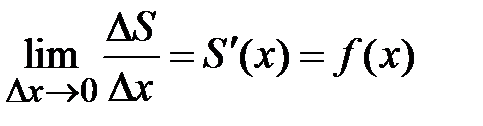 , т. е.
, т. е. 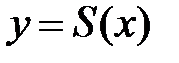 является первообразной для функции
является первообразной для функции  .
.
2. Покажем, что для данной функции существует бесконечное множество первообразных функций. Действительно, если к данной функции прибавить любую постоянную величину, то ее производная не изменится 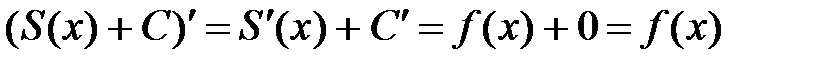 ,
,  .
.
3. Покажем также, что любые две первообразные функции отличаются друг от друга на постоянную величину. Пусть  и
и  первообразные функции для
первообразные функции для  . Тогда
. Тогда 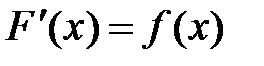 и
и  . Найдем их разность, получим
. Найдем их разность, получим 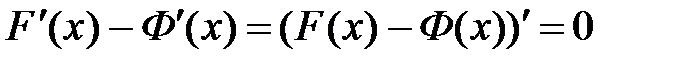 . Если производная функции равна нулю, то функция является постоянной. Следовательно,
. Если производная функции равна нулю, то функция является постоянной. Следовательно, 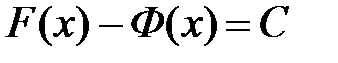 , где
, где 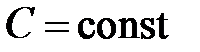 , и
, и 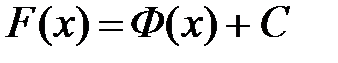 .
.
Признак Даламбера сходимости знакоположительных рядов
Если для знакоположительного ряда 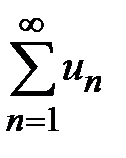 существует предел отношения последующего члена ряда к предыдущему при неограниченном возрастании их номеров, т. е. существует предел
существует предел отношения последующего члена ряда к предыдущему при неограниченном возрастании их номеров, т. е. существует предел  , то:еслиr< 1, то ряд сходится; 2) если r> 1, то ряд расходится;3) если r = 1, то данный признак не позволяет решить вопрос о сходимости ряда (ряд может как сходиться, так и расходиться).Д о к а з а т е л ь с т в о.1. Пусть
, то:еслиr< 1, то ряд сходится; 2) если r> 1, то ряд расходится;3) если r = 1, то данный признак не позволяет решить вопрос о сходимости ряда (ряд может как сходиться, так и расходиться).Д о к а з а т е л ь с т в о.1. Пусть 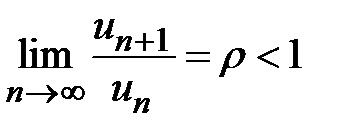 . Если r< 1, то всегда найдется число q, удовлетворяющее неравенству r<q< 1. В этом случае по определению предела существует такое число N, что если номер члена ряда n>N, то отношение
. Если r< 1, то всегда найдется число q, удовлетворяющее неравенству r<q< 1. В этом случае по определению предела существует такое число N, что если номер члена ряда n>N, то отношение 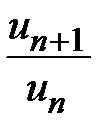 меньше этого числа q, т.е.
меньше этого числа q, т.е. 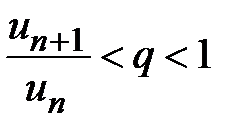 . Данное неравенство представим в следующем виде
. Данное неравенство представим в следующем виде  . Отношение
. Отношение  является отношением последующего члена ряда к предыдущему для бесконечной убывающей геометрической прогрессии
является отношением последующего члена ряда к предыдущему для бесконечной убывающей геометрической прогрессии  , которая сходится, так как знаменатель прогрессии меньше единицы (q< 1). В соответствии с теоремой 8.4 (третий признак сравнения рядов) ряд
, которая сходится, так как знаменатель прогрессии меньше единицы (q< 1). В соответствии с теоремой 8.4 (третий признак сравнения рядов) ряд 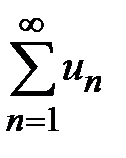 сходится.
сходится.
|
|
|
2. Пусть  . Тогда существует такое число q, которое больше единицы, но меньше r, т. е.
. Тогда существует такое число q, которое больше единицы, но меньше r, т. е. 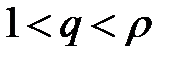 . В этом случае существует такое число N, что если номер члена ряда n>N, то отношение
. В этом случае существует такое число N, что если номер члена ряда n>N, то отношение 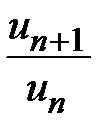 больше q, т. е.
больше q, т. е.  . Тогда по теореме 8.4 ряд
. Тогда по теореме 8.4 ряд 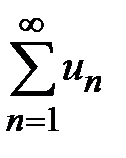 расходится.
расходится.
Данный признак Даламбера является наиболее простым и часто применяемым. Однако он дает ответ на вопрос о сходимости ряда только в тех случаях, когда ряд достаточно быстро сходится или расходится.
|
|
|
Билет 14.
Дата добавления: 2018-08-06; просмотров: 1221; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
