Случайная погрешность и ее модели
Случайные эффекты порождают разброс измеренных значений или показаний средства измерений.
Анализ случайной погрешности происходит после выполнения измерений, то есть после того, как все показания считаны или все измеренные значения получены. Поэтому, ISO, например, рекомендует степень близости измеренных значений (показаний) друг к другу называть особым словом «прецизионность», которое в зависимости от условий измерений конкретизируется еще двумя терминами «повторяемость (сходимость)» и «воспроизводимость» [1, 3, 11, 27]. Следовательно, случайная погрешность при выполнении измерений оценивается отдельно в условиях сходимости показаний и в условиях воспроизводимости измеренных значений.
Образно говоря, «грех» измерений здесь заключается лишь в том, что количество считываемых показаний (измеренных значений) не может быть доведено до бесконечности. За измеренное значение приходится принимать не математическое ожидание показаний, а лишь одно из случайных средних значений. Каждый раз при очередном повторном наборе показаний субъект получает другое среднее измеренное значение величины. В итоге мог бы появиться ряд (разброс) случайных средних измеренных значений величины, характеризующий случайную погрешность измерений. Однако для представления результата измерений находят только единственное среднее значение, что и вызывает неопределенность измерений.
|
|
|
При устремлении количества показаний к бесконечности случайная погрешность стремится к нулю.
Рекомендованное в литературе [22] определение термина «случайная погрешность измерений – составляющая погрешности измерений, изменяющаяся случайным образом» не позволяют использовать её в качестве показателя точности при представлении результата измерений. Чтобы она могла быть использована в этом качестве, ей необходимо сформулировать новое определение на основе её вероятностной природы.
| Случайная погрешность – показатель качества измерений, выраженный интервалом, в котором могла бы оказаться разность между средним измеренным значением величины и математическим ожиданием показаний (или измеренных значений) с заданной вероятностью. |
Поскольку математическое ожидание (как бы истинное значение) показаний всегда неизвестно, то рассматриваемая разность может иметь только вероятностный смысл. Поэтому в результате измерений эта погрешность может быть отражена только интервалом с указанием доверительной вероятности.
Поскольку в большинстве случаев измерения выполняются в условиях повторяемости [3, 11], то определение случайной погрешности при необходимости можно конкретизировать: случайная погрешность в условиях повторяемости – показатель качества измерений, выраженный интервалом, в котором могла бы оказаться разность между средним измеренным значением величины, полученным одним средством измерений (или одним методом или одной лабораторией) в одних и тех же условиях, и математическим ожиданием показаний (или измеренных значений) с заданной вероятностью.
|
|
|
В случае, когда измерения одной и той же величины выполняются несколькими разными методами и средствами измерений или в разных лабораториях, а за результирующее измеренное значение принимается среднее арифметическое полученных измеренных значений, то случайная погрешность отражает измерительный процесс уже в условиях воспроизводимости.
Случайная погрешность в условиях воспроизводимости – показатель качества измерений, выраженный интервалом, в котором могла бы оказаться разность между средним измеренным значением величины, полученным разными средствами измерений (разными методами или разными лабораториями), и математическим ожиданием измеренных значений с заданной вероятностью.
При необходимости дальнейшего суммирования составляющих погрешности измерений случайная погрешность может быть выражена выборочным стандартным отклонением S для среднего измеренного значения.
|
|
|
Если случайная погрешность измерений, например, существенно преобладает над систематической погрешностью и определена надежная (количество показаний более 30) оценка среднего квадратического отклонения σ, то для нормального закона распределения эта погрешность измерений может быть представлена интервалами как ±σ при вероятности Р = 0,68, или как ±2·σ при
Р = 0,95, или как ±3·σ при Р = 0,997.
Случайная погрешность (как характеристика прецизионности измерений) не имеет составляющих, она обусловлена только одной причиной – ограниченностью количества измеренных значений за конкретный период времени измерений (при одновременном воздействии всех случайных эффектов).
Если бы была возможность получить реальную непрерывную функцию распределения при бесконечном количестве показаний, то она содержала бы полную информацию о случайных измеренных значениях величины.
Поскольку это невозможно, то модель случайной погрешности всегда представляет собой дискретную (ступенчатую) функцию распределения в виде гистограммы.
|
|
|
Пример модели случайной погрешности в виде гистограммы плотности вероятности измеренных значений, построенной на основе экспериментальных данных, показан на рисунке 10.
| ρ[В] |
Вмин Вср Вмакс В
Рис. 10 – Гистограмма распределения плотности вероятностей
Рассеяние измеренных значений величины В характеризуют СКО, оценку которого вычисляют по формуле:
. (13)
Если выполнить новую серию измерений той же самой неизменной величины, то получим новое среднее измеренное значение и новую оценку СКО. Значит полностью избавиться от случайной составляющей погрешности невозможно.
Оценку СКО средних измеренных значений параметра относительно оценки математического ожидания вычисляют по формуле:
. (14)
Таким образом, формула (13) показывает уровень сходимости измеренных значений, который используется при представлении результата однократного измерения при условии, когда СКО подобных многократных измерений было оценено до выполнения этого (одного) измерения. Формула (14) позволяет оценить долю случайной погрешности при оценке общей погрешности выполненных измерений.
Видно, что СКО вычисленных средних измеренных значений параметра
в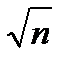 
меньше СКО самих измеренных значений величины.
Однако построение модели распределения в виде гистограмм требует большого количества измеренных значений, что не всегда возможно.
Для того, чтобы выразить случайную погрешность измерений доверительным интервалом при количестве измеренных значений менее 30, используют распределение Стьюдента. Оно описывает плотность распределения вероятности среднего арифметического, вычисленного по выборке из n случайных отсчетов нормально распределенной генеральной совокупности. Его вид зависит от числа отсчетов n, по которым находится среднее арифметическое значение, поэтому иногда говорят о семействе законов распределения Стьюдента. При увеличении n это распределение переходит в распределение Гаусса. При n £ 3 их СКО очень велико, то есть дисперсионная оценка разброса измеренных значений почти перестает существовать. Измеренных значений всегда должно быть более 3.
Случайную абсолютную погрешность полученного среднего измеренного значения находят по формуле:
, (15)
где 
– коэффициент Стьюдента при доверительной вероятности Р и количестве измеренных значений n, выбранная из таблицы 1;
– оценка СКО погрешности среднего значения, вычисленного по формуле (14).
Таблица 1 – Значения коэффициента tр для случайной величины,
имеющей распределение Стьюдента с n-1 степенями свободы
| n-1 | P = 0,95 | P = 0,99 | n-1 | P= 0,95 | P = 0,99 |
| 3 | 3,182 | 5,841 | 16 | 2,120 | 2,921 |
| 4 | 2,776 | 4,604 | 18 | 2,101 | 2,878 |
| 5 | 2,571 | 4,032 | 20 | 2,086 | 2,845 |
| 6 | 2,447 | 3,707 | 22 | 2,074 | 2,819 |
| 7 | 2,365 | 3,499 | 24 | 2,064 | 2,797 |
| 8 | 2,306 | 3,355 | 26 | 2,056 | 2,779 |
| 9 | 2,262 | 3,250 | 28 | 2,048 | 2,763 |
| 10 | 2,228 | 3,169 | 30 | 2,043 | 2,750 |
| 12 | 2,179 | 3,055 | ¥ | 1,960 | 2,576 |
| 14 | 2,145 | 2,977 |
На практике часто имеют не более 10 измеренных значений какого-либо параметра. Например, если считать 10 чисел от 0,1 до 1,0 с шагом 0,1 измеренными значениями величины В в единицах [В] с несущественной систематической погрешностью, то среднее арифметическое измеренное значение равно 0,55·[В]; СКО для среднего значения равно 0,09574 [В]. При n = 10 и вероятности 0,95 коэффициент Стьюдента равен 2,26. Тогда случайная составляющая абсолютной погрешности измерений равна ±0,216 [В].
и результат измерений может быть представлен в виде:
.
Если доверительную вероятность увеличить до 0,99, то коэффициент Стьюдента равен 3,25, доверительный интервал равен ±0,311 [В] и результат измерений уже будет другой:
.
Если количество измерений увеличить в три раза (например, 30), то интервал для истинного значения уменьшится всего на 10%.
Из этого примера видно, что погрешности выражают разными числовыми значениями при разной доверительной вероятности. Причем в первом случае интервал для истинного значения равен от 5,28 до 5,72, а во втором – от 5,19
до 5,81. Чем выше заданная вероятность, тем шире вычисленный интервал. Поэтому на практике ограничиваются заданной вероятностью 0,95 или 0,9. Ведь обработка измеренных значений параметра выполнена вероятностными методами с оценкой сверху, следовательно, границы для истинного значения измеряемой величины не могут быть абсолютно точными.
Случайная погрешность всегда оценивается на основе статистических методов обработки показаний. Она представляется двумя числами: числом вместе со знаком «±» и с указанием обозначения единицы величины [В]; значением вероятности Р нахождения математического ожидания показаний в пределах выбранного интервала. Если измерения одной и той же величины выполняются во времени несколькими рядами неравноточных измерений (с разными дисперсиями), то определяют средневзвешенное измеренное значение и средневзвешенное СКО [2, 11, 29].
Модели случайной погрешности измерений в виде гистограммы целесообразно указывать лишь при проведении высокоточных и ответственных измерений, а также в случаях, когда по условиям задачи необходимо сравнивать (сопоставлять) мало отличающиеся друг от друга измеряемые величины, например, при сличении эталонов.
В измерительной практике часто используют один объединенный показатель точности – интервал, отражающий одновременно влияние систематических и случайных эффектов, с указанием вероятности попадания истинного значения в этот объединенный интервал.
Дата добавления: 2018-06-01; просмотров: 640; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!