Теорема о промежуточных значениях непрерывной на отрезке функции.
Она же теорема Больцана-Коши
Пусть F(x) непрерывна на отрезке [a, b], F(a)=A, F(b)=B, A≠B и C – некоторое число, находящееся между A и B, тогда существует такое число cÎ [a ,b], что F(c)=C (причём число C достигается только если cÎ [a ,b] ).
Доказательство
Пусть A<B и A<C<B. Разделим [a, b] срединной точкой на 2 части и выберем ту часть [a1, b1], что F(a1)<C<F(b1) (т.е. тот, в котором оказалась точка С). Затем разделим и этот отрезок и т.д. Получим систему стягивающихся последовательностей [a, b]ɔ [a1,b1]ɔ… ɔ[an, bn] , притом длина стремится к нулю. Для такой системы существует единственная точка ε такая, что ε принадлежит [an, bn] , n є N, причём Lim(x->∞)an = Lim(x->∞)bn =ξ. Значит F(ξ) = C. По теореме о сжатой переменной C->F(ξ), следовательноF(ξ)=С.
Дифференцируемость функции в точке. Условия дифференцируемости функции в точке.
Определение.Функция y=f(x) называется дифференцируемой в точке x0, если ее приращение Δy в точке x0 может быть представлено в виде: Δy=A•Δx+α(Δx)•Δx, где A•Δx – линейная часть приращения, а α(Δx) - бесконечно малая функция от переменной Δx, т.е. limα(Δx)=0 при Δx→0.
Теорема. Для того, чтобы функция y=f(x) была дифференцируема в точке x0, необходимо и достаточно, чтобы она в этой точке имела конечную производную, причем A=f ‘ (x0).
Доказательство
Необходимость. Предположим: функция дифференцируема в точке x0, т.е. Δy=A•Δx+α(Δx)•Δx. Разделив обе части данного равенства на Δx, получим: Δy/Δx=A+α(Δx).
|
|
|
Достаточность. Пусть существует конечная производная y`(x0)∈R . Покажем дифференцируемость функции y`(x0)=lim (Δy/Δx) при Δx→0.
Если функция f(x) имеет конечный предел b при Δx→0 , то ее можно представить: f(x)=b+α(x) (α(x)→0) . Исходя из этого: Δy/Δx =y/(x0)+α(Δx), где limα(Δx)=0 при Δx→0, y/(x0) = Δy/Δx–α(Δx)→ A=y/(x0) . Теорема доказана.
Дифференцируемость и непрерывность.
Теорема о связи дифференцируемости и непрерывности.
Если функция y=y(x) дифференцируема в точке x0, то она и непрерывна в этой точке.
Справедливость утверждения следует из Δy=y/(x0)·Δx+α(Δx)·Δx и limΔx→0Δy=0, а по определению функция непрерывна, если малому приращению аргумента соответствует малое приращение функции.
Обратное утверждение не верно.
Например, функция y=∣x∣ непрерывна в точкеx=0, но не дифференцируема в этой точке.
Таким образом, не всякая непрерывная функция дифференцируема, а любая дифференцируемая функция непрерывна.
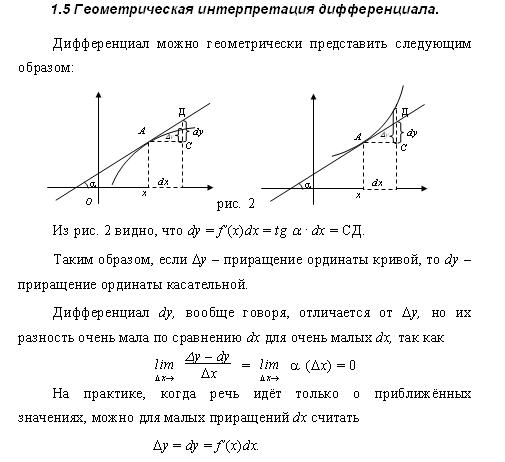
Дифференциал. Геометрическая интерпретация дифференциала.
Определение. Дифференциалом функции y=f(x) в точке x0 называется главная линейная относительно Δx часть приращения функции Δy в данной точке. y`=dy/dx.
|
|
|
Дата добавления: 2018-05-12; просмотров: 310; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
