Теорема Больцано — Вейерштрасса.
из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность.
пусть {Xn} ограниченная последовательность все её члены можно поместить в [a]b
 [a ][b1 ][b2 ]b x
[a ][b1 ][b2 ]b x
Разделим на равные части
Выделим один, содержащий бесконечное число членов последовательности
Выберем на этом отрезке 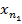 ещё разделим [b1 ]b пополам и выберем тот, где бесконечное число последовательности выберем
ещё разделим [b1 ]b пополам и выберем тот, где бесконечное число последовательности выберем 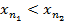 и так до [bn ]b,
и так до [bn ]b, 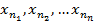 получим систему отрезков {
получим систему отрезков { 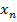 }.
}. 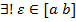 ( принадлежит всем отрезкам этой системы)
( принадлежит всем отрезкам этой системы)
Оказывается что 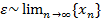
 (
(  [
[ 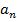 |
|  ]
] 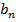 )
) 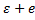
 Если
Если 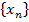 – неограниченно , то сходится либо к
– неограниченно , то сходится либо к 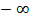 , либо к
, либо к 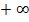
Наибольший предел 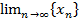 - верхний предел.
- верхний предел.
 Наименьший предел сходящейся последовательности
Наименьший предел сходящейся последовательности 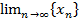 - нижний предел
- нижний предел
Пример 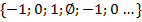 (1)
(1)
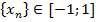
 {-1…-1} сходится к -1
{-1…-1} сходится к -1 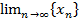 = - 1
= - 1
{0…0} сходится к 0 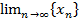 =0
=0
 {1…1} сходится к 1
{1…1} сходится к 1 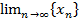 =1
=1
Критерий Коши сходимости последовательностей
Последовательность { xn } называют последовательностью Коши или фундаментальной, если
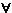   0 0 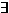 N такой, что для N такой, что для 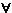 n, m n, m  N: | xn - xm | N: | xn - xm |  
| ( 4.4.1 ) |
( здесь центр интервала длиной 2  помещен в точку xm,m
помещен в точку xm,m  N , см. рис 4.4.1 )
N , см. рис 4.4.1 )
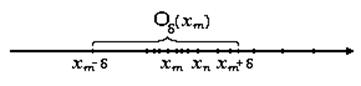
Рис. 4.4.1
Теорема 4.4.1( Критерий Коши ) Для того, чтобы последовательность{ xn }сходилась, необходимо и достаточно чтобы она была фундаментальной.
Доказательство.Необходимость. Пусть xn 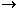 a при n
a при n 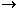
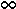 . Тогда для любого
. Тогда для любого 
 0 существует N, что для любых n, m
0 существует N, что для любых n, m  Nвыполняется | xn - a |
Nвыполняется | xn - a | 
 / 2, | xm - a |
/ 2, | xm - a | 
 / 2. Рассмотрим цепочку неравенств
/ 2. Рассмотрим цепочку неравенств
| xn - xm | = | ( xn - a ) + ( a - xm ) |  | xn - a | + | xm - a |
| xn - a | + | xm - a | 


 / 2
/ 2 
 / 2
/ 2
n≥N m≥N
что означает, что { xn } фундаментальна (| xn - xm | 
 - условие фундаментальности).
- условие фундаментальности).
Достаточность. По теореме Больцано-Вейерштрасса (из всякой последовательности можно выделить сходящуюся подпоследовательность) из последовательности { xn } можно выделить подпослеловательность, сходящуюся к некоторому числу a. Докажем, что и вся последовательность сходится к числу a.
Возьмем любое 
 0, тогда найдется номер N( из фундаментальности { xn } ), что для всех n, m
0, тогда найдется номер N( из фундаментальности { xn } ), что для всех n, m  N выполняется | xn - xm |
N выполняется | xn - xm | 
 . В виду сходимости подпоследовательности (из { xn })
. В виду сходимости подпоследовательности (из { xn })
xnk 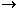 a при k
a при k 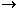
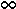 по взятому
по взятому 
 0 найдется номер k0, такой, что (номер элемента в подпоследовательности) nk0
0 найдется номер k0, такой, что (номер элемента в подпоследовательности) nk0  N и | xnk0 - a |
N и | xnk0 - a | 
 / 2 . Тогда для любого n
/ 2 . Тогда для любого n  N :
N :
| xn - a | = | xn - xm + xm - a | =[ xm = xnk0 ]  | xn - xm | + | xnk0 - a |
| xn - xm | + | xnk0 - a | 
 ,
,
что означает сходимость последовательности { xn } к числу a.
/* Пояснения к последнему абзацу :)
Так как подпоследовательностьxnk сходится к a, начиная с некоторого номера N1 все члены xnkÎ { 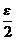 - окрестности точки a}, а так как последовательность xn- фундаментальная, то начиная с некоторого номера N2 все члены xnотстоят от членов xnk меньше, чем на
- окрестности точки a}, а так как последовательность xn- фундаментальная, то начиная с некоторого номера N2 все члены xnотстоят от членов xnk меньше, чем на 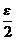 . Следовательно, начиная с номера N = max (N1,N2) все члены последовательности xnÎ {e- окрестности точки a}, а это и означает, что
. Следовательно, начиная с номера N = max (N1,N2) все члены последовательности xnÎ {e- окрестности точки a}, а это и означает, что 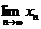 = a, что и требовалось доказать. */
= a, что и требовалось доказать. */
Замечание:в лекции в пункте «достаточность» Афонин говорил лишь о том, что | xn - a | 
 при n≥N, но вдруг внезапно он попросит это доказать?
при n≥N, но вдруг внезапно он попросит это доказать?
Дата добавления: 2018-05-12; просмотров: 329; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
