Последовательности независимых испытаний. Формулы

Бернулли, Лапласа, Пуассона

Конечное число испытаний называются независимыми, если их исходы представляют собой события, независимые в совокупности. Иными словами, вероятность наступления некоторого события в каждом из испытаний не зависит от исходов других испытаний.

Испытаниями Бернулли называются повторные независимые испытания, в каждом из которых нас интересуют только два исхода (будем называть их «успех» и «неудача»), вероятности которых постоянны в каждом испытании.

Например, при многократном подбрасывании монеты (за успех принимаем выпадение герба, за неудачу – выпадение решки) вероятность успеха p 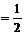, вероятность неудачи q = 1 – p 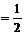. При многократном подбрасывании игральной кости (за успех принимаем выпадение на верхней грани «1», за неудачу – выпадение любого другого числа («2» или «3», или «4», или «5», или «6»)) вероятность успеха p , вероятность неудачи q = 1 – p .

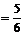Если производится n независимых испытаний в одинаковых условиях, в каждом из которых с одной и той же вероятностью p может произойти событие A, то вероятность P_n(m) того, что в этих n испытаниях событие A произойдет ровно m раз, определяется по формуле Бернулли.

1 Обычно при решении задач формула Бернулли применяется, если число экспериментов невелико ( .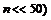

Формула Бернулли

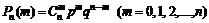, (10)

где q = 1 – p – вероятность непоявления события A в каждом из испытаний;

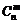– число сочетаний из n элементов по m, которое вычисляется по формуле:

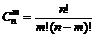, где .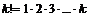

Примечание. Сочетаниями (или неупорядоченными выборками без возвращения) из п различных элементов по т называются множества, содержащие т элементов из числа п заданных, и которые отличаются хотя бы одним элементом. Число сочетаний из п элементов по т обозначают: ).

2 Очевидно, что при больших значениях n пользоваться формулой Бернулли затруднительно, так как придется вычислять значения факториалов больших чисел и возводить в большую степень числа, близкие к нулю (0 < p < 1). В этом случае можно использовать асимптотические формулы Лапласа, дающие тем лучшее приближенное значение P_n(m) и P_n(k₁£ m £ k₂), чем больше n.

Локальная формула Лапласа.Если вероятность p появления события A в каждом испытании постоянна и отлична от нуля и единицы (0 < p < 1), то вероятность того, что событие A появится в серии из n испытаний ровно m раз приближенно равна

, (11)

где , .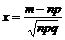

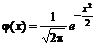(В приложении A приведена таблица значений функции 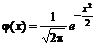, соответствующих положительным значениям аргумента.)

Функция j(x) является четной функцией, то есть j(– x) = j(x), для всех 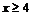принимается j( x) = 0.

Интегральная формула Лапласа.Если вероятность p наступления события A в каждом испытании постоянна и отлична от нуля и единицы (0 < p < 1), то вероятность того, что событие A появится в серии из n испытаний от k₁ до k₂ раз, приближенно равна

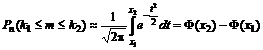, (12)

где , ,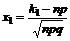

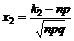В приложении Б приведена таблица значений функции ЛапласаF(x).

Функция F(x) нечетна, то есть F(– x) = – F(x). При x > 5 можно принять F(x) = 0,5.

3 Пусть число экспериментов Бернулли велико ( 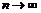), а вероятность наступления события A в каждом испытании очень мала ( ), тогда вероятность того, что событие A появится в серии из n испытаний ровно m раз, приближенно равна

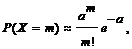(13)

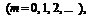где .

Приведем таблицу, с помощью которой, можно определить формулу при решении задачи.

Таблица 1 – Условия применения формул при испытаниях Бернулли

Число испытаний, n
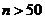
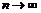
Вероятность наступления события А, р(А)	0 < p < 1	0 < p < 1
Формула	Бернулли	Лапласа	Пуассона

Наивероятнейшее число m₀ наступлений события A в серии из n испытаний, в каждом из которых оно может наступить с вероятностью p, определяется из двойного неравенства (m₀– целое)

np – q £ m₀£ np + p.

Пример 10Предприятие для изучения потребительских предпочтений на товар в случайном порядке рассылает анкеты по адресам (почтовый опрос). Вероятность того, что заполненные потребителями анкеты «возвратятся» на предприятие, составляет 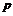. Определить:

а) какова вероятность того, что из отправленных анкет «возвратятся» не более 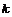анкет;

б) найдите наиболее вероятное число анкет, «возвратившихся» на предприятие, и соответствующую этому значению вероятность.

Рассмотрим решение задачи для трех постановок:

Задача	n	P	k
Задача 1	10	0,4	3
Задача 2	100	0,4	40
Задача 3	200	0,05	2

Определим случайный эксперимент Е: предприятие для изучения потребительских предпочтений на товар в случайном порядке рассылает анкеты по адресам.

Задача 1

Решение.

Условие задачи можно рассматривать как серию из n = 10 независимых испытаний, состоящих в рассылке анкет, в каждом из которых с вероятностью 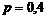может осуществиться событие A = {отправленная анкета «возвратится» на предприятие}. Вероятность того, что отправленная анкета «не возвратится» на предприятие, равна q = 1 – 0,4 = 0,6.

а) Определим событие B = {из 10 отправленных анкет менее 4 «возвратятся» на предприятие}.

Так как число испытаний невелико для вычисления вероятности события B = {из 10 отправленных анкет менее 4 «возвратятся» на предприятие} можно воспользоваться точной формулой Бернулли и теоремой сложения вероятностей несовместных событий:

Р(В) = + + + ;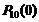

;

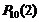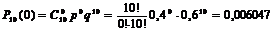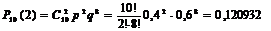Р(В) = 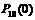+ + 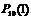+ 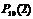= 0,006047+ 0,040311+ 0,120932+ 0,214991 = 0,38228.

б) Определим наиболее вероятное число анкет, «возвратившихся» на предприятие по формуле

np – q £ m₀ £ np + p.

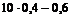£ m₀ £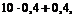

3,4 £ m₀ £ 4,4.

Наивероятнейшее число m₀ = 4.

C = {из 10 отправленных анкет ровно 4 «возвратятся» на предприятие}.

Для определения вероятности события С воспользуемся формулой Бернулли

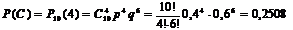Ответ: а) вероятность того, что из 10 отправленных анкет менее 4 «возвратятся» на предприятие, равна 0,382; б) наиболее вероятное число отправленных анкет, которые «возвратятся» на предприятие, составит 4, соответствующая этому числу вероятность 0,251.

Задача 2

Решение.

а) Условие задачи можно рассматривать как серию из n = 100 независимых испытаний, состоящих в рассылке анкет, в каждом из которых с вероятностью 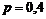может осуществиться событие A = {отправленная анкета «возвратится» на предприятие}. Вероятность того, что посланная анкета «не возвратится» на предприятие, равна q = 1 – 0,4 = 0,6.

а) Так как число испытаний достаточно велико для вычисления вероятностей события B = {из 100 отправленных анкет менее 40 «возвратятся» на предприятие} можно воспользоваться приближённой интегральной формулой Муавра-Лапласа при n = 100; p = 0,4; q = 1 – 0,4 = 0,6; k₁= 0; k₂= 40:

;

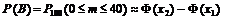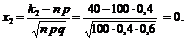
По таблицам значений функции 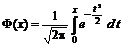находим F (–8,165) = = – 0,5, F (0) = 0,0.

Таким образом,

б) Определим наиболее вероятное число анкет, которые «возвратятся» на предприятие по формуле

np – q £ m₀ £ np + p.

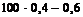£ m₀ £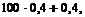

39,4 £ m₀ £ 40,4.

Наивероятнейшее число m₀ = 40.

Так как число испытаний достаточно велико для вычисления вероятности события C = {из 100 разосланных анкет ровно 40 «возвратятся» на предприятие} можно воспользоваться приближённой локальной формулой Муавра-Лапласа при n = 100; p = 0,4; q = 0,6; m = 40:

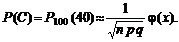
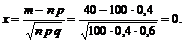
По таблицам значений функции 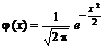находим j (0) = 0,3989.

Ответ: а) вероятность того, что из 100 отправленных анкет не более 40 «возвратятся» на предприятие, равна 0,5; б) наиболее вероятное число отправленных анкет, которые «возвратятся» на предприятие, составит 40, соответствующая этому числу вероятность 0,0814.

Задача 3

Решение.

Условие задачи можно рассматривать как серию из n = 200 независимых испытаний, состоящих в рассылке анкет, в каждом из которых с вероятностью 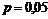может осуществиться событие A = {отправленная анкета «возвратится» на предприятие}. Вероятность того, что посланная анкета «не возвратится» на предприятие, равна q = 1 – 0,05 = 0,95.

В данном случае для вычисления вероятностей воспользуемся приближенной формулой Пуассона с параметром a = np, так какчисло испытаний n = 200достаточно велико, а вероятность появления события в каждом испытании p = 0,05очень мала (p < 0,1), то есть в каждом отдельном опыте событие A появляется крайне редко:

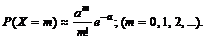
Таблица значений функции 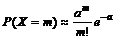приведена в приложении В.

a = np = .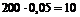

а) Определим событие В = {не более двух анкет «возвратятся» на предприятие, то есть или 0, или 1, или 2}.

Вероятность события В

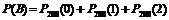
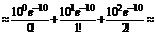
= 0,0028.

б)

Определим наиболее вероятное число анкет, «возвратившихся» на предприятие, по формуле

np – q £ m₀ £ np + p,

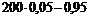£ m₀ £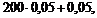

9,05 £ m₀ £ 10,05.

Наивероятнейшее число m₀ = 10.

Определим событие С = {10 анкет «возвратятся» на предприятие}.

Вероятность события С

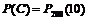
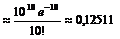Ответ: а) вероятность того, что из 200 отправленных анкет не более 2 «возвратятся» на предприятие, равна 0,002769; б) наиболее вероятное число отправленных анкет, которые «возвратятся» на предприятие, составит 10, соответствующая этому числу вероятность 0,12511.

Вопросы для самоконтроля

1 Какие испытания называются независимыми? Приведите примеры.

2 Какие испытания называются испытаниями Бернулли? Приведите примеры.

3 Что определяется по формуле Бернулли?

4 При каких условиях применяется формула Пуассона?

5 При каких условиях применяются формулы Myaвpa-Лапласа?

6 Что определяется по локальной формуле Муавра-Лапласа?

7 Что определяется по интегральной формуле Муавра-Лапласа?

8 Как определить наивероятнейшее число наступлений события A в серии из n испытаний?

СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

Дата добавления: 2018-05-12; просмотров: 316; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 234 5 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!