Теоремы сложения и умножения вероятностей
Теоремы сложения вероятностей
В общем случае теорема сложения вероятностей для двух событий A и B определяется по формуле
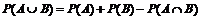 . (2)
. (2)
Если события A и B – несовместны, то есть AÇB = Æ, P(AÇB) = 0, то
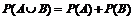 . (3)
. (3)
Теорема сложения вероятностей для трех событий A, B, C может быть записана следующим образом:

Если события A, B, C – попарно несовместны, то
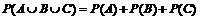 .
.
Согласно аксиоме 3 для счетного числа несовместных событий A1, A2, A3,…
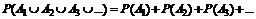
Пример 6Из трех карточек с цифрами 1, 4, 5 произвольным образом выбирают 2 и укладывают на стол в порядке их появления. Предполагая, что все возможные исходы данного опыта равновероятны, найти вероятность того, что:
а) полученное таким образом число будет или четное, или меньше 50;
б) полученное таким образом число будет или четное, или нечетное.
Решение. Пространство элементарных исходов данного эксперимента может быть представлено следующим образом: W = {14, 15, 41, 45, 51, 54}, (n = 6).
а) Определим событие A = {полученное случайным образом число будет или четное, или меньше 50}.
Определим события B = {полученное случайным образом число будет четное}; C = {полученное случайным образом число будет меньше 50}, которые совместны.
Таким образом, для определения вероятности события A можем воспользоваться теоремой сложения вероятностей для двух совместных событий P(А) = 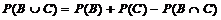 .
.
|
|
|
Все элементарные исходы данного пространства W равновероятны. Таким образом, для определения вероятностей событий В и С можем воспользоваться классическим методом определения вероятности. Выпишем исходы, благоприятные интересующих нас событиям:
B = {14, 54}, (m = 2), тогда P(B) = 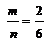 ;
;
С = {14, 15, 41, 45}, (m = 4), P(С) = 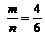 ,
,
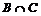 ={полученное случайным образом число будет четное и меньше 50},
={полученное случайным образом число будет четное и меньше 50}, 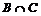 ={14}, (m = 1), P(
={14}, (m = 1), P( 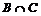 ) =
) = 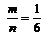 .
.
Тогда вероятность события А:
P(А) = 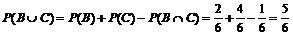 = 0,833.
= 0,833.
б) Определим событие D = {полученное случайным образом число будет или четное, или нечетное}.
Определим события B = {полученное случайным образом число будет четное}; Е = {полученное случайным образом число будет нечетное}, которые несовместны.
Таким образом, для определения вероятности события D можем воспользоваться теоремой сложения вероятностей для двух несовместных событий P(D) = 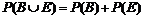 .
.
Все элементарные исходы данного пространства W равновероятны. Таким образом, для определения вероятностей событий В и Е можем воспользоваться классическим методом определения вероятности. Выпишем исходы, благоприятные интересующих нас событиям:
|
|
|
B = {14, 54}, (m = 2), тогда P(B) = 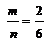 ;
;
Е = {15, 41, 45, 51}, (m = 4), P(Е) = 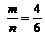 ,
,
Тогда вероятность события D:
P(D) =  .
.
Условная вероятность. Теорема умножения вероятностей
Рассмотрим вероятностный эксперимент Е. Пусть в пространстве 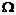 определены некоторые случайные события А, В, С, … и их вероятности. Предположим, что в ходе нашего эксперимента Е событие А уже произошло. В данном эксперименте появление события А может каким-то образом изменить вероятности появления событий, связанных (зависимых) с ним.
определены некоторые случайные события А, В, С, … и их вероятности. Предположим, что в ходе нашего эксперимента Е событие А уже произошло. В данном эксперименте появление события А может каким-то образом изменить вероятности появления событий, связанных (зависимых) с ним.
Событие В называется зависимым от события А, если появление (или не появление) события А изменяет вероятность появления события В. Событие В называется независимым от события А, если появление (или не появление) события А не изменяет вероятность появления события В.
Рассмотрим два произвольных события A и B, причем P(B) ¹ 0.
Условной вероятностью события A при условии B (обозначается P(A|B)) называется вероятность события A, вычисленная при условии, что событие B уже произошло. По определению
P(A | B) = P(A Ç B)/P(B). (4)
Вычисление условных вероятностей – это, по существу, переход в новое, урезанное заданным условием B пространство элементарных событий. Вероятности элементарных событий P(wi) (wiÎB) пропорциональны исходным. Для соблюдения условия нормировки в новом пространстве элементарных событий они делятся на P(B).
|
|
|
Аналогично
P(B | A) = P(A Ç B)/P(A) (5)
в случае, если P(A) ¹ 0.
Теорема умножения вероятностей: Вероятность произведения двух событий равна произведению вероятностей одного из них на условную вероятность другого, вычисленную при условии, что первое имело.
P(AÇB) = P(B)P(A|B) = P(A)P(B|A) (6)
Для произвольного числа n событий A1, A2,… An теорема умножения вероятностей имеет вид
P(A1 Ç A2 Ç … Ç An) = P(A1)P(A2|A1) … P(An|A1 Ç A2 Ç … Ç Аn-1),
то есть вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события произошли.
Пример 7Студент пришел на зачет, зная из 30 вопросов только 20. Какова вероятность того, что он сдаст зачет, если для этого необходимо ответить хотя бы на два вопроса из трех, содержащихся в билете?
|
|
|
Решение. Обозначим события:
А = {студент сдаст зачет};
В = {студент ответит на три вопроса из трех, содержащихся в билете};
С = {студент ответит на два вопроса из трех, содержащихся в билете}.
Вспомогательные события:
В1 ={студент ответит на первый вопрос, содержащийся в билете};
В2 = {студент ответит на второй вопрос, содержащийся в билете};
В3 = {студент ответит на третий вопрос, содержащийся в билете}.
События В и С несовместны. Событие А произойдет, если произойдет одно из событий В или С.
По теореме сложения вероятностей несовместных событий P(А) = 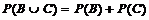 .
.
Определим вероятности событий В и С.
Событие В : В = В1 ÇВ2 ÇВ3.
Вероятность события В определим по формуле
Р(В) = Р(В1) Р(В2 | В1) Р(В3 | В2Ç В1 ),
где Р(В1) = 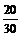 (всего 30 вопросов, из которых 20 студент знает);
(всего 30 вопросов, из которых 20 студент знает);
Р(В2| В1)=  (всего осталось 29 вопросов, из них 19 студент знает);
(всего осталось 29 вопросов, из них 19 студент знает);
Р(В3| В2 Ç В1) = 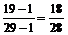 (всего осталось 28 вопросов, из них 18 студент знает).
(всего осталось 28 вопросов, из них 18 студент знает).
По теореме умножения вероятностей зависимых событий
P(В) = P(В1) P(В2| В1) P(В3| В2Ç В1) = 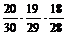 =
= 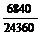 = 0,281.
= 0,281.
Вероятность события С определим, используя теорему сложения вероятностей несовместных событий.
Р(С) = Р(С1) + Р(С2) + Р(С3),
где С1 = {студент ответит на первый и второй вопросы, а на третий не ответит};
С2 = {студент ответит на первый и третий вопросы, а на второй не ответит};
С3= {студент ответит на второй и третий вопросы, а на первый не ответит}.
Событие С1 : С1 = В1 ÇВ2 Ç 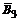 . Событие С2 : С2 =
. Событие С2 : С2 =  1 ÇВ2 Ç В3.
1 ÇВ2 Ç В3.
Событие С3 : С3 = В1 Ç 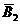 Ç В3..
Ç В3..
P(С1) = P(В1) P(В2| В1) P( 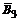 | В2Ç В1) =
| В2Ç В1) = 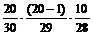 =
= 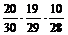 =
=
= 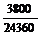 = 0,156.
= 0,156.
P(С2) = P(В1) P( 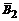 | В1) P(В3|
| В1) P(В3| 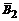 Ç В1) =
Ç В1) = 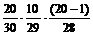 =
= 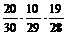 =
=
= 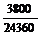 = 0,156.
= 0,156.
P(С3) = P(  ) P(В2|
) P(В2|  ) P(В3| В2Ç
) P(В3| В2Ç  ) =
) = 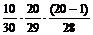 =
= 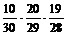 =
=
= 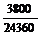 = 0,156.
= 0,156.
Р(С) = Р(С1) + Р(С2) + Р(С3) = 0,156 + 0,156 +0,156 = 0,468.
По теореме сложения вероятностей несовместных событий P(А) = 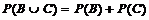 = 0,281 + 0,468 = 0,749.
= 0,281 + 0,468 = 0,749.
Ответ. Вероятность того, что студент сдаст зачет равна 0,749.
Независимые события
Два события A и B называются независимыми, если
P(AÇB) = P(A)P(B). (7)
Для пояснения естественности такого определения вернемся к теореме умножения вероятностей (6) и установим, в каких ситуациях из нее следует (7). Очевидно, что это может быть тогда, когда условная вероятность P(A|B) равна соответствующей безусловной вероятности события А: P(A|B) = P(A), то есть когда вероятность события А не зависит от того, произошло событие В или нет. (Аналогично, P(B|A) = P(B)).
В основе независимости событий лежит их физическая независимость, состоящая в том, что множества факторов, влияющих на исход эксперимента и обусловливающих появление этих событий, не пересекаются или почти не пересекаются.
События A1, A2,…, Anназываютсянезависимыми в совокупности, если вероятность каждого из этих событий не зависит от появления любого числа остальных событий.
Теорема умножения вероятностей для независимых в совокупности событий A1, A2,…, An имеет вид
P(A1 Ç A2 Ç … Ç An) = P(A1)P(A2) … P(An).
Пример 8При изготовлении изделие проходит три основные независимые операции. Вероятность того, что изделие успешно пройдет первую операцию равна 0,9, вторую – 0,95, третью – 0,8. Найти вероятность того, что:
а) изделие окажется стандартным;
б) изделие окажется нестандартным.
Решение. Обозначим события:
Ai = {i-ю операцию изделие прошло без брака}, i = 1, 2, 3;
B = {изделие окажется стандартным};
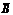 = {изделие окажется нестандартным}.
= {изделие окажется нестандартным}.
Согласно условию: вероятность события A1 равна P(A1) = 0,9, вероятность события A2равна P(A2) = 0,95, вероятность события A3 равна P(A3) = 0,8.
Тогда вероятности противоположных событий:
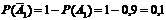 ,
,  ,
,
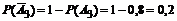 .
.
Определим все варианты данного случайного эксперимента и соответствующие вероятности, применяя теорему умножения вероятностей независимых событий:
| События | Вероятности |

| 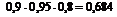
|
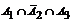
| 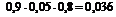
|
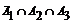
| 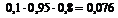
|
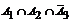
| 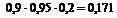
|
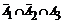
| 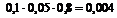
|
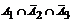
| 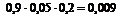
|
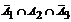
| 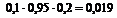
|

| 
|
| Итого 1 |
а) По теореме умножения вероятностей независимых событий
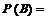
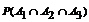 =
= 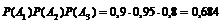 .
.
б) Применяя теорему сложения вероятностей несовместных событий и теорему умножения вероятностей независимых событий, получим
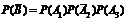
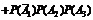
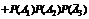 + +
+ + 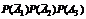 +
+ 
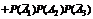 +
+ 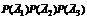 = 0,036 + 0,076 + 0,171 + 0,004 + 0,009 + 0,019 + 0,001 = 0,316.
= 0,036 + 0,076 + 0,171 + 0,004 + 0,009 + 0,019 + 0,001 = 0,316.
События B = {изделие окажется стандартным} и 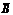 = {изделие окажется нестандартным} являются противоположными, то есть
= {изделие окажется нестандартным} являются противоположными, то есть 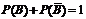 ,
,
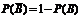 = 1 – 0,684= 0,316.
= 1 – 0,684= 0,316.
Ответ. Вероятность того, что:
а) изделие окажется стандартным равна 0,684;
б) изделие окажется нестандартным равна 0,316.
Дата добавления: 2018-05-12; просмотров: 310; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
