Решение для цилиндра круглого поперечного сечения.
Уравнение контура С записывается в виде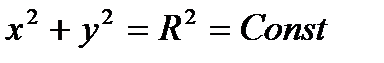 
Поэтому мы получаем частный вид уравнения (134)
 , 
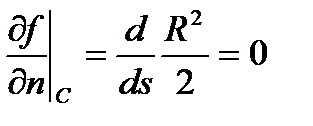
| (138) |
Из (138) следует решение 
. В случае, если какая-то точка цилиндра закреплена, то из условия 
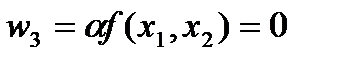следует равенство нулю функции кручения.
Следовательно
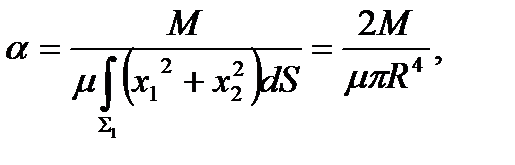
| (139) |
| (140) |
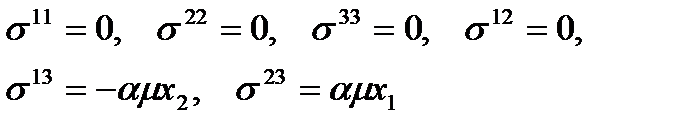
| (141) |
Откуда максимальное касательное напряжение достигается на внешнем радиусе
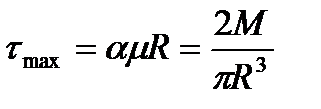
| (142) |
Метод Сен-Венана
Рассмотрим условия на границе цилиндра (132). Есть способ заменить производную по нормали от функции кручения на производную по контуру как в правой части от сопряженной функции.
Функция кручения гармоническая функция. Рассмотрим гармоническую функцию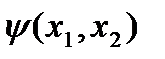 
сопряженную по условиям Коши-Римана
| (143) |
Из этих равенств с учетом (133) производная функции кручения меняется:
| (144) |
Откуда получаем уже задачу не Неймана, а Дирихле для сопряженной функции
| (145) |
Определим теперь аналитическую функцию
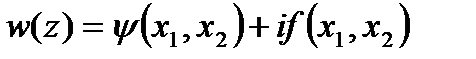
| (146) |
Если уравнение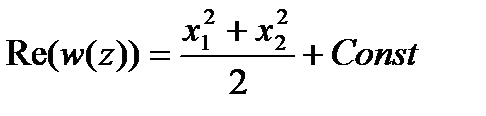 
выражает некую замкнутую кривую, то ее можно принять за контур поперечного сечения, при этом 
будет определять депланацию – смещение точек поперечного сечения вдоль ортогональной ему оси.
Решение для цилиндра эллиптического сечения.
Рассмотрим функцию
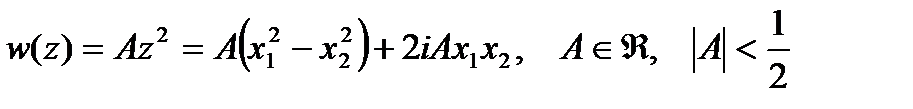
| (147) |
Положим
| (148) |
Тогда уравнение
| (149) |
Определит уравнение эллипса 
с осями
| (150) |
Откуда следует, что функция
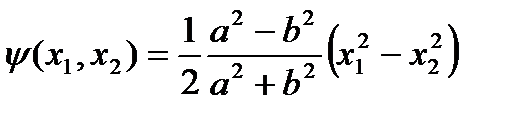
| (151) |
дает решение задачи о кручении цилиндрического стержня с поперечным сечением, ограниченным эллипсом .
|
|
|
Мембранная аналогия
Лекция 9. Изгиб балки.
Принцип Сен-Венана.
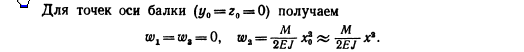
Лекция 10. Плоские задачи теории упругости.
Плоское деформированное состояние.
Где реализуется плоское деформированное состояние.
Цилиндрическое тело.
Плоское напряженное состояние.
Где реализуется плоское напряженное состояние.
Тонкая пластина.
Лекция 11. Формулы Гурса и Колосова-Мусхелишвили.
Введем обозначение
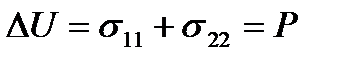
| (152) |
Ясно, что функция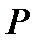 
гармоническая, так как
| (153) |
Тогда
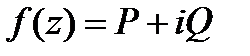
| (154) |
Аналитическая функция комплексного переменного.
Положим
| (155) |
Тогда
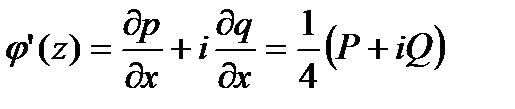Формула Гурса
| (156) |
Покажем, что для бигармонической функции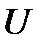 
выражение 
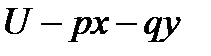является гармонической функцией. Учитывая условия Коши-Римана для 
и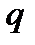 
, получаем
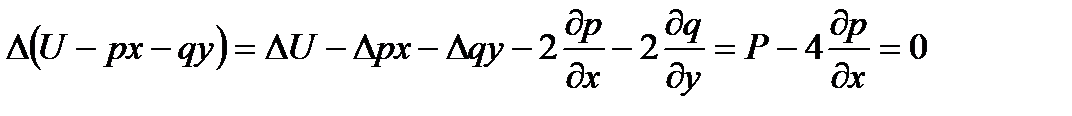
| (157) |
То есть
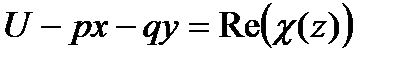
| (158) |
или
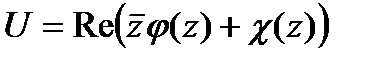
| (159) |
Откуда следует Формула Гурса
| (160) |
Выражений напряжений через функцию Эри мы получаем следующие равенства
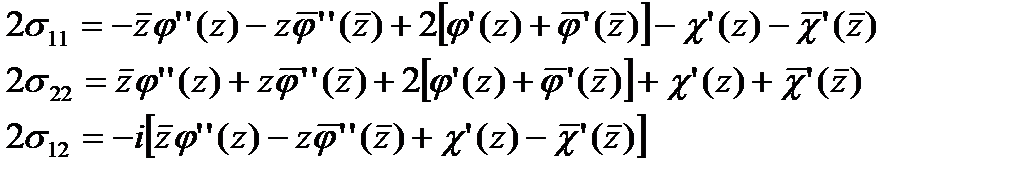
| (161) |
Комбинируя эти уравнения получаем
Формулы Колосова-Мусхелишвили для напряжений
| (162) |
Это уравнения в напряжениях. Из закона Гука мы получаем уравнения в перемещениях.
|
|
|
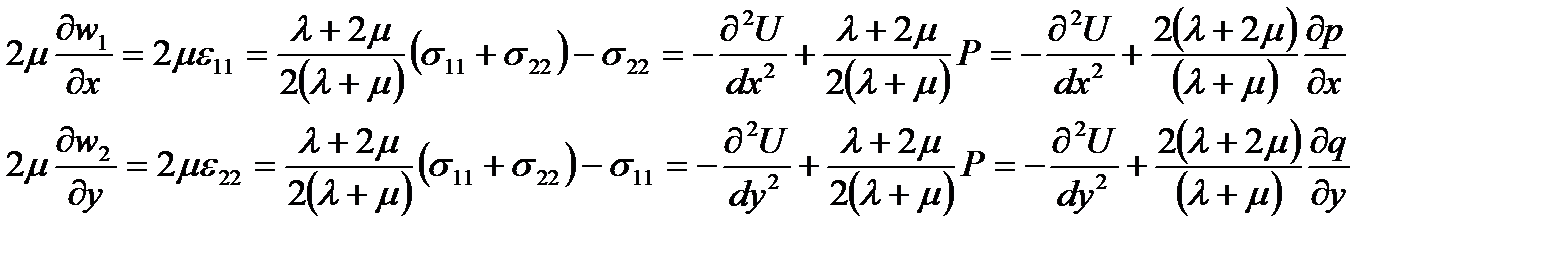
| (163) |
Интегрируя, получаем
| (164) |
Учитывая (164) в соотношениях закона Гука для 
, получаем
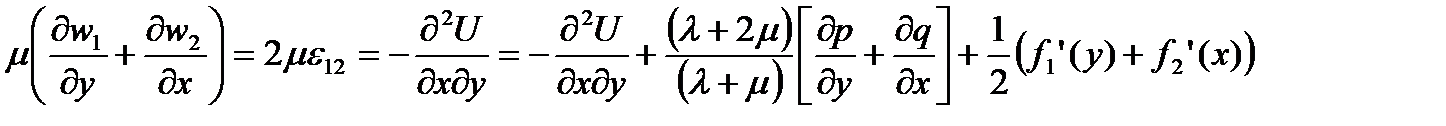
| (165) |
Откуда следует, что
| (166) |
Для любых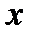 
и 
, а значит 
, откуда
| (167) |
Что определяет лишь жесткое смещение и вращение тела в пространстве. Далее мы полагаем эти слагаемые равными нулю.
Получаемформулы Лява
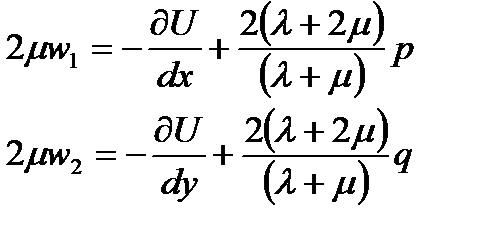
| (168) |
Удобно представить плоское поле перемещений в виде
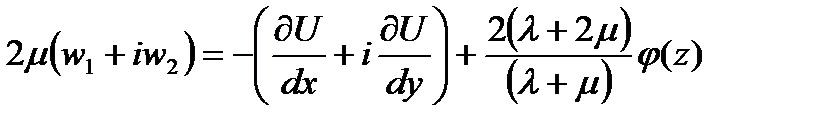
| (169) |
Откуда, учитывая формулы Гурса (160), получаем
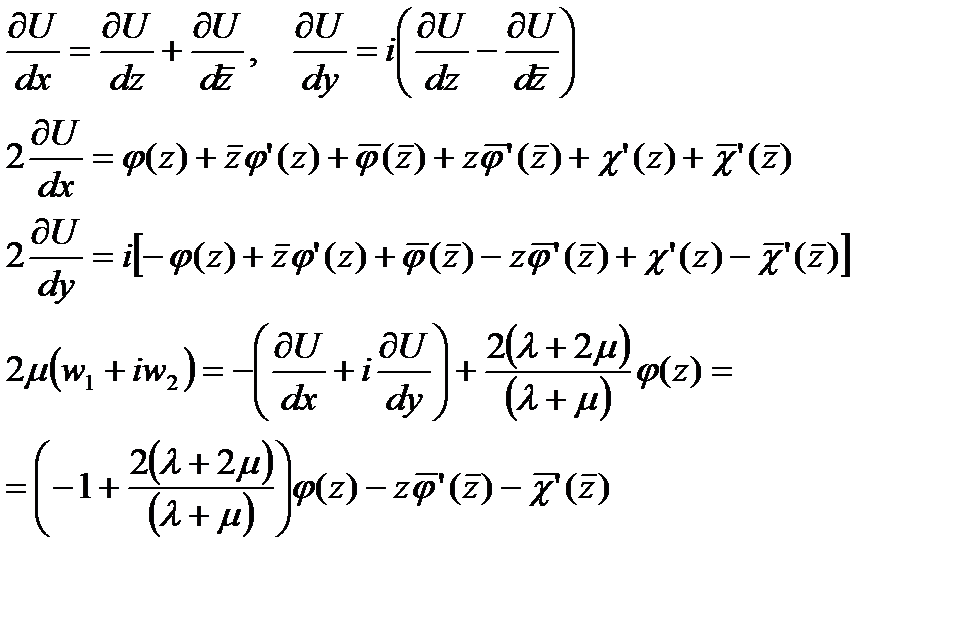
| (170) |
В итоге у нас получилась
Дата добавления: 2018-05-12; просмотров: 325; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!