Пара - напряженияи деформации.
Исходя из уравнения (28) одной переменной будет тензор деформаций 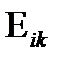 как реакция материала на введение напряжений
как реакция материала на введение напряжений 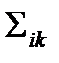 .
.
Пара – температура и энтропия.
Реакцией материала на введение абсолютной температуры 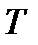 , как скалярной величины, задающей меру нагретости тела, будет введение плотности скорости притока энтропии извне
, как скалярной величины, задающей меру нагретости тела, будет введение плотности скорости притока энтропии извне 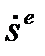 как равной плотности скорости притока тепла извне
как равной плотности скорости притока тепла извне 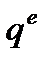 с учетом температуры
с учетом температуры 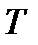 как интегрирующего множителя:
как интегрирующего множителя:
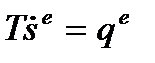
| (29) |
Второе начало термодинамики.
Второй закон термодинамики постулирует соотношение (29), а также условие 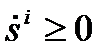
Где  - плотность производства энтропии внутри системы, участвующая в задании функции состояния системы – энтропии
- плотность производства энтропии внутри системы, участвующая в задании функции состояния системы – энтропии
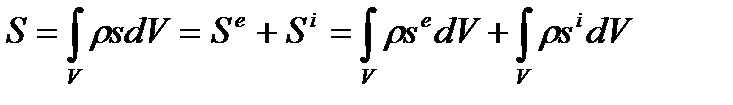
| (30) |
где 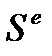 - приток энтропии извне, связан с притоком массы или тепла к системе, а
- приток энтропии извне, связан с притоком массы или тепла к системе, а
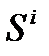 - производство энтропии внутри системы. То есть, можно записать равенства
- производство энтропии внутри системы. То есть, можно записать равенства
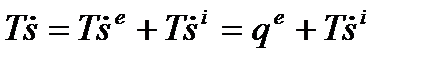
| (31) |
Из условий 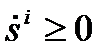 и
и 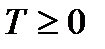 следует оценка
следует оценка
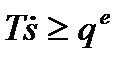
| (32) |
Таким образом, рассматривая часть притока энергии системы в виде тепловой энергии, мы заменяем скорость притока тепла 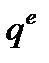 температурой
температурой 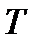 и плотностью скорости изменения энтропии
и плотностью скорости изменения энтропии 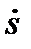 .
.
Выразим 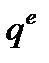 из уравнения притока тепла (27)
из уравнения притока тепла (27)
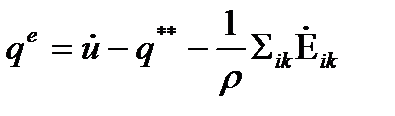
| (33) |
с учетом неравенства (32) получаем неравенство диссипации или
Неравенство Клаузиуса-Дюгема
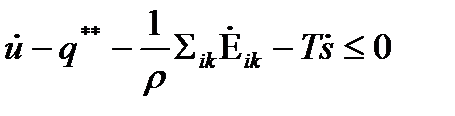
| (34) |
Из неравенства диссипации (неравенства К.Д.) следует, что вторым параметром состояния системы, переменной для внутренней энергии, будет плотность энтропии 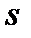 .
.
|
|
|
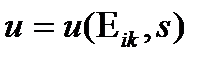
| (35) |
Далее до определенного момента, для простоты, будем полагать отсутствие нетепловых источников энергии
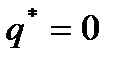
| (36) |
Тогда неравенство К.Д. будет проще
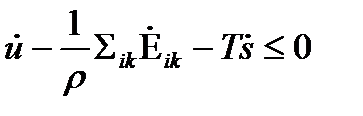
| (37) |
Свободная энергия
Удобно выбрать другой термодинамический потенциал – свободная энергия 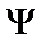 (свободная энергия Гельмгольца).
(свободная энергия Гельмгольца).
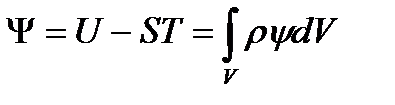 , где , где  – плотность свободной энергии – плотность свободной энергии
| (38) |
Для него параметрами состояния системы являются температура и деформация
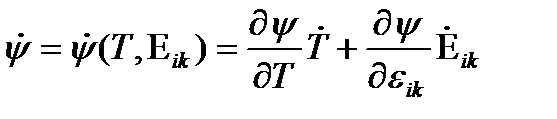
| (39) |
Тогда неравенство К.Д. (37) сводится к виду
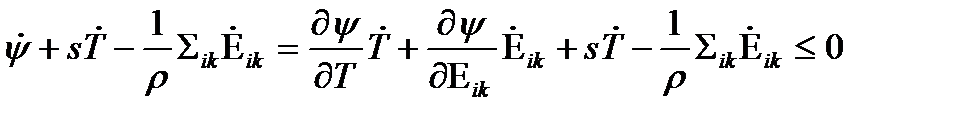
| (40) |
Группируя множите при скоростях изменения параметров состояния
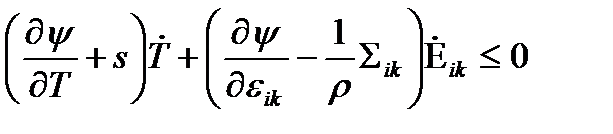
| (41) |
Получаем, что при условии произвольности знаков скорости изменения каждого из параметров состояния обязаны выполняться следующие равенства, являющиеся определяющими соотношениями для нашей среды:
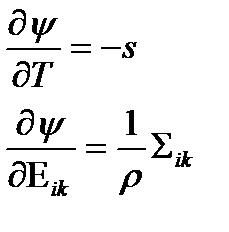 при при 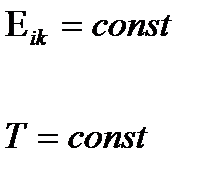
| (42) |
Лекция 3. Нелинейная теория упругости.
Энергетические пары.
Только в случае симметричного тензора напряжений 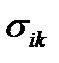 плотность мощности работы внутренних поверхностных сил с обратным знаком равна свертке тензора напряжений с тензором скоростей деформаций
плотность мощности работы внутренних поверхностных сил с обратным знаком равна свертке тензора напряжений с тензором скоростей деформаций  , который только в случае малых деформаций равен полной производной по времени от тензора малых деформаций
, который только в случае малых деформаций равен полной производной по времени от тензора малых деформаций 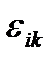 :
:
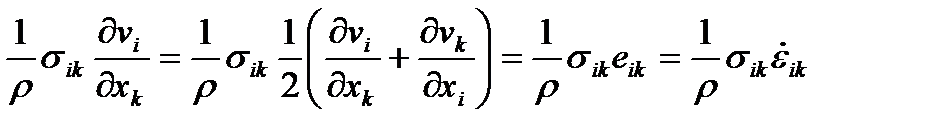
| (43) |
В более общем случае еще предстоит представить свертку 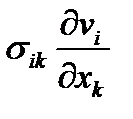 в виде пары тензоров
в виде пары тензоров 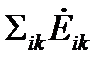 , чтобы выполнялось равенство для плотности мощности работы внутренних поверхностных сил:
, чтобы выполнялось равенство для плотности мощности работы внутренних поверхностных сил:
|
|
|
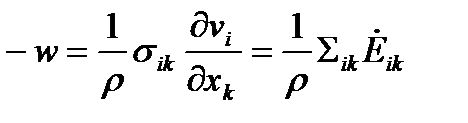
| (44) |
Пара тензоров 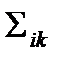 и
и 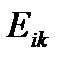 называется [Ошибка!Источник ссылки не найден.]энергетической парой, связанной соотношением
называется [Ошибка!Источник ссылки не найден.]энергетической парой, связанной соотношением
 в актуальной конфигурации или
в актуальной конфигурации или 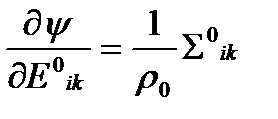 в отсчетной.
в отсчетной.
Рассмотрим методику получения энергетической пары для равенства Ошибка! Источник ссылки не найден..
Рассмотрим закон движения частиц среды 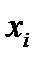 в текущий, актуальный момент времени
в текущий, актуальный момент времени 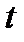 :
:
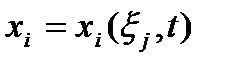 , , 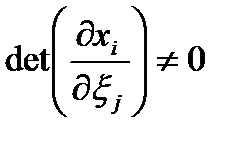 , и обратный , и обратный 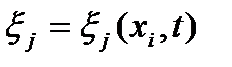 , , 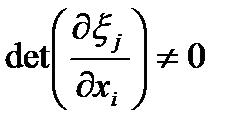 , ,
| (45) |
где 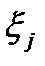 координаты частицы в начальный момент времени, в отсчетной конфигурации.
координаты частицы в начальный момент времени, в отсчетной конфигурации.
Воспользуемся двумя утверждениями.
Первое:
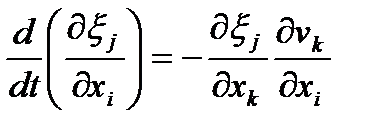 , так как , так как
| (46) |
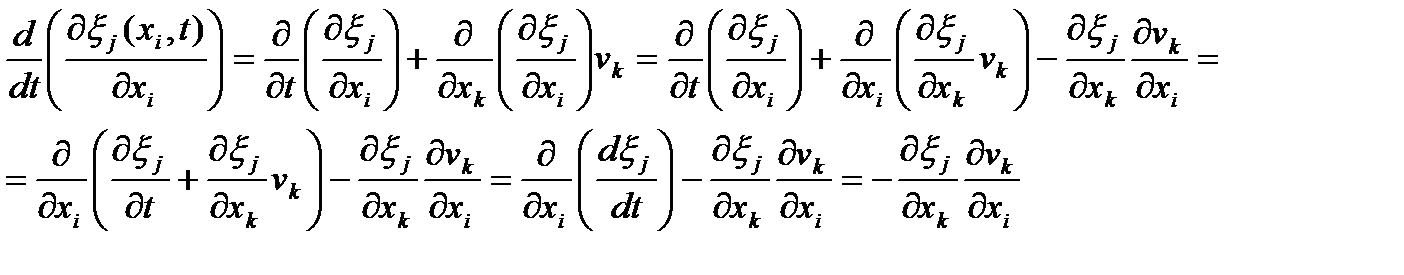 , откуда , откуда
| (47) |
 , ,
| (48) |
Второе:
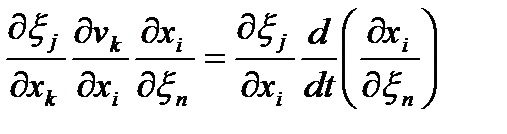 , так как , так как
| (49) |
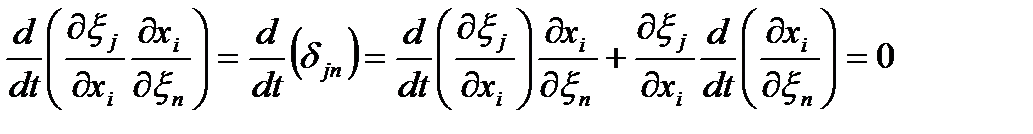 , с учетом (46), откуда, домножив(49)на , с учетом (46), откуда, домножив(49)на 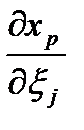 и и 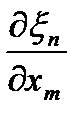 с обеих сторон и, заменив затем pнаk, m на i, получаем: с обеих сторон и, заменив затем pнаk, m на i, получаем:
| (50) |
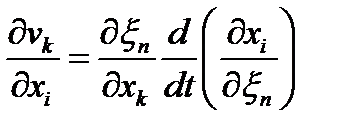 , ,
| (51) |
На основании (51) из (44) мы получаем
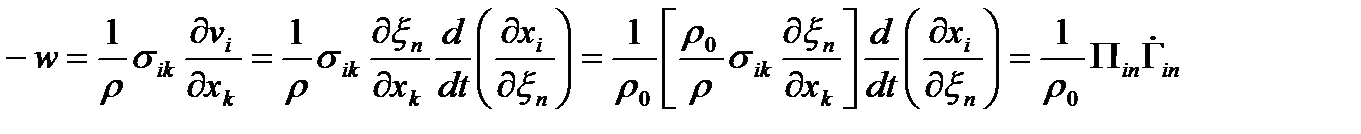
| (52) |
Где
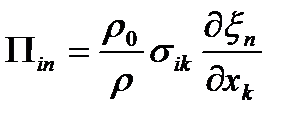 тензор напряжений Пиолы, тензор напряжений Пиолы,
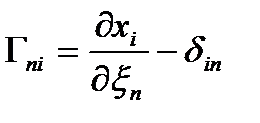 тензор-градиент деформаций. тензор-градиент деформаций.
| (53) |
Смысл тензора напряжений Пиолы.
Рассмотрим объем параллелепипеда, натянутого на тройку векторов 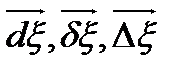 в начальной (отсчетной) конфигурации и в текущей (актуальной) конфигурации на тройке векторов
в начальной (отсчетной) конфигурации и в текущей (актуальной) конфигурации на тройке векторов 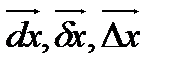
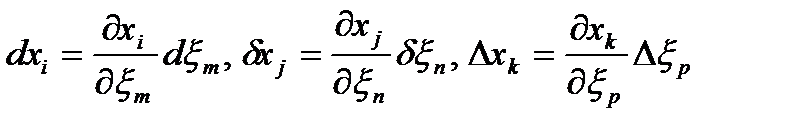 , ,
| (54) |
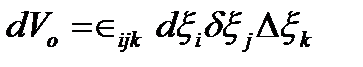 , , 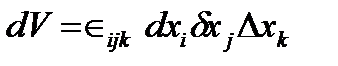 , где , где 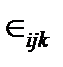 - тензор Леви-Чивиты в ортонормированном базисе. - тензор Леви-Чивиты в ортонормированном базисе.
| (55) |
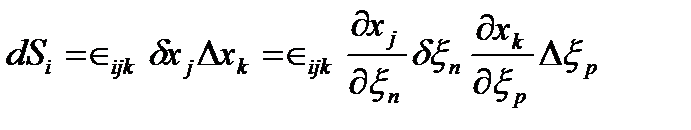 , ,
| (56) |
Домножим(56) на 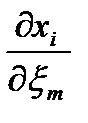 , получим
, получим
|
|
|
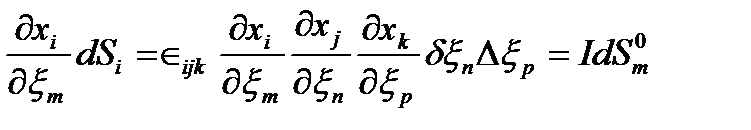 , ,
| (57) |
Откуда
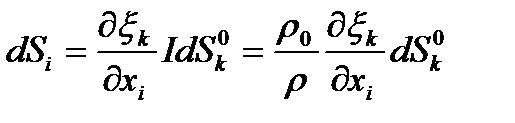 , ,
| (58) |
Рассмотрим силу в текущем (актуальном) состоянии усилие на площадке
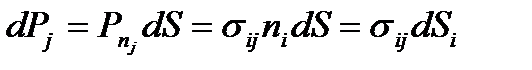
| (59) |
Подставим соотношение (58) и получим
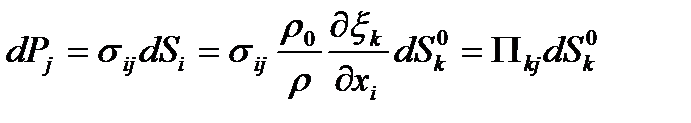
| (60) |
То есть тензор Пиолы 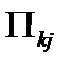 в отсчетной конфигурации играет ту же роль, что и тензор Коши
в отсчетной конфигурации играет ту же роль, что и тензор Коши 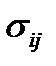 в актуальной.
в актуальной.
Симметричные тензоры деформации.
Тензор-градиент деформаций (тензор дисторсии) несимметричен. Если мы изначально воспользуемся симметрией тензора напряжений, то можно получить симметричный тензор деформации исходя из представления плотности мощности работы внутренних сил в виде
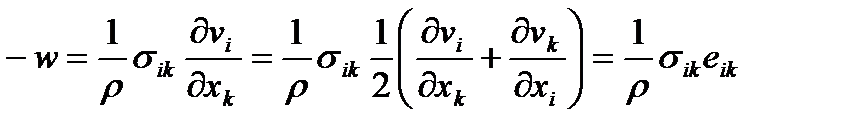
| (61) |
Отсчетная конфигурация.
Воспользуемся соотношением (51) и получим из (44)
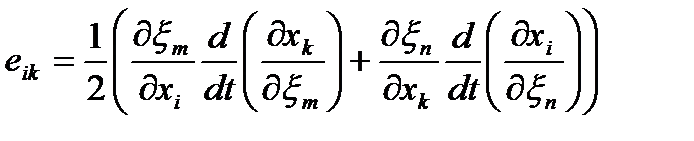
| (62) |
Домножив(72)на 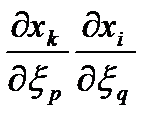 получим
получим
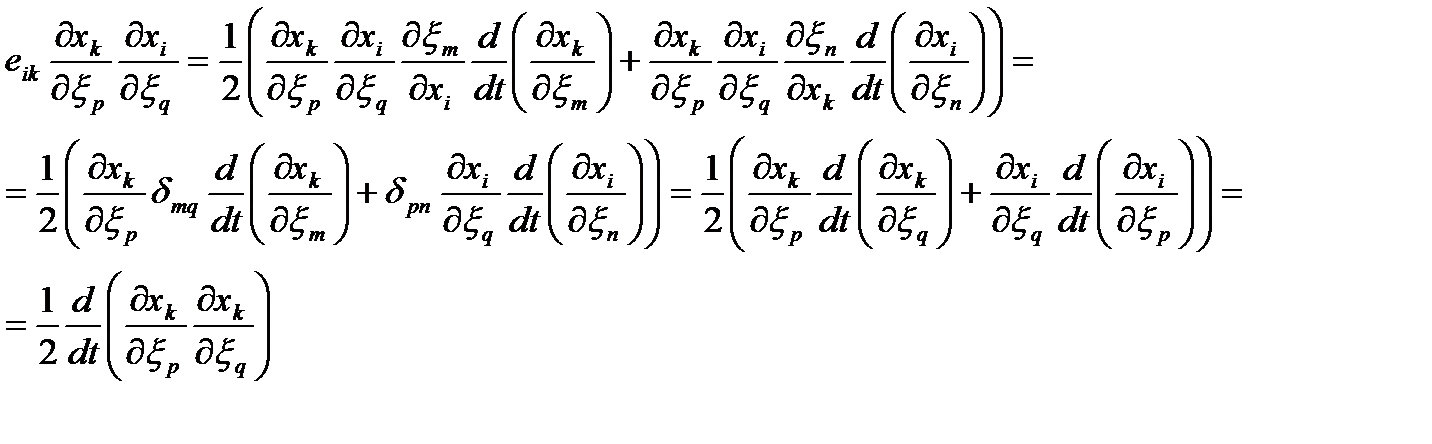
| (63) |
Откуда выражаем тензор скоростей деформаций и получаем
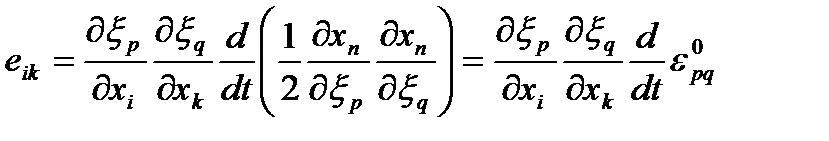
| (64) |
Теперь плотность мощности поверхностных сил можно представить в виде

| (65) |
Где
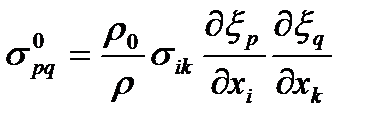 тензор напряжений Кирхгофа, тензор напряжений Кирхгофа,
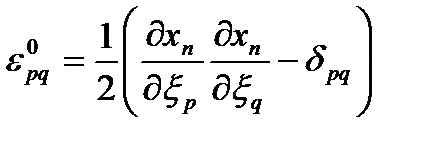 тензор деформаций Грина тензор деформаций Грина
| (66) |
Актуальная конфигурация.
Аналогично отсчетной конфигурации, но используя уже не (51), а уравнение (48) получим из (44)
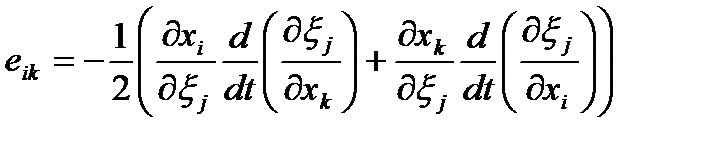
| (67) |
Используя аналогичные приемы, получаем
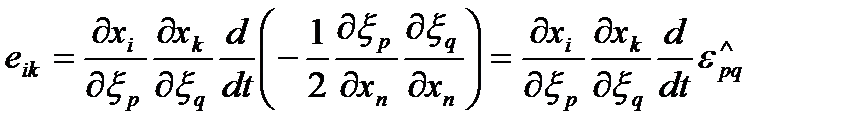
| (68) |
Теперь плотность мощности поверхностных сил можно представить в виде
|
|
|
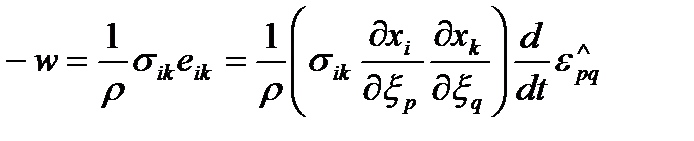
| (69) |
Где
 тензор напряжений в актуальной конфигурации, тензор напряжений в актуальной конфигурации,
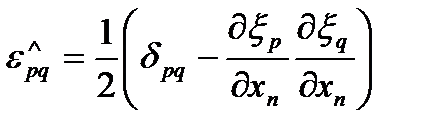 тензор деформаций Альманси тензор деформаций Альманси
| (70) |
В изотермическом случае мы имеем изОшибка! Источник ссылки не найден.соотношение, связывающее напряжения и деформации
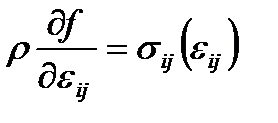 при при 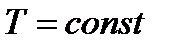
| (71) |
В случае, аргумент этого выражения представляет собой симметричный тензор второго ранга, то возможно существенное упрощение этой произвольной зависимости.
Дата добавления: 2018-05-12; просмотров: 298; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
