Замена переменной в определенном интеграле
Материалы по теме: интеграл, функция, определенный интеграл, лекция по высшей математики, формула, высшая математика
При вычислении определенных интегралов с использованием формулы Ньютона-Лейбница предпочтительно жестко не разграничивать этапы решения задачи (нахождение первообразной подынтегральной функции, нахождение приращения первообразной). Такой подход, использующий, в частности, формулы замены переменной и интегрирования по частям для определенного интеграла, обычно позволяет упростить запись решения.
ТЕОРЕМА. Пусть функция φ(t) имеет непрерывную производную на отрезке [α,β], а=φ(α), в=φ(β) и функция f(х) непрерывна в каждой точке х вида х=φ(t), где t[α,β].
Тогда справедливо следующее равенство:

Эта формула носит название формулы замены переменной в определенном интеграле.
Подобно тому, как это было в случае неопределенного интеграла, использование замены переменной позволяет упростить интеграл, приблизив его к табличному (табличным). При этом в отличие от неопределенного интеграла в данном случае нет необходимости возвращаться к исходной переменной интегрирования. Достаточно лишь найти пределы интегрирования α и β по новой переменной t как решение относительно переменной t уравнений φ(t)=а и φ(t)=в. На практике, выполняя замену переменной, часто начинают с того, что указывают выражение t=ψ(х) новой переменной через старую. В этом случае нахождение пределов интегрирования по переменной t упрощается: α=ψ(а), β=ψ(в).
|
|
|
Пример 19. Вычислить 
Положим t=2-х2. Тогда dt=d(2-х2)=(2-х2)'dx=-2xdx и xdx=-  dt. Если х=0, то t=2-02=2, и если х=1, то t=2-12=1. Следовательно:
dt. Если х=0, то t=2-02=2, и если х=1, то t=2-12=1. Следовательно:

Пример 20. Вычислить 
Воспользуемся заменой переменной  . Тогда
. Тогда 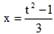 и
и  . Если х=0, то t=1 и, если х=5, то t=4. Выполняя замену, получим:
. Если х=0, то t=1 и, если х=5, то t=4. Выполняя замену, получим:

Пример 21. Вычислить 
Положим t=ex. Тогда x=lnt, dx=dt/t и, если x=ln2, то t=2, если х=ln3, то t=3. Выполняя замену, получаем:
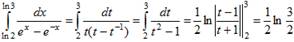
Несобственные интегралы.
Несобственный интеграл – это «продвинутый» определенный интеграл, и на самом деле сложностей с ними не так уж и много, к тому же у несобственного интеграла есть очень хороший геометрический смысл.
Определённый интеграл называется несобственным, если выполняется, по крайней мере, одно из следующих условий:
Предел a или b (или оба предела) являются бесконечными;
Функция f(x) имеет одну или несколько точек разрыва внутри отрезка [a, b].
Приближённое вычисление определённых интегралов
Рассмотрим задачу о приближённом нахождении значения определённого интеграла

Относительно подынтегральной функции  мы будем предполагать, что она непрерывна на отрезке интегрирования, а также, когда это понадобится, что она имеет на этом отрезке производные до некоторого порядка.
мы будем предполагать, что она непрерывна на отрезке интегрирования, а также, когда это понадобится, что она имеет на этом отрезке производные до некоторого порядка.
|
|
|
Вычислять значение интеграла 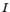 мы будем по значениям функции
мы будем по значениям функции  в некоторых точках отрезка
в некоторых точках отрезка  . Эти значения
. Эти значения  мы будем предполагать известными, то есть предполагать, что у нас есть некоторый эффективный способ вычисления значений функции с любой требуемой точностью. Формулы, позволяющие по известным значениям
мы будем предполагать известными, то есть предполагать, что у нас есть некоторый эффективный способ вычисления значений функции с любой требуемой точностью. Формулы, позволяющие по известным значениям 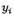 приближённо определить значение
приближённо определить значение 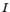 , называются квадратурными формулами.
, называются квадратурными формулами.
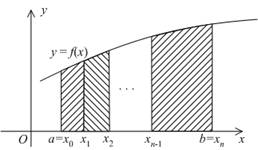
Для наглядности мы будем прибегать к геометрической интерпретации смысла определённого интеграла, как площади некоторой криволинейной трапеции, в случае функции 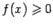 . Следует, однако, иметь в виду, что квадратурные формулы, которые мы будем получать, имеют смысл для функций, принимающих значения произвольного знака.
. Следует, однако, иметь в виду, что квадратурные формулы, которые мы будем получать, имеют смысл для функций, принимающих значения произвольного знака.
При 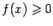 вычислить интеграл
вычислить интеграл 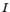 значит найти площадь под графиком
значит найти площадь под графиком 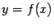 , расположенную над отрезком
, расположенную над отрезком 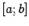 . Естественной идеей является следующее построение: разобьём отрезок на части точками деления
. Естественной идеей является следующее построение: разобьём отрезок на части точками деления  и положим
и положим 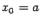 и
и 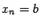 (см. определение значения определённого интеграла). Тогда разбиение отрезка
(см. определение значения определённого интеграла). Тогда разбиение отрезка 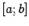 состоит из отрезков
состоит из отрезков 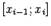 при
при 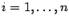 . Вместо площади под графиком, равной
. Вместо площади под графиком, равной 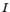 , будем приближённо находить суммарную площадь узких полосок, лежащих над отрезками разбиения
, будем приближённо находить суммарную площадь узких полосок, лежащих над отрезками разбиения 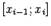 (см. рис.).
(см. рис.).
|
|
|
Рис.5.1.
21. –
Длина дуги кривой.
Пусть задана кривая 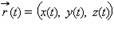 Тогда длина ее участка, ограниченного значениями t = α и t = β выражается формулой
Тогда длина ее участка, ограниченного значениями t = α и t = β выражается формулой
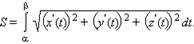
В частности, длина плоской кривой, задаваемой на координатной плоскости OXY уравнением y = f (x), a ≤ x ≤ b, выражается формулой
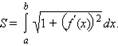
Дата добавления: 2018-05-12; просмотров: 298; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
