Одноканальная СМО с ожиданием, без ограничений на вместимость накопителя

Система массового обслуживания имеет один канал. Входящий поток заявок на обслуживание - простейший поток с интенсивностью λ. Интенсивность потока обслуживания равна μ (т. е. в среднем непрерывно занятый канал будет выдавать μ обслуженных заявок). Длительность обслуживания - случайная величина, подчиненная показательному закону распределения. Поток обслуживании является простейшим пуассоновским потоком событий. Заявка, поступившая в момент, когда канал занят, становится в очередь и ожидает обслуживания.

Рассмотреним одноканальную СМО с ожиданием без ограничения на вместимость блока ожидания (т. е.N"∞) Остальные условия функционирования СМО остаются без изменений.

Рассмотрим количество требований в системе в момент времени (T+h), h>0, интервал времени очень малой продолжительности.

Перенесем P_n влево и разделим уравнение на h. Получим выражение

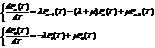(4.12)

n>0, h→0.

Стационарный режим функционирования данной СМО существует при t→∞ для любого n = 0, 1, 2, ... и когда λ<μ. Система алгебраических уравнений, описывающих работу СМО при t→∞ для любого n = 0, 1, 2, ... _. имеет вид

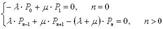.(4.13)

Решение данной системы уравнений имеет вид

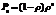, n = 0, 1, 2, ...              (4.14)

где 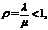 - интенсивность обслуживания (коэффициент загрузки канала обслуживания).

Характеристики одноканальной СМО с ожиданием, без ограничения на длину очереди, следующие:

· среднее число находящихся в системе клиентов (заявок) на обслуживание:

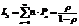   (4.15);

· средняя продолжительность пребывания клиента в системе:

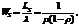   (4.16);

· среднее число клиентов в очереди на обслуживании:

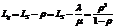        (4.17);

· средняя продолжительность пребывания клиента в очереди:

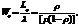   (4.18).

Пример 4.2. Специализированный пост диагностики представляет собой одноканальную СМО. Поток автомобилей, прибывающих на диагностику, распределен по закону Пуассона и имеет интенсивность λ= 0,85 (автомобиля в час). Время диагностики автомобиля распределено по показательному зако­ну и в среднем равно 1,05 час. . Пусть рассматриваемый пост диагностики располагает неограниченным количеством площадок для стоянки прибывающих на обслуживание автомобилей, т. е. длина очереди не ограничена.

Требуется определить вероятностные характеристики поста диагностики, работающего в стационарном режиме, то есть требуется определить финальные значения следующих вероятностных характеристик:

1. вероятности состояний системы (поста диагностики);

2. среднее число автомобилей, находящихся в системе (на обслуживании и в очереди);

3. среднюю продолжительность пребывания автомобиля в системе (на обслуживании и в очереди);

4. среднее число автомобилей в очереди на обслуживании;

5. среднюю продолжительность пребывания автомобиля в очереди.

Решение

1. Параметр потока обслуживания μ и приведенная интенсивность потока автомобилей ρ определены в примере 4.2: μ=0,952; ρ =0,893.

2. Вычислим предельные вероятности системы по формулам (ψ= ρ)

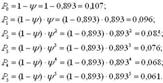 и т.д.

Следует отметить, что P₀(t) определяет долю времени, в течение которого пост диагностики вынужденно бездействует (простаива­ет). В нашем примере она составляет 10,7%, так как P₀(t) = 0,107.

3. Среднее число автомобилей, находящихся в системе (на об­служивании и в очереди) (ψ= ρ):

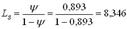 ед.

4. Средняя продолжительность пребывания клиента в системе:

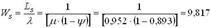час.

5. Среднее число автомобилей в очереди на обслуживание:

.

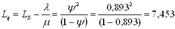6. Средняя продолжительность пребывания автомобиля в очереди:

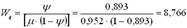 час.

7. Относительная пропускная способность системы: q = 1 т. е. каждая заявка, пришедшая в систему, будет обслужена. 8. Абсолютная пропускная способность:

.

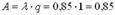Следует отметить, что предприятие, осуществляющее диагностику автомобилей, прежде всего интересует количество клиентов, которое посетит пост диагностики при снятии ограничения на длину очереди.

Допустим, в первоначальном варианте количество мест для стоянки прибывающих автомобилей было равно трем (см. пример 4.2). Частота т возникновения ситуаций, когда прибывающий на пост диагностики автомобиль не имеет возможности присоединиться к очереди: .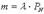

В нашем примере при N = 3 + 1 = 4 и ψ= 0,893

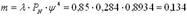 автомобиля в час

При 12-часовом режиме работы поста диагностики это эквива­лентно тому, что пост диагностики в среднем за смену (день) будет терять 12 • 0,134 = 1,6 автомобиля.

Снятие ограничения на длину очереди позволяет увеличить ко­личество обслуженных клиентов в нашем примере в среднем на 1,6 автомобиля за смену (12ч. работы) поста диагностики. Ясно, что ре­шение относительно расширения площади для стоянки автомоби­лей, прибывающих на пост диагностики, должно основываться на оценке экономического ущерба, который обусловлен потерей клиентов при наличии всего трех мест для стоянки этих автомобилей.

46.Дайте определение и приведите основные соотношения для моделирования замкнутых систем массового обслуживания

Основное отличие разомкнутой системы от замкнутой состоит в том, что в разомкнутой системе интенсивность поступления требований - характеристика источника требований. В замкнутой системе потенциальное число требований яв-ся величиной постоянной. После обслу­живания требования оно возвращается в источник. В замкнутой систе­ме интенсивность поступления требований Х- характеристика конкретного объекта, поступающего в систему.

Например, обслуживается машинный парк, состоящий из N машин, бригадой R механиков (N > R), причем каждая машина может обслуживаться только одним механиком. Здесь машины яв-ся источниками требований (заявок на обслуживание), а механики - обслуживающими каналами. Неисправная машина после обслуживания используется по своему прямому назначению и становится потенциальным источником возникновения требований на обслуживание. Очевидно, что интенсивность λ  зависит от того, сколько машин в данный момент находится в эксплуатации (N - k) и сколько машин обслуживается или стоит в очереди, ожидая обслуживания (k).

В рассматриваемой модели емкость источника требований следует считать ограниченной. Входящий поток требований исходит из ограниченного числа эксплуатируемых машин (N - k), которые в случайные моменты времени выходят из строя и требуют обслуживания. При этом каждая машина из (N - k) находится в эксплуатации и генерирует пуассоновский поток требований с интенсивностью X независимо от других объектов; общий (суммарный) входящий поток имеет интенсивность (N-k)*λ. Требование, поступившее в систему в момент, когда свободен хотя бы один канал, немедленно идет на обслуживание. Если требование застает все каналы занятыми обслуживанием других требований, то оно не покидает систему, а становится в очередь и ждет, пока один из каналов не станет свободным.

Таким образом, в замкнутой системе массового обслуживания входящий поток требований формируется из выходящего.

Состояние S_k системы характеризуется общим числом требований, находящихся на обслуживании и в очереди, равным k. Для рассматриваемой замкнутой системы, очевидно, k = 0, 1, 2, ... , N. При этом если система находится в состоянии S_k , то число объектов, находящихся в эксплуатации, равно (N - k).

Если λ - интенсивность потока требований в расчете на одну машину, то:

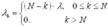;     (5.41)

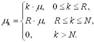
Система алгебраических уравнений, описывающих работу замкнутой СМО в стационарном режиме, выглядит следующим образом:

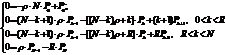(5.42)

Решая данную систему, находим вероятность k-гo состояния:

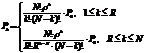(5.43)

Величина P₀ определяется из условия нормирования   полученных результатов по формулам (2.2.41) для P_k , k = 0, 1, 2, ... , N. Определим следующие вероятностные характеристики системы:

среднее число требований в очереди на обслуживание:

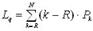;                  (5.44)

среднее число требований, находящихся в системе (на обслуживании и в очереди)

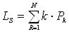        (5.45)

среднее число механиков (каналов), «простаивающих» из-за отсутствия работы

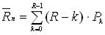;            (5.46)

коэффициент простоя обслуживаемого объекта (машины) в очереди

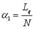; (5.47)

коэффициент использования объектов (машин)

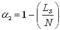;           (5.48)

коэффициент простоя обслуживающих каналов (механиков)

; (5.49)

среднее время ожидания обслуживания (время ожидания обслуживания в очереди)

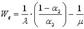. (5.50)

48.Проанализируйте процесс построения модели системы

 

 

49.Дайте определение и опишите сущность имитационного моделирования систем

Особым видом моделей яв-ся имитационные модели. Имитационное моделирование проводится в тех случаях, когда исследователь имеет дело с такими математическими моделями, которые не позволяют заранее вычислить или предсказать результат. В этом случае для предсказания поведения реальной сложной системы необходим эксперимент, имитация на модели при заданных исходных параметрах. Имитация представляет собой численный метод проведения на ЭВМ экспериментов с математическими моделями, описывающими поведение сложной системы в течение заданного или формируемого периода времени. Поведение компонентов сложной системы и их взаимодействие в имитационной модели чаще всего описывается набором алгоритмов, реализуемых на некотором языке моделирования. Термин «имитационная модель» используют в том случае, когда речь идет о проведении численных расчетов и в частности о получении статистической выборки на математической модели, например, для оценки вероятностных характеристик некоторых выходных параметров. Моделирование на системном уровне применяется в системном анализе для проведения расчетов характеристик будущей системы. При построении имитационной модели исследователя, прежде всего, интересует возможность вычисления некоторого функционала, заданного на множестве реализаций процесса функционирования изучаемой системы. Наиболее важным для исследователя функционалом яв-ся показатель эффективности системы. Имитируя различные реальные ситуации на модели, исследователь получает возможность решения таких задач как оценка эффективности тех или иных принципов управления системой, сравнение вариантов структурных схем, определение степени влияния изменений параметров системы и начальных условий на показатель эффективности системы. Примерами расчетов на имитационных моделях также могут служить вычисления характеристик производительности, надежности, качества функционирования и т.п., которые необходимо определить как функции внутренних и внешних параметров системы.

Ответственный этап создания имитационной модели представляет собой этап составления формального описания объекта моделирования сложной системы. Цель этапа - получение исследователем формального представления алгоритмов поведения компонентов сложной системы и отражение вопросов взаимодействия между собой этих компонентов. При составлении формального описания модели исследователь использует тот или иной язык формализации. В зависимости от сложности объекта моделирования и внешней среды могут использоваться три вида формализации: аппроксимация явлений функциональными зависимостями, алгоритмическое описание происходящих в системе процессов, комбинированное представление в виде формул и алгоритмических записей.

Сложность системы и вероятностный характер процессов, происходящих в объекте исследования, свидетельствуют о том, что для определения выходных характеристик системы необходимо использовать стохастические модели. Вероятностный характер процессов, происходящих в сложных системах, приводит к невозможности аппроксимации явлений функциональными зависимостями. Доминирующим методом при моделировании сложных систем яв-ся способ алгоритмического описания происходящих в системе процессов.

Отметим еще одну особенность, которую необходимо учитывать при моделировании процесса функционирования сложной системы. В социотехнических системах люди решают часть задач из общей последовательности задач, решаемых системой, например, задачи управления, принятия решения и т.п. Следовательно, они принципиально не устранимы из системы и должны быть представлены в модели системы как ее элементы. Однако учет так называемого «человеческого фактора» имеет принципиальные сложности. При выполнении человеком производственных операций требуется учитывать квалификацию конкретного исполнителя, его опыт и стаж работы. Необходимо также иметь в виду, что на качество выполняемых процедур могут оказывать влияние состояние его здоровья, эмоционально-психологический настрой и прочие факторы, которые практически не удается формализовать при составлении модели. Поэтому в моделях принимают определенного рода допущения, приводящие к упрощению модели, к решению задачи «в среднем», т.е. задают некоторые средние характеристики выполнения человеком своих функций и при данных значениях проводят расчеты модели. Для того, чтобы учесть возможные отклонения в процессе выполнения операций различными исполнителями, необходимо проводить анализ чувствительности модели

 

52.Опишите основные этапы процесса формализации и алгоритмизации процесса функционирования систем

Этапы моделирования систем.Рассмотрим основные этапы моде­лирования системы S, к числу которых относятся: построение кон­цептуальной модели системы и ее формализация; алгоритмизация модели системы и ее машинная реализация; получение и интерпре­тация результатов моделирования системы.

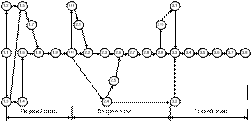 Рис. 8.1. Взаимосвязь этапов моделирования систем

Взаимосвязь перечисленных этапов моделирования систем и их составляющих (подэтапов) может быть представлена в виде сетевого графика, показанного на рис. 8.1. Перечислим эти подэтапы:

1.1 — постановка задачи машинного моделирования системы; 1.2 — анализ задачи моделирования системы; 1.3 — определение требований к исходной информации об объекте моделирования иорганизация ее сбора; 1.4 — выдвижение гипотез и принятие предположений; 1.5 — определение параметров и переменных модели; 1.6 — установление основного содержания модели; 1.7 —обоснование критериев оценки эффективности системы; 1.8 — определение процедур аппроксимации; 1.9 — описание концептуальной модели системы; 1.10 — проверка достоверности концептуальной модели; 1.11 — составление технической документации по первому этапу; 2.1 — построение логической схемы модели; 2.2 — получение математических соотношений; 2.3 — проверка достоверности модели системы; 2.4 — выбор инструментальных средств для моделирования; 2.5 — составление плана выполнения работ по программированию; 2.6 —спецификация и построение схемы программы; 2.7 — верификация и проверка достоверности схемы программы; 2.8 — проведение программирования модели; 2.9 — проверка достоверности программы; 2.10 — составление технической документации по второму этапу; 3.1 — планирование машинного эксперимента с моделью системы; 3.2 — определение требований к вычислительным средствам; 3.3 — проведение рабочих расчетов; 3.4 — анализ результатов моделирования системы; 3.5 — представление результатов моделирования; 3.6 — интерпретация результатов моделирования; 3.7 — подведение итогов моделирования и выдача рекомендаций; 3.8 — составление технической документации по третьему этапу.

Таким образом, процесс моделирования системы S сводится к выполнению перечисленных подэтапов, сгруппированных в виде трех этапов. На этапе построения концептуальной модели М_т и ее формализации проводится исследование моделируемого объекта с точки зрения выделения основных составляющих процесса его функционирования, определяются необходимые аппроксимации и получается обобщенная схема модели системы S, которая преобразуется в машинную модель М_м на втором этапе моделирования путем последовательной алгоритмизации и программирования модели. Последний третий этап моделирования системы сводится к проведению согласно полученному плану рабочих расчетов на ЭВМ с использованием выбранных программно-технических средств, получению и интерпретации результатов моделирования системы S с учетом воздействия внешней среды Е. Очевидно, что при построении модели и ее машинной реализации при получении новой информации возможен пересмотр ранее принятых решений, т. е. процесс моделирования является итерационным. Рассмотрим содержание каждого из этапов более подробно.

 

53.Укажите принципы разработки схем моделирующих алгоритмов

Принципы построениямоделирующих алгоритмов.Процесс функционирования системы S можно рассматривать как последовательную смену ее состояний z=z(z₁(t), z₂{t), ..., z_k{t)) в k-мерном пространстве. Очевидно, что задачей моделирования процесса фукционирования исследуемой системы S является построение функций z, на основе которых можно провести вычисление интересующих характеристик процесса функционирования системы. Для этого должны иметься соотношения, связывающие функции z с переменными, параметрами и временем, а также начальные условия z^o=z(z₁(t_o), z₂(t₀), ..., z_k(t₀)) в момент времени t = t₀.

Рассмотрим процесс функционирования некоторой детерминированной системы S_D, в которой отсутствуют случайные факторы, т. е. вектор состояний такой системы можно определить из (2.3) как z=Φ(z⁰, х, t). Тогда состояние процесса в момент времени t_o+jΔtможет быть однозначно определено из соотношений математической модели по известным начальным условиям. Это позволяет строить моделирующий алгоритм процесса функционирования системы. Для этого преобразуем соотношения модели Z к такому виду, чтобы сделать удобным вычисление z₁ (t + Δt), z₂(t+Δt), ..., z_k(t+Δt) по значениям z_i( 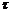), i=l,…, к, где 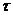≤t. Организуем счетчик системного времени, который в начальный момент показывает время t₀. Для этого момента z_t(t₀)=z_t⁰. Прибавим интервал времени Δt, тогда счетчик будет показывать t_i = t₀ + Δt. Вычислим значения z_i(t₀ + Δt). Затем перейдем к моменту времени t₂ = t₁+Δt и т. д. Если шаг Δt достаточно мал, то таким путем можно получить приближенные значения z.

Рассмотрим процесс функционирования стохастической системы S_R, т. е. системы, на которую оказывают воздействия случайные факторы, т. е. вектор состояний определяется соотношением (2.3). Для такой системы функция состояний процесса z в момент времени 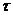≤t и соотношения модели определяют лишь распределение вероятностей для z_i(t + Δt) в момент времени t+Δt. В общем случае иначальные условия z° могут быть случайными, задаваемыми соответствующим распределением вероятностей. При этом структура моделирующего алгоритма для стохастических систем в основном остается прежней. Только вместо состояния z_i (t+Δt) теперь необходимо вычислить распределение вероятностей для возможных состояний. Пусть счетчик системного времени показывает время t₀. В соответствии с заданным распределением вероятностей выбирается z_i°. Далее, исходя из распределения, получается состояние z_i(t_o + Δt) ит. д., пока не будет построена одна из возможных реализаций случайного многомерного процесса z_t(t) в заданном ин­ервале времени [9, 37].

Рассмотренный принцип построения моделирующих алгоритмов называется принципом Δt. Это наиболее универсальный принцип, позволяющий определить последовательные состояния процесса функционирования системы S через заданные интервалы времени Δt. Но с точки зрения затрат машинного времени он иногда оказы-ется неэкономичным.

При рассмотрении процессов функционирования некоторых систем можно обнаружить, что для них характерны два типа состояний: 1) особые, присущие процессу функционирования системы только в некоторые моменты времени (моменты поступления входных управляющих воздействий, возмущений внешней среды и т. п.); 2) неособые, в которых процесс находится все остальное время. Особые состояния характерны еще и тем обстоятельством, что функции состояний z,-(f) в эти моменты времени изменяются скачком, а между особыми состояниями изменение координат z_t(t) происходит плавно и непрерывно или не происходит совсем. Таким образом, следя при моделировании системы Sтолько за ее особыми состояниями в те моменты времени, когда эти состояния имеют место, можно получить информацию, необходимую для построения функций zi(t). Очевидно, для описанного типа систем могут быть построены моделирующие алгоритмы по «принципу особых состояний». Обозначим скачкообразное (релейное) изменение состояния z как δz, а «принцип особых состояний» — как принцип δz.

Например, для системы массового обслуживания (Q-схемы) в качестве особых состояний могут быть выбраны состояния в моменты поступления заявок на обслуживание в прибор П и в моменты окончания обслуживания заявок каналами К, когда состояние системы, оцениваемое числом находящихся в ней заявок, меняется скачком.

Отметим, что характеристики процесса функционирования таких систем с особыми состояниями оцениваются по информации об особых состояниях, а неособые состояния при моделировании не рассматриваются. «Принцип δz» дает возможность для ряда систем существенно уменьшить затраты машинного времени на реализацию моделирующих алгоритмов по сравнению с «принципом Δt». Логика построения моделирующего алгоритма, реализующего «принцип δz», отличается от рассмотренной для «принципа Δt» только тем, что включает в себя процедуру определения момента времени t_s, соответствующего следующему особому состоянию системы S. Для исследования процесса функционирования больших систем рационально использование комбинированного принципа построения моделирующих алгоритмов, сочетающего в себе преимущества каждого из рассмотренных принципов.

Формы представления моделирующих алгоритмов.Удобной формой представления логической структуры моделей процессов функционирования систем и машинных программ является схема. На различных этапах моделирования составляются обобщенные и детальные логические схемы моделирующих алгоритмов, а также схемы программ.

Обобщенная (укрупненная) схема моделирующего алгоритма задает общий порядок действий при моделировании системы без каких-либо уточняющих деталей. Обобщенная схема показывает, что необходимо выполнить на очередном шаге моделирования, например обратиться к датчику случайных чисел.

Детальная схема моделирующего алгоритма содержит уточнения, отсутствующие в обобщенной схеме. Детальная схема показывает не только, что следует выполнить на очередном шаге моделирования системы, но и как это выполнить.

Логическая схема моделирующего алгоритма представляет собой логическую структуру модели процесса функционирования системы S. Логическая схема указывает упорядоченную во времени последовательность логических операций, связанных с решением задачи моделирования.

Схема программы отображает порядок программной реализа­ции моделирующего алгоритма с использованием конкретного ма­тематического обеспечения. Схема программы представляет собой интерпретацию логической схемы моделирующего алгоритма раз­работчиком программы на базе конкретного алгоритмического языка. Различие между этими схемами заключается в том, что логическая схема отражает логическую структуру модели процесса функционирования системы, а схема программы —логику машин­ной реализации модели с использованием конкретных программно-технических средств моделирования.

Логическая схема алгоритма и схема программы могут быть выполнены как в укрупненной, так и в детальной форме. Для начертания этих схем используется набор символов, определяемых ГОСТ 19.701 — 90 (ИСО 5807 — 85) «Единая система программной документации.

 

54.Дайте общую математическую формулировку игровых моделей

Игровые модели дают возможность изучать конфликтные ситуации, в которых каждая из конфликтующих сторон придерживается своих взглядов, и характер поведения каждой из них диктуется личными интересами. Примерами таких систем яв-ся отношения двух или нескольких производителей одинакового товара. Их поведение на рынке обусловлено интересами каждой из сторон. Как правило, эти отношения имеют характер конкурентной борьбы. Принятие решений является одним из важнейших аспектов различных областей жизни и трудовой деятельности людей. Качественные характеристики эффективного решения во многом опираются на количественный научно обоснованный подход, использующий серьезный математический аппарат. Описанная ситуация достаточно часто встречается на практике и ей нетрудно придать ту или иную экономическую интерпретацию. Так, вектор х можно отождествить с ресурсом, а функцию у = у(х) назвать производственной функцией, которая описывает наивыгоднейший для субъекта Б способ использования ресурса. Таким образом, субъекту Б выделяется такое количество ресурса, чтобы его деятельность наилуч­шим образом соответствовала целям субъекта А. Во многих задачах финансово-экономической сферы принятие решения осложняется наличием неопределенности, заключающейся в неполноте информации об окружающей эти задачи среде. Неопределенность такого типа порождается различными объективными причинами, как то: экономическая и финансовая политика государства, реформы в системе налогообложения, курсы валют, инфляция и т.п. Поэтому в задачах подобного рода принятие решения зависит от объективной действительности, называемой в соответствующей математической модели «природой». Сама же математическая модель называется «игрой с природой», а совокупность принципов и методов построения критериев для принятия оптимальных решений составляет раздел математики «Теория игр с природой», или, другими словами, «Теория статистических решений». Таким образом, в игре с природой участвуют два игрока: один из них, обозначим его через А, - лицо, принимающее решение; другой, обозначим его через П, - природа. Игрок А действует осознанно, стремясь принять наиболее выгодное для себя решение, а природа П, в отличие от него , принимает то или иное свое состояние неопределенным образом, не противодействуя злонамеренно игроку А, не преследуя конкретной цели и абсолютно безразлично к результату игры, т.е. природа П, являясь игроком в игре, не является ни противником, ни союзником игрока А.

Пусть игрок А обладает m возможными стратегиями А1,…,Аm, а природа П может находиться в одном из n своих состояний П1,…,Пn. Предполагается обычно, что игрок А в состоянии оценить результаты выбора им каждой из своих стратегий Аi, i=1,…,m, при каждом состоянии природы Пj, j=1,…,n, количественно выражающиеся действительными числами аij.

Эти числа, называемые выигрышами игрока А, можно записать в виде матрицы

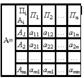размера m x n, строки которой соответствуют стратегиям игрока А, столбцы – состояниям природы П. Задача игрока А состоит в выборе оптимальной стратегии, обеспечивающей ему максимально возможный выигрыш. Поскольку стратегии Аi, i=1,…,m, выбираются игроком А осознанно, а не случайно, то их называют чистыми стратегиями, в отличие от смешанных стратегий, которые в данной статье не рассматриваются. Если в распоряжении игрока А всего одна стратегия А1, т.е. m=1, то проблема выбора им оптимальной стратегии отпадает. Поэтому в дальнейшем целесообразно считать m³2. Если природа П может пребывать только в одном состоянии П1, т.е. n=1, то проблема выбора игроком А оптимальной стратегии превращается в тривиальную: игрок А должен выбрать стратегию Аk такую, что выигрыши аk1³ai1, i=1,…,m. Поэтому будем предполагать , что n³2. Если какая-нибудь k-я строка матрицы А доминируется (в частности, дублируется) другой s-й строкой, т.е. (аk1,…,akn)£(as1,…asn) (в частности, (аk1,…,akn)=(as1,…asn)), то доминируемую (в частности, дублируемую) k-ю строку можно удалить, как строку, определяющую стратегию Аk, заведомо не лучшую стратегии Аs. В результате матрица А упрощается за счет уменьшения числа строк. Таким образом, в дальнейшем будем считать, что матрица А не содержит доминируемых (в частности, дублируемых строк).

Если известны вероятности состояний природы q₁=p(П₁),…,q_n=p(П_n),

которые, очевидно, должны удовлетворять условиям:

(1)

(поскольку события, состоящие в том, что природа П находится в одном из своих состояний П₁,…,П_n, несовместны и составляют полную группу), то говорят о принятии решения «в условиях риска». Если же вероятности, с которыми природа П может находиться в том или ином из своих состояний, неизвестны и отсутствует возможность получения о них какой либо статистической информации, то говорят о принятии решения «в условиях неопределенности». Понятие оптимальности стратегии может определяться различными соображениями, составляющими содержание соответствующих критериев оптимальности.

---

Дата добавления: 2018-05-09; просмотров: 833; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!