Мультипликативный конгруэнтный метод генерации последовательности случайных чисел

⇐ ПредыдущаяСтр 4 из 6Следующая ⇒

мультипликативный конгруэнтный метод задает последовательность неотрицательных целых чисел xj (xj<m), получаемых по формуле:

х_n+1=ах_n(mod m). (2)

на значения накладываются ограничения:

· хо — нечетно;

· а=5^2р+1 (р=0, 1, 2, ...) или a=2^m+3 (m=3, 4, 5, ...) — обе эти записи означают, что младшая цифра а при представлении а в восьмеричной системе счисления должна быть равна 3 или 5 (проще говоря, остаток от деления а/8 должен быть равен 3 или 5);

· m=2 (1>4).

при соблюдении этих ограничений, длина периода будет равна m/4.

Смешанный конгруэнтный метод генерации последовательности случайных чисел

соотношение смешанного конгруэнтного метода выглядит так: x_n+1=(ax_n+c) mod m, где n > 0. при правильном подборе начальных значений элементов кроме увеличения периода последовательности случайных чисел уменьшается корреляция (зависимость) получаемых случайных чисел.

на значения накладываются ограничения:

· х₀>0;

· а=2¹+1, где 1>=2;

· с>0 взаимно просто с m (это выполнимо, если с — нечетно, а т=2^р, где (р>=2)

· m=2^р (р>=2) и т кратно 4.

43.Укажите, какие функции используются для генерации случайных чисел с различными законами распределения в системе MATLAB

Функция randn генерирует массив со случайными элементами, распределенными по нормальному закону с нулевым математическим ожиданием и среднеквадратическим отклонением, равным 1:

· randn(n) — возвращает матрицу размера nхn. Если n — не скаляр, то появится сообщение об ошибке;

· randn(m.n) или randn([m n]) — возвращают матрицу размера mxn;

· randn(m,n,p,...) или randn([m n р...]) — возвращает массив с элементами, значения которых распределены по нормальному закону;

· randn(size(A)) — возвращает массив того же размера, что и А, с элементами, распределенными по нормальному закону;

· randn (без аргументов) — возвращает одно случайное число, которое изменяется при каждом последующем вызове и имеет нормальное распределение;

· randn( 'state') — возвращает двухэлементный вектор, включающий текущее состояние нормального генератора. Для изменения состояния генератора можно применять следующие формы этой функции:

o randn('state',s) — устанавливает состояние в s;

o randn('state' ,0) — сбрасывает генератор в начальное состояние;

o randn('state', j) — для целых j устанавливает генератор в J-e состояние;

o randn('state', sum( 100*clock)) — каждый раз сбрасывает генератор в состояние, зависящее от времени.

Функция rand генерирует массивы случайных чисел, значения элементов которых равномерно распределены в промежутке (0, 1):

· rand(n) — возвращает матрицу размера nхn. Если n — не скаляр, то появится сообщение об ошибке;

· rand(m.n) или rand([m п]) — возвращают матрицу размера mxn;

· rand(m.n,p....) или rand([m n р...]) — возвращает многомерный массив;

· rand(size(A)) — возвращает массив того же размера и размерности, что и А, с элементами, распределенными по равномерному закону;

· rand (без аргументов) — возвращает одно случайное число, которое изменяется при каждом последующем вызове и имеет равномерный закон распределения;

· rand(' state') — возвращает вектор с 35 элементами, содержащий текущее состояние генератора случайных чисел с равномерным распределением. Для изменения состояния генератора можно применять следующие формы этой функции:

o rand('state' .s) — устанавливает состояние в s;

o rand( 'state' ,0) — сбрасывает генератор в начальное состояние;

o rand( 'state'. j) — для целых j, устанавливает генератор в j-е состояние;

o rand( 'state' ,sum(100*clock)) — каждый раз сбрасывает генератор в состояние, зависящее от времени.

POISSRND - Функция генерации псевдослучайных чисел по закону Пуассона

R = poissrnd(LAMBDA) функция предназначена для генерации псевдослучайного числа по распределению Пуассона для каждого значения параметра LAMBDA. Размерность матрицы R равна размерности входного параметра. R = poissrnd(LAMBDA,m) позволяет получить вектор псевдослучайных чисел на m элементов распределенных по закону Пуассона для параметра LAMBDA, где m - вектор размерностью 1x2 определяющий размерность матрицы R. R = poissrnd(LAMBDA,m,n) позволяет получить матрицу псевдослучайных чисел с размерностью m-n элементов распределенных по закону Пуассона для параметра LAMBDA.

RANDOM- Параметрическая функция генерации псевдослучайных чисел

y = random('name',A1,A2,A3,m,n) возвращает матрицу случайных чисел согласно заданному распределению. Вид распределения задается значением параметра 'name' в соответствии со следующей таблицей

Параметры A1, A2, A3 яв-ся параметрами перечисленных выше распределений. Последовательность и количество передаваемых параметров A1, A2, A3 должны соответствовать числу и последовательности передаваемым параметрам соответствующих функций генерации псевдослучайных чисел. Размерность векторов или матриц X, A1, A2, A3 должна быть одинаковой. Размерность скалярного параметра увеличивается до размерности других входных аргументов.

Параметры m и n задают размерность матрицы генерируемых псевдослучайных чисел y. В случае, если параметры распределения A1, A2, A3 заданы как матрицы, то m и n либо могут отсутствовать, либо должны соответствовать размерности указанных переменных.

RAYLRND - Функция генерации псевдослучайных чисел по закону Релея

R = raylrnd(B) функция предназначена для генерации псевдослучайного числа по закону Релея для каждого значения параметра B. Размерность матрицы R равна размерности входного параметра. R = raylrnd(B,m) позволяет получить вектор псевдослучайных чисел на m элементов распределенных по закону Релея для параметра B, где m - вектор размерностью 1x2 определяющий размерность матрицы R. R = raylrnd(B,m,n) позволяет получить матрицу псевдослучайных чисел с размерностью m-n элементов распределенных по закону Релея для параметра LAMBDA.

TRND - Функция генерации псевдослучайных чисел по распределению Стьюдента

R = trnd(V) функция предназначена для генерации псевдослучайного числа по распределению Стьюдента для каждого значения числа степеней свободы V. Размерность матрицы R равна размерности входного параметра. R = trnd(V,m) позволяет получить вектор псевдослучайных чисел на m элементов распределенных по распределению Стьюдента для параметра V, где m - вектор размерностью 1x2 определяющий размерность матрицы R. R = trnd(V,m,n) позволяет получить матрицу псевдослучайных чисел с размерностью m-n элементов распределенных по закону Пуассона для заданного числа степеней свободы V.

44.Дайте определение и приведите основные соотношения для моделирования разомкнутых систем массового обслуживания с отказами

Пусть система работает с отказами. Необходимо определить абсолютную и относительную пропускную способности системы. Система имеет два состояния: S₀ - канал свободен и S₁ - канал занят. Переход из S₀ в S₁ связан с появлением заявки и немедленным началом ее обслуживания. Переход из S₁ в S₀ осуществляется, как только очередное обслуживание завершится.

Представим данную систему массового обслуживания в виде графа (рис. 4.1), у которого имеются два состояния: S₀ - канал свободен (ожидание); S₁ - канал занят (идет обслуживание заявки).

Рис. 4.1. Граф состояний одноканальной СМО с отказами.

Обозначим вероятности состояний: P₀(t) - вероятность состояния «канал свободен»; P₁(t) - вероятность состояния «канал занят». По размеченному графу состояний (рис. 4.1) составим систему дифференциальных уравнений Колмогорова для вероятностей состояний:

(4.5)

Система линейных дифференциальных уравнений (4.12) имеет решение с учетом нормировочного условия P₀(t) + P₁(t) = 1 . Решение данной системы называется неустановившимся, поскольку оно непосредственно зависит от t и выглядит следующим образом:

, (4.6)

P₁(t) = 1 - P₀(t) = 1 . (4.7)

Нетрудно убедиться, что для одноканальной СМО с отказами вероятность P₀(t) есть не что иное, как относительная пропускная способность системы q.

Действительно, P₀ - вероятность того, что в момент t канал свободен и заявка, пришедшая к моменту t, будет обслужена, а следовательно, для данного момента времени t среднее отношение числа обслуженных заявок к числу поступивших также равно P₀(t), т. е.

q = P₀(t), (4.8)

По истечении большого интервала времени (при t"∞) достигается стационарный (установившийся) режим:

, (4.9)

Зная относительную пропускную способность, легко найти абсолютную. Абсолютная пропускная способность (А) - среднее число заявок, которое может обслужить система массового обслуживания в единицу времени:

. (4.10)

Вероятность отказа в обслуживании заявки будет равна вероятности состояния «канал занят»:

. (4.11)

Данная величина P_отк может быть интерпретирована как средняя доля необслуженных заявок среди поданных.

Пример 2.1. Пусть одноканальная СМО с отказами представляет собой один пост ежедневного обслуживания (ЕО) для мойки автомобилей. Заявка - автомобиль, прибывший в момент, когда пост занят, - получает отказ в обслуживании. Интенсивность потока автомобилей λ= 1,0 (автомобиль в час). Средняя продолжительность обслуживания - 1,8 часа. Поток автомобилей и поток обслуживании являются простейшими.

Требуется определить в установившемся режиме предельные значения: 1)относительной пропускной способности q; 2)абсолютной пропускной способности А; 3)вероятности отказа P_отк ;

Сравните фактическую пропускную способность СМО с номинальной, которая была бы, если бы каждый автомобиль обслуживался точно 1,8 часа и автомобили следовали один за другим без перерыва.

Решение

1. Определим интенсивность потока обслуживания: .

2. Вычислим относительную пропускную способность: .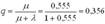

Величина q означает, что в установившемся режиме система будет обслуживать примерно 35% прибывающих на пост ЕО автомобилей.

3. Абсолютную пропускную способность определим по формуле:

Это означает, что система (пост ЕО) способна осуществить в среднем 0,356 обслуживания автомобилей в час.

4. Вероятность отказа: .

Это означает, что около 65% прибывших автомобилей на пост ЕО получат отказ в обслуживании.

5. Определим номинальную пропускную способность системы:

(автомобилей в час).

Оказывается, что А_ном в 1,5 раза больше, чем фактическая пропускная способность, вычисленная с учетом случайного характера потока заявок и времени обслуживания.

45.Дайте определение и приведите основные соотношения для моделирования разомкнутых систем массового обслуживания с очередями

Дата добавления: 2018-05-09; просмотров: 2470; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 345 6 Следующая ⇒

Мы поможем в написании ваших работ!