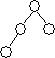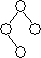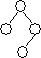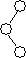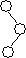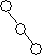ЛЕКЦИЯ 17. БАЛАНСИРОВКА ДЕРЕВА
Цели и задачи лекции..Ознакомиться с алгоритмами балансировки.
Основные рассматриваемые вопросы:построение лозы двоичного дерева, балансировка дерева
Рассмотрим алгоритм баллансировки дерева с помощью лозы.
Алгоритм балансировки состоит из двух частей:
1.дерево преобразуется в лозу.
2.лоза перестраивается в сбалансированное дерево.
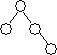
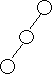
Лоза (vine) — это левоассоциативное двоичное дерево. Она имеет следующий вид:
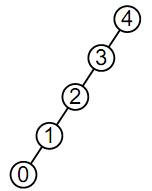
Главная лоза (main vine) — это левоассоциативное поддерево двоичного дерева.
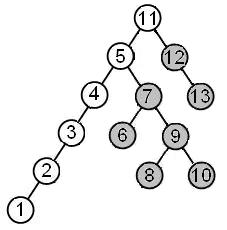
На рисунке вершины главной лозы окрашены в белый цвет.
Преобразование двоичного дерева в лозу.
Мы проходим по дереву указателем p, начиная в корне дерева. Вспомогательный указатель q указывает на родителя p (поскольку мы строим левоассоциативное дерево, то p всегда является левым ребенком q). На каждом шаге возникает одна из двух возможных ситуаций:
· Если у p нет правого ребенка, то эта часть дерева уже перестроена. p и q просто спускаются по дереву (приравниваются своим левым сыновьям).
· Если у p есть правый ребенок (обозначим его r), тогда выполняется левый поворот относительно p:
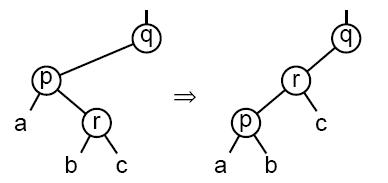
На рисунке a, b и c обозначают поддеревья, которые могут быть пусты. После поворота устанавливаем указатель p на r.
Преобразование лозы в сбалансированное двоичное дерево.
Этот этап алгоритма более содержательный и поэтому менее очевидный. Поэтому сначала будет разобран простой пример, а потом будет дано его обобщение.
Пусть есть лоза, которая состоит из 2n-1 вершин для какого-либо натурального n. Для примера возьмем n=4, тогда лоза будет содержать 15 вершин. Преобразуем данную лозу в сбалансированное дерево за три операции перестроения.
На первой операции пройдем по лозе сверху вниз, начиная в корне, и раскрасим каждую вершину соответственно в серый или черный цвет (условимся, что корень будет серого цвета). Затем возьмем каждую серую вершину, кроме самой нижней, сделаем ее правым ребенком черной вершины, являющейся ее левым ребенком. Т.е. выполним малый правый поворот относительно каждой серой вершины, кроме самой нижней (на рисунке приведен пример малого правого поворота относительно вершины X).
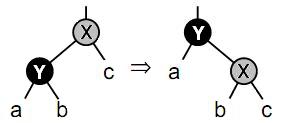
Таким образом, вместо лозы, состоящей из 15 вершин, мы получим дерево, состоящее из 7 черных вершин и 8 серых вершин.
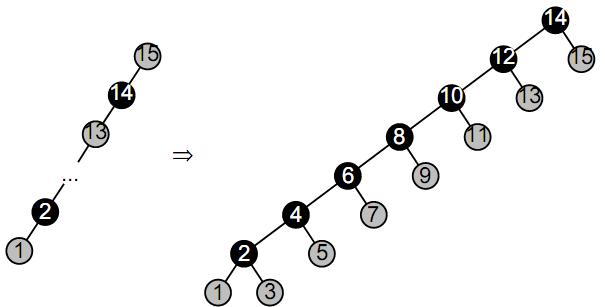
Для второго перестроения сначала перекрасим серые вершины в белые. Далее перекрасим каждую вторую черную вершину в серый цвет, начиная в корне. Теперь, как и раньше, выполним малый правый поворот относительно каждой серой вершины, кроме самой нижней.

Третье перестроение аналогично первым двум. Вершины 12 и 4 перекрашиваются в серый цвет, затем выполняется малый правый поворот относительно вершины 12. В результате получается сбалансированное дерево.
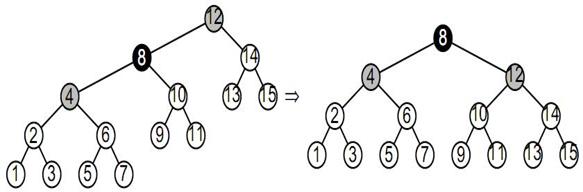
Теперь необходимо разобраться со случаем, когда длина лозы не может быть представлена в виде 2n-1 для какого-либо натурального n. В этом случае необходимо привести длину главной лозы к требуемому значению.
Пусть лоза состоит из m вершин. Тогда существует такое n, что (2n-1) < m < (2n+1-1). Необходимо укоротить главную лозу на m - (2n-1) вершин. После этого можно перестроить получившееся дерево аналогично способу, описанному выше. В результате получится сбалансированное дерево с m - (2n-1) листьями.
Для примера разберем случай, когда лоза состоит из 9 вершин. Отсюда следует, что n=3, т.к. (23-1)=7<9<15=(24-1). Следовательно, необходимо укоротить главную лозу на 9-(23-1)=2. После этого перестраиваем дерево аналогично примеру, приведенному выше. В результате у нас должно получиться сбалансированное дерево.
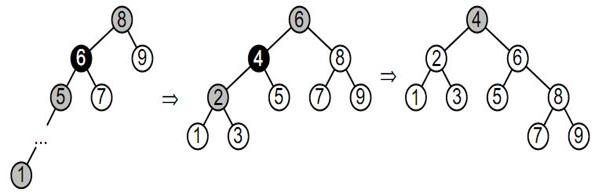
ЛЕКЦИЯ 18. АВЛ-ДЕРЕВЬЯ
Цели и задачи лекции..ознакомиться с АВЛ-деревьями
Основные рассматриваемые вопросы:балансировка АВЛ-дерева.
Критерий идеальной сбалансированности дерева. Дерево называется идеально сбалансированным, если все его уровни, за исключением, может быть, последнего, полностью заполнены. (В бинарном дереве полностью заполненный уровень n содержит 2n узлов).
Если дерево поиска близко к сбалансированному, то даже в худшем случае за время порядка O(logn) в нем можно:
1.Найти вершину с заданным значением или выяснить, что такой вершины нет.
2.Включить новую вершину.
3.Исключить вершину.
Среднее время выполнения этих операций будет также близким к O(log2n), так как в идеально сбалансированном дереве при полностью заполненных уровнях на последнем уровне находится больше половины узлов дерева. Например, последовательность значений 4, 6, 2, 1, 5, 3, 7 дает следующее идеально сбалансированное дерево:
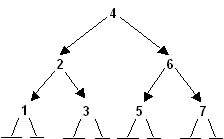
В этом дереве 7 узлов, на последнем уровне находится 4 узла. Если доступ к одному узлу требует 1 единицу времени, то до узла <4> можно добраться за 1 единицу времени, до <2> и <6> - за 2, до <1>, <3>, <5>, <7> - за 3. То есть в худшем случае требуется 3 единицы времени, в среднем: (1+2*2+3*4)/7 = 2.4 единицы времени.
Однако значения в последовательности могут идти и в другом порядке, что может привести к построению несбалансированного дерева. В худшем случае можно получить вырожденное дерево, подобное линейному списку. Например, последовательность значений 1, 7, 2, 6, 3, 5, 4 дает следующее вырожденное дерево:
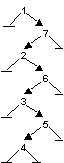
Работа с таким вырожденным деревом потребует в худшем случае 7 единиц времени (доступ к <4>), а в среднем: (1+2+3+4+5+6+7)/7 = 4 единицы времени. То есть для вырожденного дерева затраты на доступ к узлам в худшем случае имеют порядок O(n), в среднем - O(n/2).
Разница во времени доступа будет гораздо заметнее при большем числе узлов. Например, в идеально сбалансированном дереве из 1023 узлов время доступа в худшем случае будет равно 10 единицам времени, в среднем:
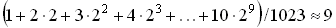 единицам времени.
единицам времени.
А в вырожденном дереве из 1023 узлов потребуется в худшем случае 1023 единицы времени, в среднем - 512 единиц времени.
Поэтому при работе с деревьями поиска больших размеров крайне желательно, чтобы они были близки к сбалансированным.
Приведение уже существующего дерева к идеально сбалансированному - процесс сложный. Проще балансировать дерево в процессе его роста (после включения каждого узла). Однако требование идеальной сбалансированности делает и этот процесс достаточно сложным, способным затрагивать все узлы дерева.
АВЛ-деревья
В 1962 году советские математики Адельсон-Вельский Г.М. и Ландис Е.А. предложили метод балансировки, требующий после включения или исключения узла лишь локальные изменения вдоль пути от корня к данному узлу, то есть времени не более O(log2n). При этом деревьям разрешается отклоняться от идеальной сбалансированности, но в небольшой степени, чтобы среднее время доступа к узлам было лишь немногим больше, чем в идеально сбалансированном дереве. Такие деревья называются АВЛ-деревьями.
Критерий сбалансированности АВЛ-дерева. Дерево называется сбалансированным тогда и только тогда, когда для каждого его узла высоты его левого и правого поддеревьев отличаются не более чем на единицу.
Примеры АВЛ-сбалансированных деревьев:
| Уровень 0 Уровень 1 Уровень 2 Уровень 3 | 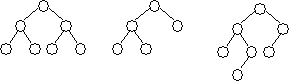
|
Примеры деревьев, не являющихся АВЛ-сбалансированными:
| Уровень 0 Уровень 1 Уровень 2 Уровень 3 | 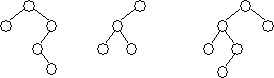
|
Для каждого узла дерева можно определить показатель сбалансированности как разность между высотой правого и левого поддерева данного узла. Пусть hR - высота правого поддерева, - высота левого. Тогда показатель сбалансированности есть hR - hL.
Если дерево АВЛ-сбалансировано, то для каждого узла выполняется: |hR - hL| <= 1. Если хотя бы для одного узла дерева это не так, то дерево не является АВЛ-сбалансированным. Приведем примеры АВЛ-сбалансированного и АВЛ-несбалансированного дерева (у каждого узла указан показатель сбалансированности):
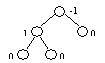 АВЛ-сбалансированное дерево
АВЛ-сбалансированное дерево
| 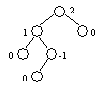 АВЛ-несбалансированное дерево
АВЛ-несбалансированное дерево
|
Включение в АВЛ-дерево
После включения нового узла в АВЛ-дерево оно должно оставаться сбалансированным. Рассмотрим, в каких случаях потребуется балансировка дерева после включения узла. Во всех случаях будем указывать показатель сбалансированности корневого узла
| До включения (дерево АВЛ-сбалансировано) | После включения | |||||||
| В левое поддерево | В правое поддерево | |||||||
 hR = hL hR-hL= 0 hR = hL hR-hL= 0
|
критерий сбалансированности не нарушен |
критерий сбалансированности не нарушен | ||||||
 hR < hL hR-hL= -1 hR < hL hR-hL= -1
|
критерий сбалансированности нарушен, нужна балансировка | 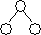 hR = hL hR-hL= 0 критерий сбалансированностине нарушен hR = hL hR-hL= 0 критерий сбалансированностине нарушен
| ||||||
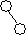 hR > hL hR-hL= 1 hR > hL hR-hL= 1
| 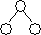 hR = hL hR-hL= 0 критерий сбалансированностине нарушен hR = hL hR-hL= 0 критерий сбалансированностине нарушен
|
критерий сбалансированности нарушен, нужна балансировка | ||||||
Таким образом, есть 4 варианта нарушения балансировки:
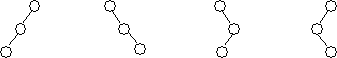
Балансировка выполняется с помощью действий, называемых поворотами узлов. Рассмотрим алгоритмы поворотов, используя указатели p, p1, p2 и считая, что p указывает на узел с нарушенной балансировкой.
Одинарный LL-поворот. Выполняется, когда <перевес> идет по пути L-L от узла с нарушенной балансировкой.
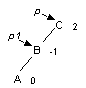
| -> | 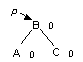
|
p1 := p^.llink;
p^.llink := p1^.rlink;
p1^.rlink := p;
p := p1;
Одинарный RR-поворот.Выполняется, когда <перевес> идет по пути R-R от узла с нарушенной балансировкой.
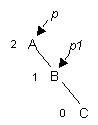
| -> | 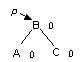
|
p1 := p^.rlink;
p^.rlink := p1^.llink;
p1^.llink := p;
p := p1;
Двойной LR-поворот.Выполняется, когда <перевес> идет по пути L-R от узла с нарушенной балансировкой.
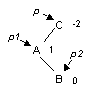
| -> | 
| -> | 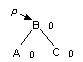
|
p1 := p^.llink;
p2 := p1^.rlink;
p1^.rlink := p2^.llink;
p2^.llink := p1;
p^.llink := p2^.rlink;
p2^.rlink := p;
p := p2;
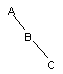
Двойной RL-поворот. Выполняется, когда <перевес> идет по пути R-L от узла с нарушенной балансировкой.
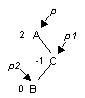
| -> | 
| -> | 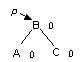
|
p1 := p^.rlink;
p2 := p1^.llink;
p1^.llink := p2^.rlink;
p2^.rlink := p1;
p^.rlink := p2^.llink;
p2^.llink := p;
p := p2;
При включении узлов повороты выполняются для ближайшего узла к включенному с нарушенной балансировкой. То есть если после включения узла в дереве образуется несколько узлов с нарушенной балансировкой, поворот выполняется для того, который находится ниже (то есть ближе к включенному). После балансировки этого узла восстанавливается баланс и выше расположенных узлов.
В качестве примера рассмотрим диаграмму роста АВЛ-дерева поиска, получающегося из последовательности значений 4, 5, 7, 2, 1, 3, 6 (будем указывать тип применяемых поворотов и показатель сбалансированности у узлов с нарушенным балансом):
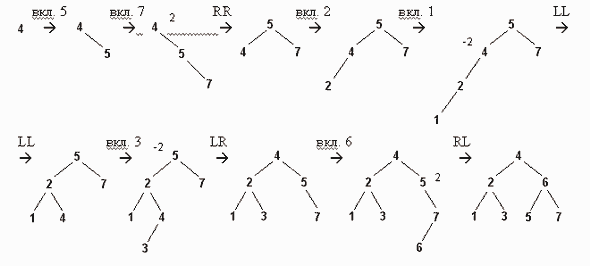
Ясно, что включение узла в АВЛ-дерево в среднем требует больше времени, чем включение в обычное дерево, так как может возникать необходимость проведения балансировки. Поэтому АВЛ-деревья целесообразно использовать в тех случаях, когда поиск узлов в дереве происходит гораздо чаще, чем включение и исключение улов.
Процедура включения в АВЛ-дерево.Для облегчения балансировки при включении узлов будем хранить показатель балансировки в каждом узле:
type ptr = ^node;
node = record
info : integer;
bal : integer;
llink, rlink : ptr;
end;
Исключение из АВЛ-дерева
Исключение узла из АВЛ-дерева производится так же, как и из обычного дерева поиска, но после этого может возникнуть необходимость проведения балансировки. При этом если включение в АВЛ-дерева может потребовать не более одного поворота, то исключение может вызвать несколько поворотов на пути от удаляемого узла до корня дерева.
В качестве примера рассмотрим последовательное исключение узлов 4, 8, 6, 5, 2, 1, 7 из следующего дерева:
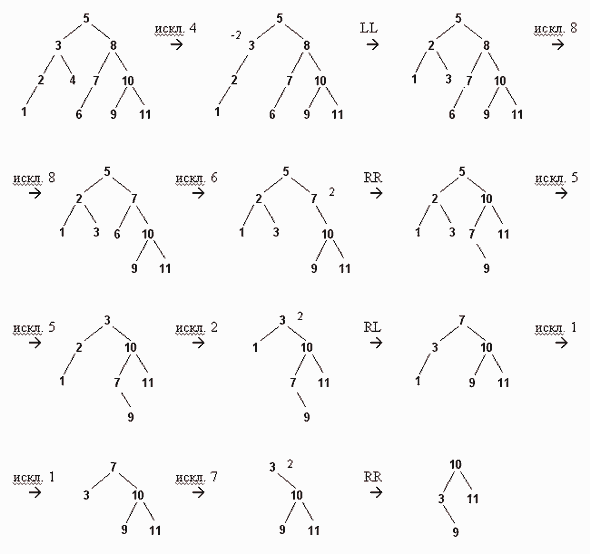
Дата добавления: 2018-05-02; просмотров: 2126; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!