Формула Гаусса–Остроградского
Поверхностные интегралы
 Рассмотрим открытое множество
Рассмотрим открытое множество 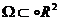 , точки которого будем обозначать
, точки которого будем обозначать  . Пусть
. Пусть 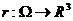 – дифференцируемая функция,
– дифференцируемая функция, 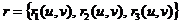 .
.
 Образ отображения
Образ отображения 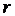 представляет собой при некоторых дополнительных предположениях двухмерную поверхность в
представляет собой при некоторых дополнительных предположениях двухмерную поверхность в  .
.
Рассмотрим векторы
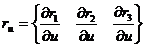 ;
;
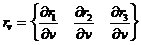 .
.
Они будут касательными к поверхности в текущей точке.
Потребуем, чтобы матрица, состоящая из векторов 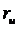 и
и  , имела ранг 2. Тогда
, имела ранг 2. Тогда  – элемент площади поверхности,
– элемент площади поверхности, 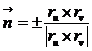 – единичные нормали в текущей точке поверхности.
– единичные нормали в текущей точке поверхности.
Определение.Поверхность ориентируема, если в каждой точке поверхности можно определить нормаль так, чтобы нормали непрерывно изменялись от точки к точке. Такую поверхность также называют двухсторонней.
Формула Гаусса–Остроградского
 Пусть в пространстве дана гладкая двусторонняя поверхность
Пусть в пространстве дана гладкая двусторонняя поверхность  без края, ограничивающая область
без края, ограничивающая область  ,
,
Выберем в каждой точке нормаль 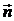 , которая смотрит во внешность относительно
, которая смотрит во внешность относительно  . Таким образом, на
. Таким образом, на 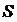 задается ориентация.
задается ориентация.
Пусть задано векторное поле 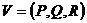 , которое определено в окрестности замыкания
, которое определено в окрестности замыкания 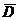 .
.
Определение.Дивергенцией гладкого векторного поля называется следующая функция:
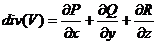 .
.
Теорема (Формула Гаусса–Остроградского). В условиях, приведенных выше, справедлива следующая формула:
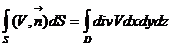 .
.
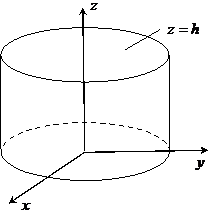 Пример 2.1.14.1. По формуле Гаусса–Остроградского вычислить поверхностный интеграл
Пример 2.1.14.1. По формуле Гаусса–Остроградского вычислить поверхностный интеграл 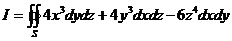 , где
, где  – полная поверхность цилиндра
– полная поверхность цилиндра  ,
, 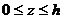 .
.
Решение.
Определяем 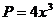 ,
, 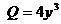 ,
, 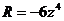 . Затем находим производные
. Затем находим производные  ,
, 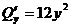 ,
,  . По формуле Гаусса–Остроградского вместо исходного поверхностного интеграла по замкнутой поверхности
. По формуле Гаусса–Остроградского вместо исходного поверхностного интеграла по замкнутой поверхности  получим тройной интеграл по области
получим тройной интеграл по области 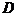 , ограниченной этой поверхностью:
, ограниченной этой поверхностью:
|
|
|
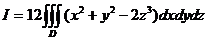 .
.
Переходя к цилиндрическим координатам, найдем
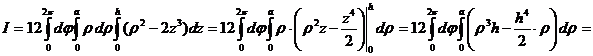
 .
.
Формула Стокса
Определение.Ротор (вихрь) векторного поля  задается следующей формулой:
задается следующей формулой:
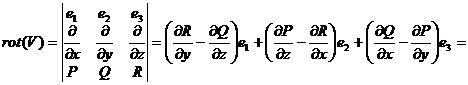
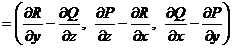 .
.
Формула Стокса
 Пусть дана ориентированная полем единичных нормалей гладкая поверхность
Пусть дана ориентированная полем единичных нормалей гладкая поверхность  в
в  , граница
, граница  состоит из конечного числа гладких кривых.
состоит из конечного числа гладких кривых.
Рассмотрим кривую  (один из кусков границы). Зададим ориентацию
(один из кусков границы). Зададим ориентацию 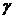 так, чтобы направление обхода было согласовано с вектором нормали. Будем обходить кривую
так, чтобы направление обхода было согласовано с вектором нормали. Будем обходить кривую 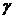 так, что если смотреть на поверхность с конца нормали, то обход границы осуществляется в том же направлении, в каком поворот вектора
так, что если смотреть на поверхность с конца нормали, то обход границы осуществляется в том же направлении, в каком поворот вектора 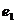 ортонормированного правильного базиса
ортонормированного правильного базиса 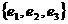
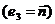 до совмещения с вектором
до совмещения с вектором  меньше. Тогда ориентированная граница называется согласованно ориентированной с ориентацией поверхности. Зададим гладкое векторное поле
меньше. Тогда ориентированная граница называется согласованно ориентированной с ориентацией поверхности. Зададим гладкое векторное поле 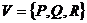 в окрестности поверхности.
в окрестности поверхности.
Теорема (формула Стокса). В условиях, приведенных выше, справедлива формула:
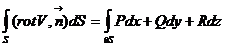 .
.
Пример 2.1.15.1. Применяя формулу Стокса, найти 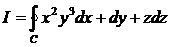 , если
, если 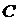 – окружность
– окружность  ,
, 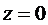 .
.
|
|
|
Решение.
Радиус-вектор для окружности  ,
, 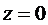 равен
равен 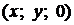 . Тогда
. Тогда
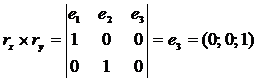 ;
;
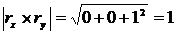 ;
;
 ;
;
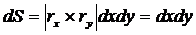 .
.
Учитывая, что 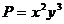 ,
,  ,
,  , получим
, получим

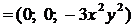 .
.
По формуле Стокса получаем
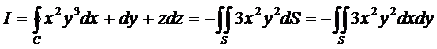 ,
,
где плоская область 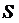 ограничена окружностью
ограничена окружностью 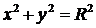 . Вводя полярные координаты
. Вводя полярные координаты  ,
, 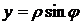 , получим
, получим
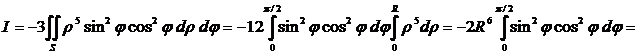
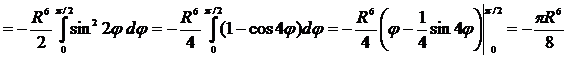 .
.
Дата добавления: 2018-04-15; просмотров: 302; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
