Зависимость скорости тела от времени для различных значений ускорения.

Зависимость перемещения тела от времени.
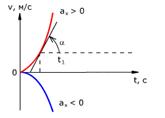
Скорость тела в данный момент времени t1 равна тангенсу угла наклона между касательной к графику и осью времени v = tg α, а перемещение определяют по формуле:
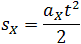
Если время движения тела неизвестно, можно использовать другую формулу перемещения, решая систему из двух уравнений:
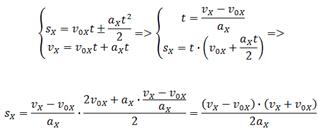
Формула сокращённого умножения разности квадратов поможет нам вывести формулу для проекции перемещения:
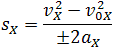
Так как координата тела в любой момент времени определяется суммой начальной координаты и проекции перемещения, то уравнение движения тела будет выглядеть следующим образом:
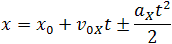
Графиком координаты x(t) также является парабола (как и график перемещения), но вершина параболы в общем случае не совпадает с началом координат. При аx < 0 и х0 = 0 ветви параболы направлены вниз.
Вопрос 5*. Равнопеременное прямолинейное движение ( 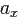 = const). Получите формулы для ΔX через скорость Vx (без t) для равноускоренного движения.
= const). Получите формулы для ΔX через скорость Vx (без t) для равноускоренного движения.
Равнопеременное движение – это движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково.
Ускорение тела при равнопеременном движении остаётся постоянным по модулю и по направлению (a = const).
Равнопеременное движение может быть равноускоренным или равнозамедленным.
Равноускоренное движение – это движение тела (материальной точки) с положительным ускорением, то есть при таком движении тело разгоняется с неизменным ускорением. В случае равноускоренного движения модуль скорости тела с течением времени возрастает, направление ускорения совпадает с направлением скорости движения.
|
|
|
Равнозамедленное движение – это движение тела (материальной точки) с отрицательным ускорением, то есть при таком движении тело равномерно замедляется. При равнозамедленном движении векторы скорости и ускорения противоположны, а модуль скорости с течением времени уменьшается.
В механике любое прямолинейное движение является ускоренным, поэтому замедленное движение отличается от ускоренного лишь знаком проекции вектора ускорения на выбранную ось системы координат.
Если время движения тела неизвестно, можно использовать другую формулу перемещения, решая систему из двух уравнений (вместо Sx подставить ΔX):
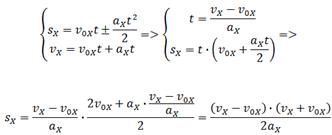
Получаем:
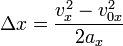
Вопрос.
Движение материальной точки полностью определяется изменением её координат во времени (например, двух на плоскости). Изучением этого занимается кинематика точки. В частности, важными характеристиками движения являются траектория материальной точки, перемещение, скорость и ускорение.
- Прямолинейное движение точки (когда она всегда находится на прямой, скорость параллельна этой прямой)
- Криволинейное движение - это движение точки по траектории, не представляющей собою прямую, с произвольным ускорением и произвольной скоростью в любой момент времени (например, движение по окружности).
Радиус-вектор (обычно обозначается 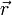 или просто
или просто 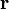 ) — вектор, задающий положения точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.
) — вектор, задающий положения точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.
|
|
|
- Для произвольной точки в пространстве, радиус-вектор — это вектор, идущий из начала координат в эту точку.
- Вектор перемещения - вектор, соединяющий начальную и конечную точки траектории.
Скорость изменения положения со временем, определяется так:

Ускорение, или скорость изменения скорости, это:
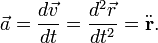
Вопрос.
Движение материальной точки полностью определяется изменением её координат во времени (например, двух на плоскости). Изучением этого занимается кинематика точки. В частности, важными характеристиками движения являются траектория материальной точки, перемещение, скорость и ускорение.
- Прямолинейное движение точки (когда она всегда находится на прямой, скорость параллельна этой прямой)
- Криволинейное движение - это движение точки по траектории, не представляющей собою прямую, с произвольным ускорением и произвольной скоростью в любой момент времени (например, движение по окружности).
|
|
|
при равномерном движении по окружности путь равен длине дуги, то для линейной скорости имеет место равенство:
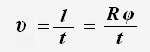
Вопрос.
Движение материальной точки полностью определяется изменением её координат во времени (например, двух на плоскости). Изучением этого занимается кинематика точки. В частности, важными характеристиками движения являются траектория материальной точки, перемещение, скорость и ускорение.
o Прямолинейное движение точки (когда она всегда находится на прямой, скорость параллельна этой прямой)
o Криволинейное движение - это движение точки по траектории, не представляющей собою прямую, с произвольным ускорением и произвольной скоростью в любой момент времени (например, движение по окружности).
Закон движения — математическая формулировка того, как движется тело или как происходит движение более общего вида или набор зависимостей, которые выявляют все данные о движении точки.
В классической механике материальной точки закон движения представляет собой три зависимости трёх пространственных координат от времени, либо зависимость одной векторной величины (радиус-вектора) от времени, вида
|
|
|
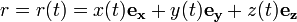
Закон движения может быть найден, в зависимости от задачи, либо из дифференциальных законов механики (см. Законы Ньютона), либо из интегральных (см. Закон сохранения энергии,Закон сохранения импульса), либо из так называемых вариационных принципов.
Вопрос.
Тангенциальное ускорение — компонента ускорения, направленная по касательной к траектории движения. Совпадает с направлением вектора скорости при ускоренном движении и противоположно направлено при замедленном. Характеризует изменение модуля скорости.
Величину тангенциального ускорения - в смысле проекции вектора ускорения на единичный касательный вектор траектории - можно выразить так:

где 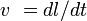 - путевая скорость вдоль траектории, совпадающая с абсолютной величиной мгновенной скорости в данный момент.
- путевая скорость вдоль траектории, совпадающая с абсолютной величиной мгновенной скорости в данный момент.
Если использовать для единичного касательного вектора обозначение  , то можно записать тангенциальное ускорение в векторном виде:
, то можно записать тангенциальное ускорение в векторном виде:
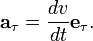
Вопрос
центростремительное ускорение — часть полного ускорения точки, обусловленного кривизной траектории и скоростью движения по ней материальной точки. Такое ускорение направлено к центру кривизны траектории, чем и обусловлен термин. Формально и по существу термин центростремительное ускорение в целом совпадает с термином нормальное ускорение, различаясь скорее лишь стилистически
формула:

или

где 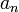 — нормальное (центростремительное) ускорение,
— нормальное (центростремительное) ускорение, 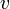 — (мгновенная) линейная скорость движения по траектории,
— (мгновенная) линейная скорость движения по траектории, 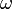 — (мгновенная) угловая скорость этого движения относительно центра кривизны траектории,
— (мгновенная) угловая скорость этого движения относительно центра кривизны траектории,  — радиус кривизны траектории в данной точке. (Связь между первой формулой и второй очевидна, учитывая
— радиус кривизны траектории в данной точке. (Связь между первой формулой и второй очевидна, учитывая  ).
).
Выражения выше включают абсолютные величины. Их легко записать в векторном виде, домножив на 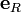 — единичный вектор от центра кривизны траектории к данной ее точки:
— единичный вектор от центра кривизны траектории к данной ее точки:
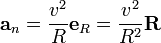
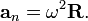
Эти формулы равно применимы к случаю движения с постоянной (по абсолютной величине) скоростью, так и к произвольному случаю. Однако во втором надо иметь в виду, что центростремительное ускорение не есть полный вектор ускорения, а лишь его составляющая, перпендикулярная траектории (или, что то же, перпендикулярная вектору мгновенной скорости); в полный же вектор ускорения тогда входит еще и тангенциальная составляющая (тангенциальное ускорение) 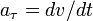 , по направлению совпадающее с касательной к траектории (или, что то же, с мгновенной скоростью)
, по направлению совпадающее с касательной к траектории (или, что то же, с мгновенной скоростью)
11 вопрос.
Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой 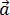 n. Вектор нормального ускорения направлен по радиусу кривизны траектории.
n. Вектор нормального ускорения направлен по радиусу кривизны траектории.
Вектор ускорения

при движении точки по окружности можно разложить на два слагаемых (компоненты):
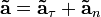
Тангенциальное ускорение — 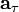 направлено по касательной к траектории (обозначается иногда
направлено по касательной к траектории (обозначается иногда 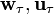 и т.д., в зависимости от того, какой буквой в данной книге принято обозначать ускорение). Является составляющей вектора ускорения a. Характеризует изменение скорости по модулю.
и т.д., в зависимости от того, какой буквой в данной книге принято обозначать ускорение). Является составляющей вектора ускорения a. Характеризует изменение скорости по модулю.

Центростремительное или Нормальное ускорение 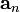 — возникает (не равно нулю) всегда при движении точки по окружности (конечного радиуса) (также обозначается иногда
— возникает (не равно нулю) всегда при движении точки по окружности (конечного радиуса) (также обозначается иногда 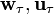 итд). Является составляющей вектора ускорения a, перпендикулярной вектору мгновенной скорости. Вектор нормального ускорения всегда направлен к центру окружности, а модуль равен:
итд). Является составляющей вектора ускорения a, перпендикулярной вектору мгновенной скорости. Вектор нормального ускорения всегда направлен к центру окружности, а модуль равен:

Угловое ускорение — показывает, на сколько изменилась угловая скорость за единицу времени, и, по аналогии с линейным ускорением, равно:

Направление вектора здесь показывает, увеличивается или уменьшается модуль скорости. Если векторы углового ускорения и скорости сонаправлены, значение скорости растёт, и наоборот.
Вопрос.
Движение тела, брошенного горизонтально
Если скорость 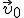 направлена не вертикально, то движение тела будет криволинейным.
направлена не вертикально, то движение тела будет криволинейным.

Рис. 1
Рассмотрим движение тела, брошенного горизонтально с высоты h со скоростью 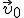 (рис. 1). Сопротивлением воздуха будем пренебрегать. Для описания движения необходимо выбрать две оси координат — Ox и Oy. Начало отсчета координат совместим с начальным положением тела. Из рисунка 1 видно, что υ0x = υ0, υ0y = 0, gx = 0, gy = g.
(рис. 1). Сопротивлением воздуха будем пренебрегать. Для описания движения необходимо выбрать две оси координат — Ox и Oy. Начало отсчета координат совместим с начальным положением тела. Из рисунка 1 видно, что υ0x = υ0, υ0y = 0, gx = 0, gy = g.
Тогда движение тела опишется уравнениями:
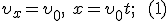

Анализ этих формул показывает, что в горизонтальном направлении скорость тела остается неизменной, т. е. тело движется равномерно. В вертикальном направлении тело движется равноускоренно с ускорением  , т. е. так же, как тело, свободно падающее без начальной скорости. Найдем уравнение траектории. Для этого из уравнения (1) найдем время
, т. е. так же, как тело, свободно падающее без начальной скорости. Найдем уравнение траектории. Для этого из уравнения (1) найдем время 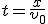 и, подставив его значение в формулу (2), получим:
и, подставив его значение в формулу (2), получим: 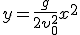 .
.
13 вопрос.
Уравнение траектории тела, брошенного горизонтально
Если построить траекторию движения тела, брошенного горизонтально, в системе координат xy, приняв за начало отсчета координат точку бросания, а направление оси ординат совпадающим с направлением вектора ускорения свободного падения, то координаты каждой точкиP траектории представляют собой перемещение тела в горизонтальном направлении (движение с постоянной скоростью u0) и в вертикальном направлении (равномерно ускоренное движение с ускорением g)

Здесь:
x, y — координаты тела,
u0 — начальная скорость тела (м/с),
g — ускорение свободного падения 9.81 (м/c2),
t — время движения (c)
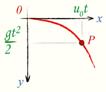
Уравнение траектории тела, брошенного горизонтально
Уравнение траектории тела, брошенного горизонтальновыглядит следующим образом:

Так как ускорение свободного падения g и начальная скорость телаu0 — постоянные величины, то координата y пропорциональна квадрату x, т.е. траектория движения представляет собойпараболу, вершина которой находится в начальной точке движения.
Вопрос.
Зная высоту h, с которой брошено тело, можно найти время t1, через которое тело упадет на землю. В этот момент координата y равна высоте: y1 = h. Из уравнения (2) находим: 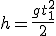 . Отсюда
. Отсюда

Формула (3) определяет время полета тела. За это время тело пройдет в горизонтальном направлении расстояние l, которое называют дальностью полета и которое можно найти на основании формулы (1), учитывая, что l1 = x. Следовательно, 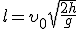 — дальность полета тела. Модуль скорости тела в этот момент
— дальность полета тела. Модуль скорости тела в этот момент 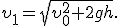 .
.
Вопрос.
Движение тела, брошенного под углом к горизонту.
Пусть тело брошено под углом α к горизонту со скоростью 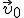 . Как и в предыдущих случаях, будем пренебрегать сопротивлением воздуха. Для описания движения необходимо выбрать две оси координат — Ox и Oy (рис. 1). Начало отсчета совместим с начальным положением тела. Проекции начальной скорости на оси Oy и Ox:
. Как и в предыдущих случаях, будем пренебрегать сопротивлением воздуха. Для описания движения необходимо выбрать две оси координат — Ox и Oy (рис. 1). Начало отсчета совместим с начальным положением тела. Проекции начальной скорости на оси Oy и Ox: 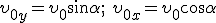 . Проекции ускорения: gx = 0; gy = -g.
. Проекции ускорения: gx = 0; gy = -g.
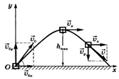
Рис. 1
Тогда движение тела будет описываться уравнениями:
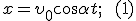

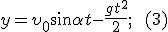
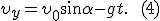
Из этих формул следует, что в горизонтальном направлении тело движется равномерно со скоростью 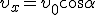 , а в вертикальном — равноускорено.
, а в вертикальном — равноускорено.
21. Кинематика вращательного движения твердого тела с постоянным угловым ускорением: выражения для угловой скорости и угла поворота как функций времени.
Вращательное движение тела или точки характеризуется углом поворота, угловой скоростью и угловым ускорением.
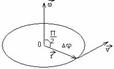
Угол поворота ϕ - это угол между двумя последовательными положениями радиуса вектора r, соединяющего тело или материальную точку с осью вращения. Угловое перемещение измеряется в радианах.
Угловая скорость - векторная физическая величина, показывающая, как изменяется угол поворота в единицу времени и численно равная первой производной от угла поворота по времени, т.е. ω=dϕ/dt. Направление вектора угловой скорости совпадает с направлением вектора углового перемещения, т.е. вектора, численно равного углу ϕ и параллельного оси вращения; оно определяется по правилу буравчика: если совместить ось буравчика с осью вращения и поворачивать его в сторону движения вращающейся точки, то направление поступательного перемещения буравчика определит направление вектора угловой скорости. Точка приложения вектора произвольна, это может быть любая точка плоскости, в которой лежит траектория движения. Удобно совмещать этот вектор с осью вращения.
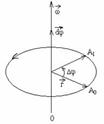
22.Связь между линейным и угловыми характеристиками движения материальной точки вращающегося тела. Тангенциальное, нормальное и полное ускорения точки как функции угловой скорости и углового ускорения.
Отдельные точки вращающегося тела имеют различные линейные скорости v, которые непрерывно изменяют свое направление и зависят от угловой скорости ω и расстояния r соответствующей точки до оси вращения. Точка, находящаяся на расстоянии r от оси вращения проходит путь ΔS = rΔφ. Поделим обе части равенства на Δt :  . Переходя к пределам при
. Переходя к пределам при 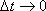 , получим
, получим  , или, согласно
, или, согласно 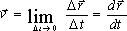 и
и  , получим
, получим 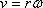 .
.
Таким образом, чем дальше отстоит точка от оси вращения, тем больше ее линейная скорость. По определению ускорения,  , или, с учетом [
, или, с учетом [  ] и [
] и [ 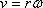 ], получим [
], получим [  ].
].
Для 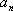 из формулы (
из формулы ( 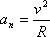 ) с учетом (
) с учетом ( 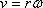 ) можно получить: (
) можно получить: ( 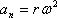 )
)
Из формул видно, что значения линейной скорости, тангенциального и нормального ускорений растут по мере удаления от оси вращения. Формула ( 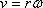 ) устанавливает связь между модулями векторов v, r, ω, которые перпендикулярны друг к другу.
) устанавливает связь между модулями векторов v, r, ω, которые перпендикулярны друг к другу.
23. Вектор угловой скорости. Связь между линейной и угловой скоростью в векторном виде.
Величину  (1)
(1)
называют угловой скоростью. Угловая скорость представляет собой вектор, направление которого связывают с направлением оси вращения тела (рис.1).
Рисунок 1
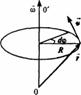
Обратим внимание на то, что, в то время как сам угол поворота φ является скаляром, бесконечно малый поворот dφ — векторная величина, направление которой определяется по правилу правой руки, или буравчика, и связано с осью вращения.
Нетрудно получить связь между угловой и линейной скоростью точки. При движении по окружности элемент дуги связан с бесконечно малым поворотом соотношением dS = R·dφ. Подставив его в (1), находим
v = ωr. (2)
Формула (2) связывает величины угловой и линейной скоростей. Соотношение, связывающее векторы ω и v, следует из рис 1. А именно, вектор линейной скорости представляет собой векторное произведение вектора угловой скорости и радиуса-вектора точки r:
 (3)
(3)
Таким образом, вектор угловой скорости направлен по оси вращения точки и определяется по правилу правой руки или буравчика.
24. Инерциальные системы отсчета и первый закон Ньютона.
Формулировка первого закона Ньютона, экспериментальная основа которого была создана опытами, Галилея еще в 1636 году, неоднократно изменялась, но суть его оставалась одной и той же. В настоящее время используются две формулировки этого закона. Чаще всего употребляется следующая:
Существуют такие системы отсчета, относительно которых поступательно движущееся тело сохраняет свою скорость постоянной, если на него не действуют другие тела или действие других тел скомпенсировано.
Первый закон Ньютона формулируют и по иному.
Тело сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока не подвергнется некомпенсированному воздействию со стороны других тел или физических полей.
Физический смысл: 1) Закон утверждает, что будет происходить с телом, если на него не действуют другие тела или действие других тел скомпенсировано. 2) Из всех систем отсчета первый закон Ньютона выделяет те, где он выполняется; такие системы отсчета называются инерциальными.
Явление сохранения телом, не подверженным некомпенсированным внешним воздействиям, своей скорости постоянной (в том числе равной нулю, если тело покоится) называют инерцией, а системы отсчета, относительно которых такие тела движутся с постоянной скоростью или покоятся, называются инерциальными. В связи с этим первый закон Ньютона часто называют законом инерции. Прямолинейное равномерное движение тела в инерциальной системе отсчета называют движением по инерции. Понятие инерциальной системы отсчёта является фундаментальным в физике вообще и в механике в частности.
Законы механики не зависят от того, к какой инерциальной системе отсчета они относятся. Иными словами, все инерциальные системы отсчета для любых механических явлений равноправны, т.е. не существует какой-либо особой, «главной» инерциальной системы отсчета, движение относительно которой можно было бы рассматривать как «абсолютное движение».
25. 1)Масса, импульс, сила. Второй закон Ньютона (запись через ускорение и через импульс). 2)Формула для изменения импульса точки (через вектор силы). Средняя сила.
1)Второй закон Ньютона в современной формулировке звучит так: в инерциальной системе отсчета скорость изменения импульса материальной точки равна векторной сумме всех сил, действующих на эту точку.
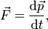
где 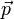 − импульс материальной точки,
− импульс материальной точки,  − суммарная сила, действующая на материальную точку. Второй закон Ньютона гласит, что действие несбалансированных сил приводит к изменению импульса материальной точки.
− суммарная сила, действующая на материальную точку. Второй закон Ньютона гласит, что действие несбалансированных сил приводит к изменению импульса материальной точки.
По определению импульса:

где  − масса,
− масса, 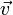 − скорость.
− скорость.
По правилу нахождения производной произведения:
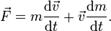
Если масса материальной точки остается неизменной, то производная по времени от массы равна нулю, и уравнение принимает вид:
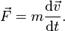
Учитывая определение ускорения точки, второй закон Ньютона принимает вид:
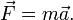
2)Формула для изменения импульса точки через вектор силы:
В новых терминах второй закон Ньютона может быть сформулирован следующим образом: изменение импульса тела (количества движения) равно импульсу силы.
Обозначив импульс тела p буквой второй закон Ньютона можно записать в виде 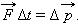
Именно в таком общем виде сформулировал второй закон сам Ньютон. Сила F в этом выражении представляет собой равнодействующую всех сил, приложенных к телу. Это векторное равенство может быть записано в проекциях на координатные оси: Fx Δt = Δpx; Fy Δt = Δpy; Fz Δt = Δpz
Третий закон Ньютона.
Третий закон Ньютона - физический закон, в соответствии с которым:
Силы взаимодействия двух материальных точек в инерциальной системе отсчета:
- равны по модулю;
- противоположны по направлению; и
- действуют вдоль прямой, соединяющей точки.

ВНЕШНИЕ И ВНУТРЕННИЕ СИЛЫ
. В механике внешними силами по отношению к данной системе материальных точек (т. е. такой совокупности материальных точек, в которой движение каждой точки зависит от положений или движений всех остальных точек) называются те силы, к-рые представляют собою действие на эту систему других тел (других систем материальных точек), не включенных нами в состав данной системы. Внутренними силами являются силы взаимодействия между отдельными материальными точками данной системы. Подразделение сил на внешние и внутренние является совершенно условным: при изменении заданного состава системы некоторые силы, ранее бывшие внешними, могут стать внутренними, и обратно. Так, например, при рассмотрении движения системы, состоящей из земли и ее спутника луны, силы взаимодействия между этими телами будут внутренними силами для этой системы, а силы притяжения солнца, остальных планет, их спутников и всех звезд будут внешними силами по отношению к указанной системе. Но если изменить состав системы и рассматривать движение солнца и всех планет как движение одной общей системы, то внешн. силами будут только силы притяжений, оказываемых звездами; все же силы взаимодействия между планетами, их спутниками и солнцем становятся для этой системы силами внутренними. По существу нет различия между внешними и внутренними силами, относительное же различие между ними определяется лишь в зависимости от того, какие тела мы включаем в рассматриваемую систему и какие считаем не входящими в состав системы. Однако указанное относительное различие сил имеет весьма существенное значение при исследовании движения данной системы; по третьему закону Ньютона (о равенстве действия и противодействия), внутренние силы взаимодействия между каждыми двумя материальными точками системы равны по величине и направлены по одной и той же прямой в противоположные стороны; благодаря этому при разрешении различных вопросов о движении системы материальных точек возможно исключить все внутренние силы из уравнений двшкения системы и тем самым сделать возможным самое исследование о движении всей системы. Этот метод исключения внутренних, в большинстве случаев неизвестных, сил связи имеет существенное значение при выводах различных законов механики системы.
Дата добавления: 2018-04-15; просмотров: 656; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

