Задания для самостоятельного решения
1. Изобразить комплексные числа на комплексной плоскости.
1) 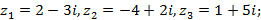
2) 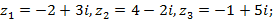
3) 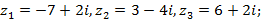
4) 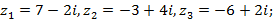
5) 
6) 
7) 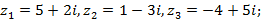
8) 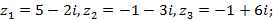
9) 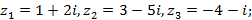
10) 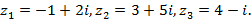
2. Возвести комплексное число  в квадрат.
в квадрат.
1) 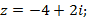 2)
2) 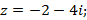 3)
3) 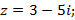
4) 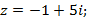 5)
5) 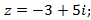 6)
6) 
7) 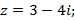 8)
8)  9)
9) 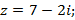
10) 
3. Найти аргумент комплексного числа.
1) 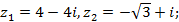
2) 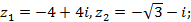
3) 
4) 
5) 
6) 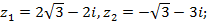
7) 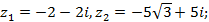
8) 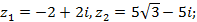
9) 
10) 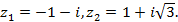
4. Выполнить действия: 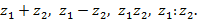
1) 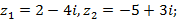
2) 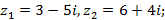
3) 
4) 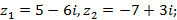
5) 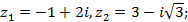
6) 
7) 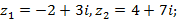
8) 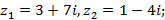
9) 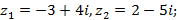
10) 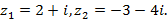
5. Перевести комплексное число в показательную форму и возвести в степень. Ответ записать в алгебраической форме.
1) 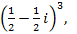 2)
2) 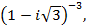 3)
3) 
4) 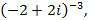 5)
5) 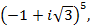 6)
6) 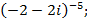
7)  8)
8) 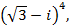 9)
9) 
10) 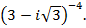
6. Найти модуль комплексного числа.
1) 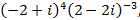
2) 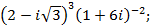
3) 
4) 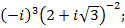
5) 
6) 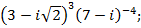
7) 
8) 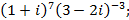
9) 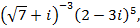
10) 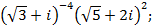
7. Для данного комплексного числа найти модуль и записать комплексно-сопряжённое число.
1) 
2) 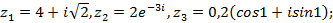
3) 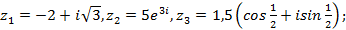
4) 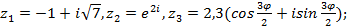
5) 
6) 
7) 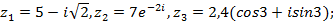
8) 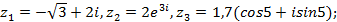
9) 
10) 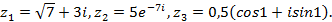
8. Вычислить  если
если  задано, изобразить найденные решения на комплексной плоскости.
задано, изобразить найденные решения на комплексной плоскости.
1) 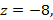 2)
2) 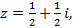 3)
3)  4)
4)  5)
5) 
6) 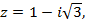 7)
7) 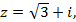 8)
8) 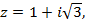 9)
9) 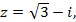
10) 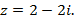
IX. Решить квадратное уравнение.
1) 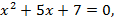 2)
2) 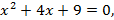 3)
3) 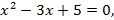
4)  5)
5) 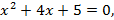 6)
6) 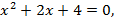
7)  8)
8) 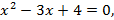 9)
9) 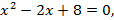
10) 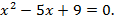
Элементы теории множеств
Понятие множества
Понятие множества относится к числу неопределяемых понятий, таких как, например, понятие точки в геометрии.
Объекты материального мира существуют в составе определенных совокупностей, которые и дают первые примеры множеств: стадо коров, отара овец, множество пальцев на руке и т.п. К примерам множеств, рассматриваемых в математике, относятся: множество всех целых чисел, множество решений данного уравнения, множество всех точек отрезка, множество всех треугольников и т.д.
|
|
|
В результате многократного использования в практической деятельности людей многочисленных примеров совокупностей сформировалось математическое понятие множества, как объединения отдельных объектов в нечто единое целое. Предметы, из которых состоит множество, называются его элементами. Множество считается заданным, если заданы его элементы, оно раз и навсегда определяется своими элементами.
Способы задания множества
Будем обозначать множества большими латинскими буквами: 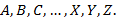 Элементы множеств принято обозначать малыми латинскими буквами
Элементы множеств принято обозначать малыми латинскими буквами 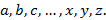 Тот факт, что
Тот факт, что 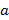 является элементом множества
является элементом множества  , символически записывают
, символически записывают 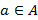 или
или 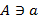 и читают: «
и читают: « 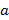 принадлежит
принадлежит  » или «
» или « 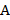 содержит
содержит 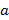 ». Если элемент
». Если элемент 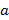 не принадлежит множеству
не принадлежит множеству  , то пишут:
, то пишут: 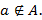
Если множество состоит из конечного числа элементов, то оно называется конечным. В противном случае оно называется бесконечным. Конечное множество в принципе можно задавать перечислением всех его элементов. В этом случае в фигурных скобках записываются все элементы множества или их обозначения. Например 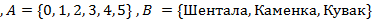 . Однако, если число элементов конечного множества очень велико, то задать его с помощью перечисления всех элементов практически невозможно.
. Однако, если число элементов конечного множества очень велико, то задать его с помощью перечисления всех элементов практически невозможно.
|
|
|
Если множество бесконечно, то задать его перечислением всех элементов нельзя и в теоретическом плане. Такие множества иногда можно задавать в виде 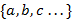 , если по указанным до многоточия элементам можно судить об оставшихся элементах. Например,
, если по указанным до многоточия элементам можно судить об оставшихся элементах. Например, 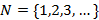 есть множество всех натуральных чисел,
есть множество всех натуральных чисел, 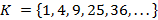 есть множество всех квадратов натуральных чисел.
есть множество всех квадратов натуральных чисел.
Наиболее универсальным способом задания множества является задание его с помощью некоторого характеристического свойства, т.е. такого свойства, которое имеет место для каждого элемента данного множества и которое не выполняется для любого элемента, не принадлежащего данному множеству.
Пусть 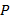 - некоторое свойство. Обозначим через
- некоторое свойство. Обозначим через  утверждение: "Элемент
утверждение: "Элемент  обладает свойством
обладает свойством 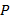 ". Тогда множество всех элементов, обладающих свойством
". Тогда множество всех элементов, обладающих свойством 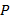 , будем обозначать так:
, будем обозначать так:  . Например,
. Например,  есть множество всех нечетных натуральных чисел. Если множество
есть множество всех нечетных натуральных чисел. Если множество  конструируется из элементов некоторого множества
конструируется из элементов некоторого множества  с помощью характеристического свойства
с помощью характеристического свойства 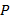 , то можно писать
, то можно писать 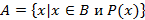 но чаще пишут
но чаще пишут 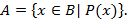
Последняя запись читается так:  есть множество всех элементов из
есть множество всех элементов из  , обладающих свойством
, обладающих свойством 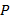 . Например,
. Например, 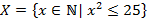 есть множество
есть множество 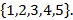 Множество всех натуральных чисел от 10 до 100 можно записать:
Множество всех натуральных чисел от 10 до 100 можно записать: 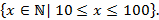 Рассмотрим еще пример. Пусть
Рассмотрим еще пример. Пусть 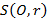 - окружность с центром в точке
- окружность с центром в точке 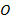 и радиуса
и радиуса  , лежащая в плоскости
, лежащая в плоскости 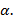 Вспоминая определение окружности, получаем
Вспоминая определение окружности, получаем 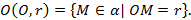
|
|
|
Равенство множеств
Множества  и
и  следует считать равными лишь в том случае, когда они состоят из одних и тех же элементов. Например, если
следует считать равными лишь в том случае, когда они состоят из одних и тех же элементов. Например, если 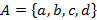 и
и 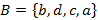 , то
, то  . В частности, порядок расположения элементов в записи множеств при их сравнении во внимание не принимается. Особо следует отметить, что каждый объект может быть элементом множества только один раз, например,
. В частности, порядок расположения элементов в записи множеств при их сравнении во внимание не принимается. Особо следует отметить, что каждый объект может быть элементом множества только один раз, например, 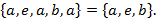
Пустое множество
Не существует ограничения в отношении того, насколько много или мало элементов может быть в одном множестве, множество может состоять из одного элемента, как, например, множество 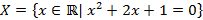 , а может быть и бесконечным, как, например,
, а может быть и бесконечным, как, например, 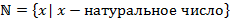 В математике оказывается удобным рассматривать так называемое пустое множество, т.е. такое множество, которое не содержит ни одного элемента. Пустое множество обозначается символом
В математике оказывается удобным рассматривать так называемое пустое множество, т.е. такое множество, которое не содержит ни одного элемента. Пустое множество обозначается символом 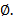 Очевидно, что
Очевидно, что 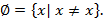 Легко уяснить, что существует лишь одно пустое множество, хотя задано оно может быть различным образом. Так
Легко уяснить, что существует лишь одно пустое множество, хотя задано оно может быть различным образом. Так 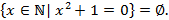
Числовые множества
Математика изучает главным образом такие множества, элементами которых являются математические объекты: точки, линии, формулы, уравнения, функции и т.п. Множества, элементами которых является числа, называются числовыми. Рассмотрим обозначения наиболее употребительных множеств:
|
|
|
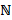 - множество всех натуральных чисел,
- множество всех натуральных чисел,
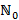 - множество всех целых неотрицательных чисел,
- множество всех целых неотрицательных чисел,
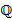 - множество всех рациональных чисел,
- множество всех рациональных чисел,
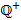 - множество всех рациональных положительных чисел,
- множество всех рациональных положительных чисел,
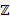 - множество всех целых чисел,
- множество всех целых чисел,
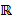 - множество всех вещественных чисел,
- множество всех вещественных чисел,
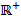 - множество всех положительных вещественных чисел,
- множество всех положительных вещественных чисел,
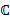 - множество всех комплексных чисел.
- множество всех комплексных чисел.
Приведем еще множества, являющиеся числовыми промежутками.
Пусть 
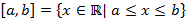 – отрезок,
– отрезок,
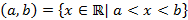 – интервал,
– интервал,
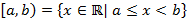 – полуинтервал, замкнутый слева,
– полуинтервал, замкнутый слева,
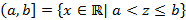 – полуинтервал, замкнутый слева,
– полуинтервал, замкнутый слева,
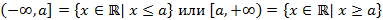 – замкнутый луч,
– замкнутый луч,
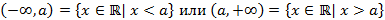 – открытый луч.
– открытый луч.
Подмножество
Множество  называется подмножеством множества
называется подмножеством множества  , есликаждый элемент множества
, есликаждый элемент множества  является элементоми множества
является элементоми множества 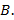 Если
Если  - подмножество
- подмножество  , то пишут
, то пишут  и читают: "
и читают: "  подмножество
подмножество  " или "
" или "  включено в
включено в  ", или "
", или "  включает
включает  ", или"
", или"  содержит
содержит  ". Пустое множество является подмножеством любого множества, так как оно вообще не содержит элементов, а потому и таких элементов, которые не принадлежали бы
". Пустое множество является подмножеством любого множества, так как оно вообще не содержит элементов, а потому и таких элементов, которые не принадлежали бы  . Имеем:
. Имеем: 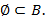
Если  не является подмножеством
не является подмножеством  , то пишут:
, то пишут: 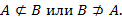
Из определения легко вытекают следующие свойства отношения включения:
1. 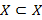 , т.е всякое множество является подмножеством самого себя;
, т.е всякое множество является подмножеством самого себя;
2.  тогда и только тогда, когда
тогда и только тогда, когда 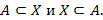
3. Если 
Говорят, что  является собственным подмножеством множества
является собственным подмножеством множества  , если
, если  Например, числовые промежутки являются собственными подмножествами множества вещественных чисел
Например, числовые промежутки являются собственными подмножествами множества вещественных чисел 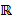 . Множество простых чисел является собственным подмножеством множества натуральных чисел
. Множество простых чисел является собственным подмножеством множества натуральных чисел 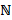 .
.
Пусть  . Множество
. Множество  является подмножеством
является подмножеством  , т.е.
, т.е. 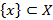 Заметим, что следует различать элемент
Заметим, что следует различать элемент  и одноэлементное множество
и одноэлементное множество  . Так, если
. Так, если 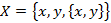 , то
, то 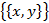 – подмножество
– подмножество  , содержащее один элемент
, содержащее один элемент 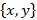 , а {x, y} – подмножество
, а {x, y} – подмножество  , содержащее два элемента
, содержащее два элемента  и
и  . Ясно, что
. Ясно, что 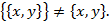
Булеан
Элементы множества сами могут быть некоторыми множествами. Например, элементами множества студенческих групп являются студенческие группы, которые, в свою очередь, являются множествами студентов. Большое применение в математике находит множество, элементами которого являются подмножествами какого-либо множества. Пусть  - некоторое множество. Множество всех подмножеств множества
- некоторое множество. Множество всех подмножеств множества  называетсябулеаном
называетсябулеаном  (в честь ирландского математика и логика Дж.Буля (1815-1864)). Булеан обозначается символом
(в честь ирландского математика и логика Дж.Буля (1815-1864)). Булеан обозначается символом 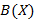 . Итак,
. Итак, 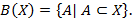 Заметим, что подмножество
Заметим, что подмножество 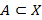 является элементом
является элементом 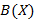 . В частности,
. В частности, 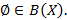
Можно доказать, что если множество  состоит из
состоит из  элементов, то оно содержит
элементов, то оно содержит  подмножеств. Обозначив через
подмножеств. Обозначив через  число элементов конечного множества
число элементов конечного множества  , можно записать
, можно записать 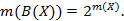
Универсальное множество
Предположим, что изучается некоторая область знаний. Множество, состоящее из всех элементов исследуемой области, называется универсальным. Например, универсальным числовым множеством, рассматриваемым в математике начальной школы, является множество рациональных чисел. Универсальным числовым множеством нашего математического курса является множество вещественных чисел. Заметим, что универсальное множество зависит от того вопроса, который рассматривается, например, при выборе актива группы универсальным множеством является множество студентов группы. Мы будем обозначать универсальное множество символом  . На диаграммах универсальное множество обычно изображается множеством точек некоторого прямоугольника плоскости, а принадлежащие ему подмножества - кругами или овалами внутри прямоугольника.
. На диаграммах универсальное множество обычно изображается множеством точек некоторого прямоугольника плоскости, а принадлежащие ему подмножества - кругами или овалами внутри прямоугольника.
Операции над множествами
Операции над множествами позволяют из имеющихся множеств конструировать новые множества. Рассмотренное выше построение булеана 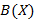 по множеству
по множеству  является примером такого конструирования. Рассмотрим теперь операции над множествами, в известной степени аналогичные алгебраическим операциям над числами.
является примером такого конструирования. Рассмотрим теперь операции над множествами, в известной степени аналогичные алгебраическим операциям над числами.
Объединение множеств.
Объединением данных множеств называется множество, состоящее из тех и только тех элементов, которые принадлежат хотя бы одному из данных множеств.
Если взяты два множества, например  и
и  , то их объединение обозначается символом
, то их объединение обозначается символом 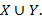 Здесь
Здесь 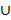 - символ объединения. Итак,
- символ объединения. Итак, 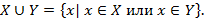
Здесь союз "или" употреблен в неразделительном смысле,т.е. элементы, содержащиеся одновременно в  и
и  , входят в их объединение. Согласно общему принципу образования множества, эти элементы входят в
, входят в их объединение. Согласно общему принципу образования множества, эти элементы входят в 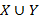 только один раз. Например, если
только один раз. Например, если 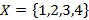 ,
,  , то
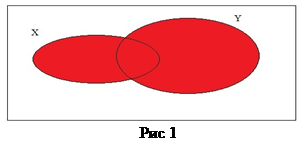
, то 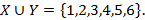 На рис. 1 показана диаграмма, иллюстрирующая объединение двух множеств.
На рис. 1 показана диаграмма, иллюстрирующая объединение двух множеств.
Приведем некоторые свойства операции 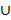 Ниже
Ниже 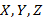 - произвольные множества.
- произвольные множества.
1. Идемпотентность объединения: 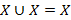 .
.
2. Коммутативность объединения: 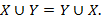
3. Ассоциативность объединения: 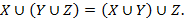
4. 
В силу свойства ассоциативности порядок объединения множеств 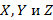 несущественен, поэтому объединение этих множеств записывается в виде:
несущественен, поэтому объединение этих множеств записывается в виде:  . Порядок расположения множеств в объединении тоже несущественен (в силу свойства коммутативности). Поэтому
. Порядок расположения множеств в объединении тоже несущественен (в силу свойства коммутативности). Поэтому  и т. д.
и т. д.
Объединение множеств используется при решении многих математических задач.
Пример.Рассмотрим совокупность уравнений: 
Пусть 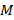 - множество всех решений этой совокупности,
- множество всех решений этой совокупности, 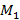 - множество решений уравнения
- множество решений уравнения  , а
, а 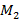 - множество решений уравнения
- множество решений уравнения 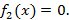 Тогда
Тогда  . Заметим, что к совокупности уравнений может сводится одно уравнение.
. Заметим, что к совокупности уравнений может сводится одно уравнение.
Пересечение множеств
 |
Пересечением данных множеств называется множество всех элементов, принадлежащих каждому из данных множеств. В случае, если даны два множества
 и
и  , то их пересечение обозначается
, то их пересечение обозначается 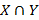 , где
, где 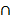 - символ, обозначающий операцию пересечения. Итак,
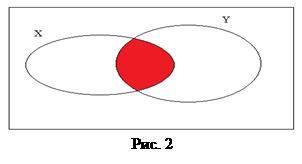
- символ, обозначающий операцию пересечения. Итак, 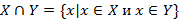 . Пересечение двух множеств на диаграмме изображается общей частью кругов, изображающих пересекаемые множества (рис. 2).
. Пересечение двух множеств на диаграмме изображается общей частью кругов, изображающих пересекаемые множества (рис. 2).
Если 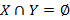 , то говорят, что множества
, то говорят, что множества  и
и  не пересекаются или дизъюнктные.
не пересекаются или дизъюнктные.
Пример 1. Пусть  - множество всех ромбов,
- множество всех ромбов,  - множество всех прямоугольников. Тогда
- множество всех прямоугольников. Тогда 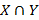 - множество всех квадратов
- множество всех квадратов
Пример 2. Обозначим через 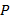 - множество всех простых чисел, пусть
- множество всех простых чисел, пусть  Тогда
Тогда 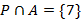 .
.
Приведем основные свойства операции пересечений. Пусть  ,
,  , - произвольные множества.
, - произвольные множества.
1.Пересечение включено в каждоеиз пересекаемых множеств:

2.  , тогда и только тогда, когда
, тогда и только тогда, когда 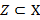 и
и 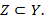
3. Идемпотентность: 
4. Коммутативность: 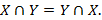
5. Ассоциативность: 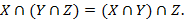
Операция пересечения связана с объединением законами дистрибутивности:
6. 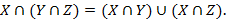
7. 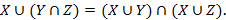
Пересечение множеств используется при решении многих математических задач.
Пример 3.Рассмотрим систему уравнений: 
Пусть 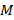 – множество решений этой системы,
– множество решений этой системы, 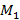 – множество решений уравнения
– множество решений уравнения 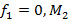 – множество решений уравнения
– множество решений уравнения 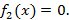 Тогда
Тогда 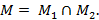
Разность и дополнение
Пример. Тренер по плаванию был предупрежден, что студенты 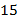 группы не смогут прийти на тренировку, так как на это время им назначена контрольная работа по математике. Его интересует, кто же из студентов, занимающихся плаванием, может быть на тренировке. Взяв список группы по плаванию, тренер вычеркивает из него студентов
группы не смогут прийти на тренировку, так как на это время им назначена контрольная работа по математике. Его интересует, кто же из студентов, занимающихся плаванием, может быть на тренировке. Взяв список группы по плаванию, тренер вычеркивает из него студентов 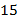 группы. В результате он получает нужный ему список. Операция, проделанная тренером, в теории множеств называется вычитанием. Вычитание обозначается символом
группы. В результате он получает нужный ему список. Операция, проделанная тренером, в теории множеств называется вычитанием. Вычитание обозначается символом  Пусть
Пусть  - множество студентов, занимающихся плаванием,
- множество студентов, занимающихся плаванием,  - множество студентов
- множество студентов 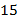 группы. Тогда
группы. Тогда  – множество студентов, которые могут прийти на тренировку.
– множество студентов, которые могут прийти на тренировку.
Разностью множеств  и
и  называется множество всех элементов из
называется множество всех элементов из  , не принадлежащих
, не принадлежащих  . Разность обозначается
. Разность обозначается  (читается: "
(читается: "  минус
минус  "). Согласно определения
"). Согласно определения 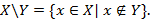
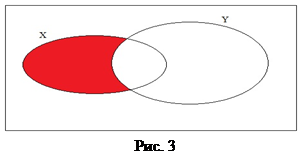 |
На рис.3 показано изображение разности с помощью кругов Эйлера, причем множество
 заштриховано.
заштриховано.
Приведем некоторые свойства операции вычитания.
1. 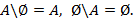
2. 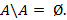
3. 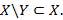
4. 
5. 
 |
Проиллюстрируем на кругах Эйлера свойство 5.
 |
Если
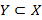 , го разность
, го разность  называют дополнением множества
называют дополнением множества  до множества
до множества  . Дополнение принято обозначать
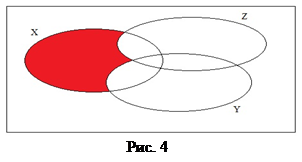
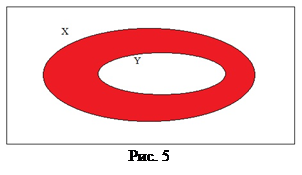
. Дополнение принято обозначать 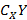 . Графическое изображение дополнения приведено на рис. 5.
. Графическое изображение дополнения приведено на рис. 5.
Если из контекста ясно, до какого множества проводится дополнение, то используется обозначение 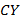 или
или 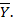 Эти обозначения будут использоваться в дальнейшем. Если при этом в тексте не будет содержаться прямых указаний на множество, до которого производится дополнение, то это будет означать, что оно производится до универсального множества.
Эти обозначения будут использоваться в дальнейшем. Если при этом в тексте не будет содержаться прямых указаний на множество, до которого производится дополнение, то это будет означать, что оно производится до универсального множества.
Рассмотрим важнейшие свойства дополнения.
1. Инволютивность дополнения: 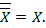
2. Если  , то
, то 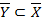 .
.
3. Если  , то
, то 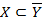 и
и 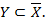
4. Законы де Моргана: 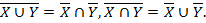
Дата добавления: 2018-04-15; просмотров: 328; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
