Дифференциальные уравнения с разделяющимися переменными
1. Дифференциальное уравнение вида

называется уравнением с разделёнными переменными. После интегрирования уравнения 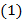 его общее решение получается в неявном виде:
его общее решение получается в неявном виде:
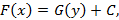
где 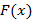 и
и 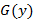 – первообразные соответственно для функций
– первообразные соответственно для функций 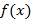 и
и 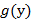 ,
,  -произвольная постоянная.
-произвольная постоянная.
2. Дифференциальное уравнение вида

называется уравнением с разделяющимися переменными. Делим на 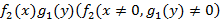 уравнение
уравнение 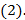 Получаем
Получаем

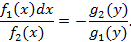
Интегрируем обе части равенства
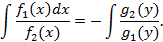
Однородные дифференциальные уравнения
Дифференциальное уравнение первого порядка вида

называется однородным уравнением. Оно приводится к уравнению с разделяющимися переменными с помощью подстановки

Откуда

где 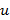 – новая неизвестная функция от
– новая неизвестная функция от  ,
, 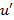 - ее производная по
- ее производная по  .
.
Подставляем 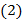 и
и  в
в 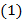
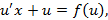
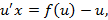
т. к.
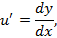
то


Делим на 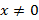
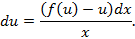
Делим на 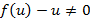
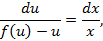

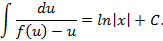
Линейные дифференциальные уравнения. Уравнение
Бернулли
1. Линейным дифференциальным уравнением первого порядка называется уравнение, содержащее неизвестную функцию и ее производную в первой степени:

2. Уравнением Бернулли называется уравнение вида

(при 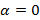 это уравнение является линейным, при
это уравнение является линейным, при 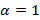 - уравнением с разделяющимися переменными). В
- уравнением с разделяющимися переменными). В 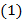 и (2)
и (2) 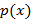 и
и  - заданные функции.
- заданные функции.
Оба типа уравнений можно решать методом Бернулли с помощью подстановки

где 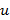 и
и  – новые неизвестные функции от
– новые неизвестные функции от  ,
, 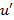 и
и 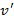 - их производные по x.
- их производные по x.
Рассмотрим решение линейного уравнения.
Подстановка выражений для  и
и 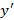 в уравнение
в уравнение 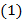 приводит его к виду
приводит его к виду
|
|
|

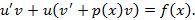
В качестве  выбираем одну из функций, удовлетворяющих уравнению
выбираем одну из функций, удовлетворяющих уравнению

тогда функция 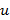 определяется из уравнения
определяется из уравнения

Уравнения 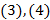 – уравнения с разделяющимися переменными.
– уравнения с разделяющимися переменными.
Рассмотрим решение уравнения 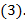

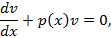

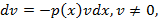
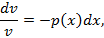
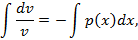
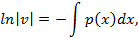

Подставим 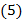 в
в  , найдем функцию
, найдем функцию 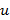 .
.
Дифференциальные уравнения второго порядка
Мы перейдем теперь к изучению дифференциальных уравнений вида
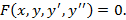
Обычно рассматривают уравнения, разрешенные относительно производной

Начнем с уравнения 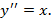
Последовательно интегрируя, найдем сначала первую производную: 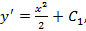 а затем и саму функцию:
а затем и саму функцию:
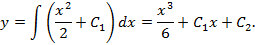
Так как мы интегрировали дважды, то и получили две произвольные постоянные, которые обозначили 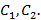
Дифференциальное уравнение второго порядка 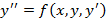 имеет бесчисленное множество решений, которые задаются формулой
имеет бесчисленное множество решений, которые задаются формулой 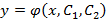 , содержащей две произвольные постоянные. Эта совокупность решений называется общим решением.
, содержащей две произвольные постоянные. Эта совокупность решений называется общим решением.
Частное решение уравнения отыскивается при помощи задания начальных условий

Геометрический смысл начальных условий заключается в том, что помимо точки 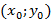 через которую должна проходить интегральная кривая, мы задаем еще угловой коэффициент касательной
через которую должна проходить интегральная кривая, мы задаем еще угловой коэффициент касательной 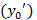 к этой кривой. Отметим, что так как общее решение уравнения второго порядка зависит от двух произвольных постоянных, то через данную точку проходит бесчисленное множество интегральных кривых, лишь одна из которых имеет данный угловой коэффициент.
к этой кривой. Отметим, что так как общее решение уравнения второго порядка зависит от двух произвольных постоянных, то через данную точку проходит бесчисленное множество интегральных кривых, лишь одна из которых имеет данный угловой коэффициент.
Дата добавления: 2018-04-15; просмотров: 339; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
