Операции над матрицами. Обратная матрица. Ранг матрицы
Над матрицами можно производить следующие операции: умножение на число, сложение, умножение матриц и нахождение обратной матрицы. Первые две операции называются линейными.
Произведением матрицы  размера
размера  на число
на число  , называется матрица
, называется матрица 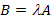 размера
размера  , каждый элемент
, каждый элемент 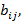 которой равен
которой равен 
Свойства умножения матрицы на число:
1). ассоциативность относительно числового множителя

2) дистрибутивность относительно суммы чисел
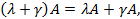
3) дистрибутивность относительно суммы матриц
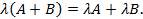
Пример1. 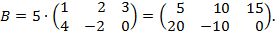

Суммой матриц  и
и  одинакового размера называется матрица
одинакового размера называется матрица 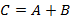 того же размера, каждый элемент
того же размера, каждый элемент 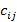 которой равен
которой равен 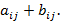
Пример2. 
Матрицы разного размера складывать нельзя.
Эти операции обладают свойствами:
1) коммутативность
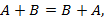
2) ассоциативность
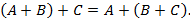
Операцию умножения матриц определим в два этапа.
Из операции умножения матрицы на число можно определить разность матриц как

Произведением строки  из
из  элементов на столбец
элементов на столбец  из
из  элементов называется число
элементов называется число 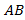 , равное сумме произведений соответствующих элементов строки и столбца, т.е.
, равное сумме произведений соответствующих элементов строки и столбца, т.е.

Строку и столбец разной длины перемножать нельзя.
Пример3. 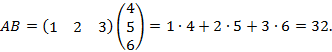
Произведением матрицы  размера
размера  на матрицу
на матрицу  размера
размера 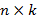 называется матрица
называется матрица  размера
размера 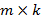 , каждый элемент
, каждый элемент 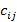 которой равен произведению
которой равен произведению  строки матрицы
строки матрицы  на
на 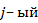 столбец матрицы
столбец матрицы  , т.е.
, т.е.

Пример4. Пусть 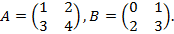 Найдём матрицы
Найдём матрицы 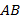 и
и  .
.

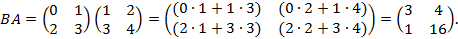
Мы видим, что 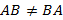 , т.е. умножение матриц свойством коммутативности не обладает.
, т.е. умножение матриц свойством коммутативности не обладает.
|
|
|
Единичная матрица 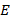 играет роль единицы при умножении на квадратную матрицу, т.е. для любой квадратной матрицы
играет роль единицы при умножении на квадратную матрицу, т.е. для любой квадратной матрицы  верно равенство
верно равенство
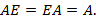
Произведение матриц соответствующих размеров обладает свойствами:
1) ассоциативность

2) ) ассоциативность относительно числового множителя
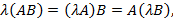
3) дистрибутивностьотносительно суммы матриц

4) антикоммутативность
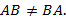
Кроме того, для квадратных матриц 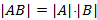 , т.е. определитель произведения матриц равен произведению их определителей.
, т.е. определитель произведения матриц равен произведению их определителей.
Обратной матрицей для квадратной матрицы  называется такая матрица
называется такая матрица 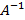 , что выполняется равенство
, что выполняется равенство 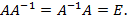
Квадратная матрица  , определитель которой равен нулю, называется вырожденной, матрица, определитель которой не равен нулю, называется невырожденной.
, определитель которой равен нулю, называется вырожденной, матрица, определитель которой не равен нулю, называется невырожденной.
Пример5. Матрица 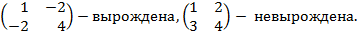
Из соотношения 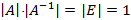 следует, что у вырожденной матрицы не может быть обратной
следует, что у вырожденной матрицы не может быть обратной 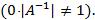
Присоединённой матрицей для квадратной матрицы  называется матрица
называется матрица 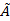 , элементами которой являются алгебраические дополнения соответствующих элементов матрицы
, элементами которой являются алгебраические дополнения соответствующих элементов матрицы  , т.е.
, т.е.

Пример6. Пусть 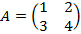 , тогда
, тогда
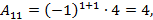
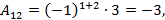

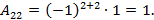

Теорема об обратной матрице. Невырожденные матрицы и только они имеют обратные матрицы, которые находятся по формуле
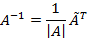
(Здесь 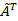 – присоединённая транспонированная матрица).
– присоединённая транспонированная матрица).
|
|
|
Пример7.Найдём обратную матрицу для матрицы 
Поскольку  то обратная матрица существует. В предыдущем примере мы получили, что
то обратная матрица существует. В предыдущем примере мы получили, что  поэтому
поэтому
 и
и
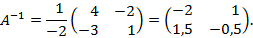
Сделаем проверку.

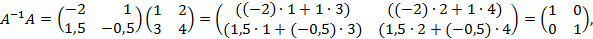
т.е. 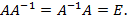
Обратная матрица обладает следующими свойствами:
Если  и
и  невырожденные матрицы, то
невырожденные матрицы, то
1) 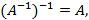
2) 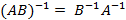 ,
,
3) 
Ранг матрицы
Рассмотрим одну числовую характеристику любой (необязательно квадратной) матрицы. Ранг матрицы определяет число так называемых базисных строк или столбцов матрицы, через которые с помощью линейных операций можно получить все остальные строки или столбцы матрицы.
Минором 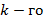 порядка матрицы
порядка матрицы  называется определитель, составленный из элементов стоящих на пересечении произвольно выбранных
называется определитель, составленный из элементов стоящих на пересечении произвольно выбранных 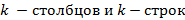 этой матрицы.
этой матрицы.
Рангом матрицы  называется наибольший из порядков ее миноров, не равных нулю.
называется наибольший из порядков ее миноров, не равных нулю.
Он обозначается символом 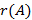 или
или 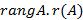 – целое неотрицательное число, не превосходящее числа строк и столбцов матрицы
– целое неотрицательное число, не превосходящее числа строк и столбцов матрицы  . Ранг нулевой матрицы считается равным нулю.
. Ранг нулевой матрицы считается равным нулю.
Для нахождения 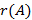 формально необходимо рассмотреть все миноры
формально необходимо рассмотреть все миноры  , начиная с
, начиная с 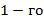 порядка и проверить их на вырожденность.
порядка и проверить их на вырожденность.
Метод окаймляющих миноров позволяет сократить эту процедуру. Он состоит в следующем. Выбираем любой невырожденный минор 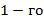 порядка (ненулевой элемент матрицы
порядка (ненулевой элемент матрицы  ). Обозначим его через
). Обозначим его через 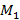 . Затем рассматриваем все миноры 2-го порядка, содержащие M1 (окаймляющие его). Если все они вырождены, то
. Затем рассматриваем все миноры 2-го порядка, содержащие M1 (окаймляющие его). Если все они вырождены, то 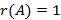 , если нет, то невырожденный минор
, если нет, то невырожденный минор 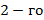 порядка обозначаем через
порядка обозначаем через 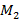 и так далее. Если у матрицы
и так далее. Если у матрицы  есть невырожденный минор
есть невырожденный минор 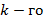 порядка и все окаймляющие его миноры (если они есть) вырождены, то
порядка и все окаймляющие его миноры (если они есть) вырождены, то 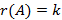 , иначе выбираем минор
, иначе выбираем минор 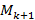 и продолжаем этот процесс.
и продолжаем этот процесс.
|
|
|
Пример9.Найдём ранг матрицы
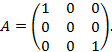
У матрицы выбираем невырожденный минор 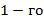 порядка
порядка 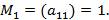 Среди окаймляющих его миноров есть один невырожденный
Среди окаймляющих его миноров есть один невырожденный

Единственный минор 3-го порядка окаймляющий 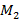 – это сама матрица
– это сама матрица  . Но, поскольку
. Но, поскольку
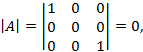
то  – вырождена и
– вырождена и 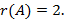
Рассмотрим ещё один метод нахождения 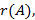 который называется методом элементарных преобразований или методом Гаусса.
который называется методом элементарных преобразований или методом Гаусса.
Элементарными преобразованиями для матрицы A называются следующие её преобразования:
1)Перестановка строк или столбцов местами.
2) Умножение строки или столбца на ненулевой коэффициент.
3) Прибавление к одной строке или столбцу матрицы другой её строки или столбца, умноженной на некоторое число 
4) Зачёркивание нулевой строки или столбца матрицы.
Матрица  , полученная из
, полученная из  с помощью элементарных преобразований, называется эквивалентной ей и обозначается в виде
с помощью элементарных преобразований, называется эквивалентной ей и обозначается в виде 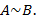
|
|
|
Теорема.При элементарных преобразованиях ранг матрицы не меняется.
Теорема.Ранг треугольной матрицы равен количеству ее ненулевых строк.
Метод Гаусса состоит в том, что с помощью элементарных преобразований матрица  приводится к треугольному виду с ненулевыми элементами на главной диагонали (если матрица не квадратная, то она приводится к ступенчатому виду). Число этих ненулевых элементов совпадает с рангом матрицы.
приводится к треугольному виду с ненулевыми элементами на главной диагонали (если матрица не квадратная, то она приводится к ступенчатому виду). Число этих ненулевых элементов совпадает с рангом матрицы.
Перестановку строк или столбцов местами будем обозначать символом, где стрелки указывают на переставляемые строки или столбцы, а третье элементарное преобразование символом, где стрелка начинается у строки, которую умножаем на l и заканчивается у изменяемой строки.
Пример10. Найдём ранг матрицы

Проведём элементарные преобразования согласно методу Гаусса:
1) поменяем местами первый и второй столбец матрицы;
2) умножим первую строку матрицы поочередно на 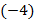 и
и 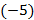 и сложим соответственно со второй и третьей строками;
и сложим соответственно со второй и третьей строками;
3) умножим на (-3) вторую строку и прибавим к третьей;
4) вычеркнем третью нулевую строку.

Следовательно, 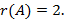
Базисным минором называется любой из отличных от нуля миноров матрицы 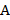 , порядок которого равен
, порядок которого равен 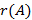 .
.
Примеры.
1. Для данных матриц
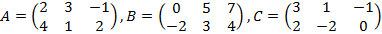
Вычислить 
Решение.
Прежде чем производить линейные действия над матрицами, необходимо убедится в том, что их размерности совпадают. Все три матрицы имеют размерности  по количеству строк и столбцов соответственно. Действия выполняем согласно правилам сложения матриц и умножения матрицы на число:
по количеству строк и столбцов соответственно. Действия выполняем согласно правилам сложения матриц и умножения матрицы на число:

2. Для данных матриц

1) проставить размерность;
2) протранспонировать матрицы;
3) перемножить, если это возможно.
Решение.
а) Размерность матрицы определяется количеством её строк и столбцов. Матрица  имеет две строки и два столбца, матрица
имеет две строки и два столбца, матрица  - две строки и один столбец, и т.д. Поэтому:
- две строки и один столбец, и т.д. Поэтому:
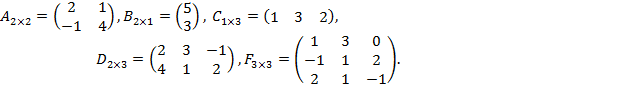
б) Протранспонируем заданные матрицы. Для этого соответствующие строки матриц запишем столбцами:
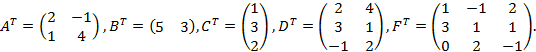
в) Рассмотрим операцию перемножения. Перемножить можно лишь те матрицы, в которых количество столбцов первой матрицы совпадает с количеством строк второй матрицы.
Матрица 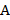 имеет размерность
имеет размерность 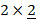 , а матрица
, а матрица  –размерность
–размерность  , поэтому матрицы перемножить можно и в результате перемножения мы получаем матрицу-столбец размерности
, поэтому матрицы перемножить можно и в результате перемножения мы получаем матрицу-столбец размерности  соответствующей крайним индексам матриц
соответствующей крайним индексам матриц 
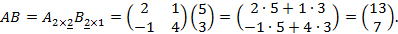
В обратном порядке эти матрицы перемножать нельзя. Произведение
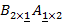
не определено, т.к. внутренние индексы (они подчеркнуты) различны.
Перемножим теперь матрицы  Внутренние индексы совпадают, следовательно, произведение данных матриц определено и в результате получится матрица размерности
Внутренние индексы совпадают, следовательно, произведение данных матриц определено и в результате получится матрица размерности 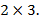
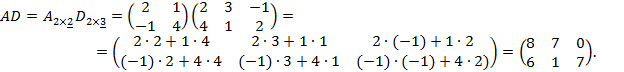
Перемножим теперь матрицы  Внутренние индексы совпадают, следовательно, произведение данных матриц определено и в результате получится матрица размерности
Внутренние индексы совпадают, следовательно, произведение данных матриц определено и в результате получится матрица размерности 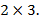
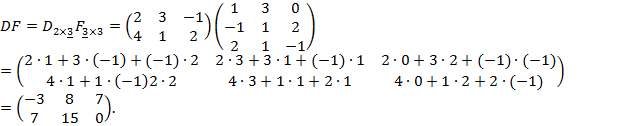
Перемножим теперь матрицы 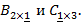 Внутренние индексы совпадают, следовательно, произведение данных матриц определено и в результате получится матрица размерности
Внутренние индексы совпадают, следовательно, произведение данных матриц определено и в результате получится матрица размерности 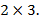

Перемножим теперь матрицы 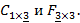 Внутренние индексы совпадают, следовательно, произведение данных матриц определено и в результате получится матрица размерности
Внутренние индексы совпадают, следовательно, произведение данных матриц определено и в результате получится матрица размерности 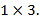
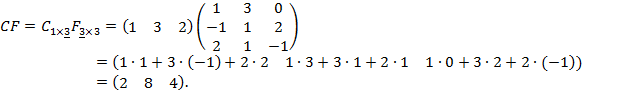
3. Для данной матрицы
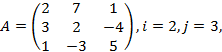
вычислить определитель:
1) методом параллельного переноса;
2) методом треугольников;
3) разложением по  -ой строке и по
-ой строке и по 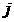 -му столбцу;
-му столбцу;
4) вычислить, получив нулевые элементы в первом столбце используя элементарные преобразования со строками;
5) вычислить обратную матрицу 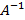 и проверить равенство
и проверить равенство 
Решение.
1) Согласно правила параллельного переноса, допишем к нашему определителю две первые строки и выполним необходимые действия:
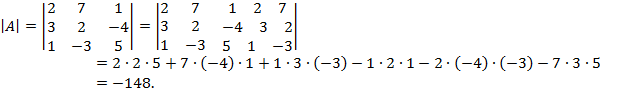
2)вычислим определитель методом треугольников:
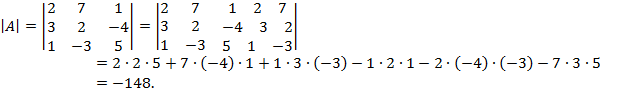
3) вычислим определитель разложением по элементам 2-ой строки:
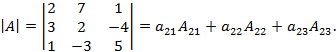
Выпишем алгебраические дополнения и вычислим их:
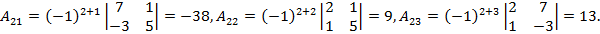
Наше разложение по второй строке имеет вид:

Разложением по элементам 3-его столбца:
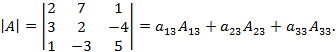
Аналогично предыдущего пункта записываем миноры, вычисляем их, получаем:
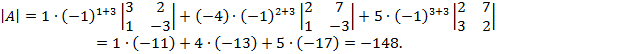
4) Используя элементарные преобразования со строками, получим нулевые элементы в первом столбце. Для этого:
1) умножим третью строку на 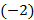 и прибавим к первой строке,
и прибавим к первой строке,
2) умножим третью строку на 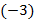 и прибавим ко второй строке.
и прибавим ко второй строке.
Получили определитель эквивалентный исходному

Полученный определитель разложим по элементам первого столбца
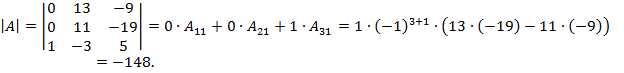
4. Вычислить матрицу, обратнуюк данной
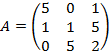
и проверить равенство 
Решение.
Вычислим определитель матрицы:
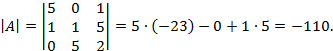
Т.к. определитель отличен от нуля, то матрица не является вырожденной и для нее определена обратная матрица. Для её нахождения протранспонируем матрицу 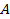 и вычислим её алгебраические дополнения
и вычислим её алгебраические дополнения
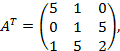
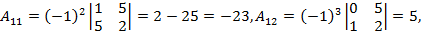
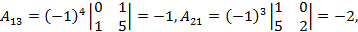

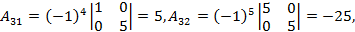
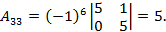
Присоединенная матрица:
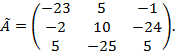
Тогда обратная матрица запишется в виде:
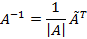

Сделаем проверку и убедимся, что 

Обратная матрица вычислена верно.
Дата добавления: 2018-04-15; просмотров: 2088; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
