Теорема про криві нульової кривини.
Теорема. Для того, щоб крива була прямою або її частиною (відрізком, променем), необхідно і достатньо щоб у кожній її точці кривина дорівнювала нулю.
Теорема про криві нульового скруту.
Теорема. Для того, щоб крива була плоскою, необхідно і достатньо, щоб у кожній її точці скрут дорівнював нулю.
Основна терема теорії кривих.
Теорема( основна теорема теорії кривих). Нехай на множині 
задані функції 
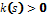й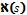 
класів 
і 
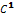відповідно. Тоді існує єдина ( з точністю до положення в просторі) регулярна крива, для якої 
і 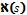є відповідно кривиною та скрутом в точці, яка відповідає значенню параметра 
.
Означення векторної функції двох скалярних аргументів. Диференціювання векторної функції.
Вектором-функцією двох аргументів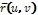 
заданою на 
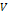, називається відображення, при якому кожній парі 
відповідає вектор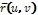
простору 
.
Невелика відмінність стосується диференціювання. Замість однієї похідної у вектора-функції двох аргументів є дві частині похідні, які будемо позначати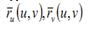 
або 
, або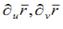 
.
Поняття параметризованої поверхні. Регулярність поверхні. Приклади.
Нехай V - деяка область на площині R2 з декартовими координатами u , v . Параметризованою поверхнею називається неперервне відображення з області V в простір E3, при якому кожній парі (u,v) є V відповідає точка простору E. Змінні, u,v називаються параметрами поверхні. Образ області V називається образом або носієм поверхні.
|
|
|
Якщо виконується умова [ru,rv]≠0, то поверхня називається регулярною.
Нехай крива f: c(t)=(u(t),v(t)) , що задана в області V, регулярна. Тоді її образ на регулярній поверхні F : r = r (u,v), (u,v) є V також є регулярною кривою. Це так, тому що
вектор-функція R(t)=(u(t),v(t)), що задає образ регулярної кривої l на поверхні F, регулярна як складна функція двох регулярних функцій r (u,v), c(t).
Криволінійні координати, координати лінії поверхні. Завдання кривої на поверхні.
Криві на поверхні r = r (u,v), що мають внутрішні рівняння u=t, v=v0=const, й v=t, u=u0=const, називаються координатними лініями. Координатні лінії регулярної поверхні утворюють дві сім’ї регулярних кривих.
Нехай r = r (u,v) – векторне рівняння регулярної поверхні. u=u(t), v=v(t) – внутрішні рівняння кривої γ : t є R → (u(t),v(t)) - r(u(t),v(t))
Таким чином в реультаті композиції, кожному t ставиться у відповідність r(u(t),v(t))= R(t).
Т.к. R(t) – векторна функція одного скалярного аргумента, то ми отримаємо криву в просторі R2.
Дотична площина та нормаль параметризованої поверхні. Їх рівняння.
Площина, що проходить через точку M0 поверхні F й містить всі дотичні прямі до всіх регулярних кривих поверхні, що проходять через цю точку, називається дотичною площиною поверхні в даній точці. Позначають TМ0F. Нормаллю регулярної поверхні в даній її точці називається пряма, що проходить через цю точку й перпендикулярна дотичній площині поверхні в даній точці Дотична площина визначається точкою М0(u0,v0), й направляючим бівектором [ ru(u0,v0), rv(u0,v0)]. Рівняння дотичної площини та нормалі мають відповідно вигляд
|
|
|
α(x-x0) + β(y-y0) – γ(z-z0) = 0,
(x-x0)/α + (y-y0)/β – (z-z0)/γ = 0,
Де α,β,γ – координати вектора [ru,rv](M0).
Дата добавления: 2018-04-15; просмотров: 243; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!