Стична площина кривої. Теорема про стичну площину.
Векторна функція одного скалярного аргументу. Означення та приклади. Границя та неперервність векторної функції.
Векторною функцією  (вектор – функцією
(вектор – функцією  ), заданою на множині
), заданою на множині  , називається відображення, при якому кожному значенню
, називається відображення, при якому кожному значенню 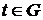 відповідає вектор
відповідає вектор  простору
простору 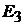 .
. 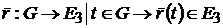 .Постійний вектор
.Постійний вектор 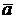 називається границею векторної функції
називається границею векторної функції  при
при  , якщо для кожного
, якщо для кожного  існує
існує  таке, що для всіх
таке, що для всіх 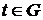 , які задовольняють умові
, які задовольняють умові 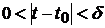 , виконується нерівність
, виконується нерівність 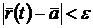 . Позначають:
. Позначають: 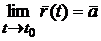 . Векторна функція
. Векторна функція  називається неперервною в точці
називається неперервною в точці 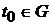 , якщо
, якщо  . Якщо векторна функція
. Якщо векторна функція  неперервна в усіх точках множини
неперервна в усіх точках множини  , то вона називається неперервною на цій множині.
, то вона називається неперервною на цій множині.
Диференційованість векторної функції. Теорема про властивості диференційованих векторних функцій та наслідки з неї. Диференціювання складної векторної функції одного аргументу. Формула Тейлора.
Векторна функція  називається диференційованою в точці
називається диференційованою в точці 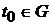 , якщо при
, якщо при 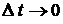 існує границя відношення
існує границя відношення 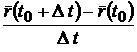 .
.
(властивості диференційованих функцій). Якщо векторні функції  ,
,  ,
, 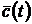 і скалярна функція
і скалярна функція 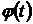 диференційовані в точці
диференційовані в точці 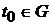 , то в цій точці диференційовані функції
, то в цій точці диференційовані функції 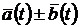 ,
, 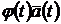 ,
, 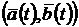 ,
, 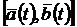 ,
, 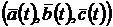 і мають місце рівності
і мають місце рівності
1.  ,
,
2. 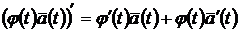 ,
,
3. 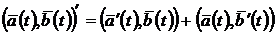 ,
,
4. 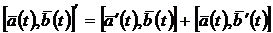 .
.
5. 
(правило диференціювання складної функції). Нехай скалярна функція 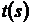 диференційована в точці
диференційована в точці 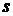 , а векторна функція
, а векторна функція  диференційована в точці
диференційована в точці 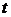 . Тоді складна функція
. Тоді складна функція 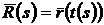 диференційована в точці
диференційована в точці 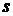 , причому
, причому 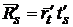 .
.
(формула Tейлора). Якщо векторна функція 
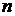 раз диференційована в точці
раз диференційована в точці 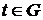 й
й 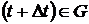 , то
, то
|
|
|
 ,
,
де  .
.
Поняття кривої. Способи завдання. Регулярність кривої. Особливі точки.
Параметризованой кривой наз. неп. отобр. γ :I→E3, при котором ∀ tϵI соотв. т. MϵE3 Кривой наз.годограф неп.векторной.фун-ии. Кривая задана при помощи вектор.функ-ии 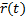 наз.гладкой кривой класса ck , если
наз.гладкой кривой класса ck , если 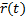 имеет неп.производные до порядка k включительно. Задаются явно, неявно, параметрически. Кривая наз.регалярной, если для любой ее т.при переходящем выборе прямоугольной декартовой сист.координ. x,y,z она допускает в окр.этой точки задание уравнениями y=y(x), z=z(x). Особливі точки кривої - будь-яка точки кривої, що не є реґулярними.
имеет неп.производные до порядка k включительно. Задаются явно, неявно, параметрически. Кривая наз.регалярной, если для любой ее т.при переходящем выборе прямоугольной декартовой сист.координ. x,y,z она допускает в окр.этой точки задание уравнениями y=y(x), z=z(x). Особливі точки кривої - будь-яка точки кривої, що не є реґулярними.
Заміна параметра на кривій. Властивість допустимої заміни.
Замена параметра на кривой при помощи фан-ии τ=τ(t) наз.допустимой, если ∀t∈I 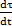 ≠
≠ 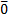 -доп.замена параметра. Доп.замена параметра на кривой сохранаяет свойство регулярности.
-доп.замена параметра. Доп.замена параметра на кривой сохранаяет свойство регулярности.
Неявне завдання кривої. Теорема про неявно задану криву.
Кривая задана неявно, если её декартовы координаты удовлетворяют систему: 
Теорема. Пусть 𝜔-мн-во т.простор.E3 удовл.сист.(1). М0(x0,y0,z0)∈𝜔 и для неё выполняется условие  ,тогда сущ.окресность
,тогда сущ.окресность 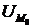 т.M0 такая что пересечение
т.M0 такая что пересечение 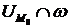 -регул.параметризованная кривая.
-регул.параметризованная кривая.
|
|
|
Дотична пряма та нормальна площина неявно заданої кривої.
Пусть F и Ф заданы неявным уравнением кривой, диференцируемые в неособой т.М0(x0,y0,z0) этой кривой, тогда 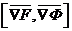 явл.направляющим вектором касательной прямой в т.М0.
явл.направляющим вектором касательной прямой в т.М0.
Нормальной плоскостью кривой в т.М0 наз.плоскость проход.через эту точку и перпендикулярная касательной прямой в т.М0.
Стична площина кривої. Теорема про стичну площину.
Стичною площиною просторової кривої в даній її точці 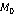 називається граничне положення, до якого прагне січна площина (
називається граничне положення, до якого прагне січна площина ( 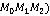 , за умови, що точки M1 й M2 прагнуть по кривій до точки
, за умови, що точки M1 й M2 прагнуть по кривій до точки 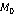 .
.
Теорема. Усяка крива в будь-якій своїй бірегулярній точці 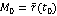 має стичну площину, нормальним вектором якої є вектор [
має стичну площину, нормальним вектором якої є вектор [ 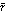 ’(
’( 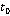 ),
), 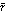 ’’(
’’( 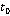 )].
)].
Дата добавления: 2018-04-15; просмотров: 491; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
