Оценка качества регулирования в установившемся режиме

При изменении воздействия g(t)на входе системы (рис. 1) выходную величину х(t)можно записать так:

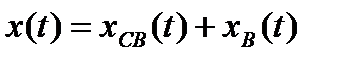(4.1)

где 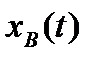— решение дифференциального уравнения, описывающего систему; 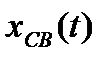— свободная составляющая переходного процесса, соответствующая общему решению однородного дифференциального уравнения.

X(t)

W(s)

ε(t)

g(t)

Рис. 4.1. Система автоматического регулирования.

Если последнее не имеет кратных корней, то

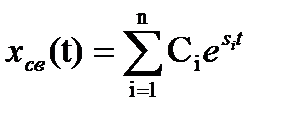, (4.2)

гдеС_i— постоянная интегрирования, значение которой определяют параметры системы и начальные условия; s_i— корни характеристического уравнения замкнутой системы D(s) = 0;

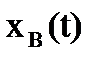- вынужденная составляющая переходного процесса, обусловленная законом изменения g(t).

Из (4.1) видно, что качество переходного процесса можно оценить по его составляющим 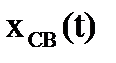и .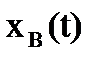

Рассмотрим показатели качества, характеризующие вынужденную составляющую ошибки 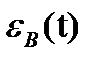системы. Если на входе системы (рис. 4.1) действует сигнал g(t),то установившаяся ошибка регулирования системы ,(4.3)

где 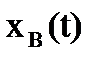— вынужденная составляющая регулируемой величины (4.1).

Если g(t)дифференцируема во всем интервале 0 ≤ t ≤ ∞, то ошибка системы 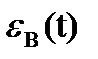может быть представлена в виде ряда:

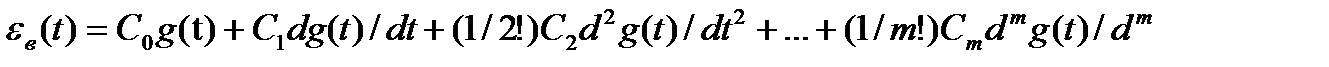, (4.4)

где коэффициенты 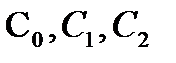, ... принято называть коэффициентами ошибок. Формула (4.4) получена следующим образом.

Передаточная функция замкнутой системы относительно ошибки (рис. 4.1)

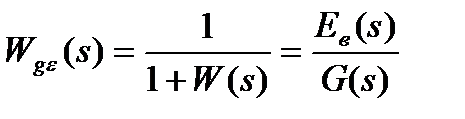(4.5)

Из (4.5) можно найти выражение для изображения ошибки:

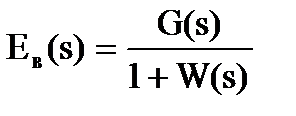(4.6)

Разложим передаточную функцию по ошибке 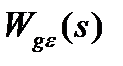(4.5) в ряд по возрастающим степеням s в окрестности точки ε = 0, что соответствует большим значениям времени (t → ∞), т. е. значению установившейся ошибки при заданном управляющем воздействии.

В соответствии с (4.6) можно записать

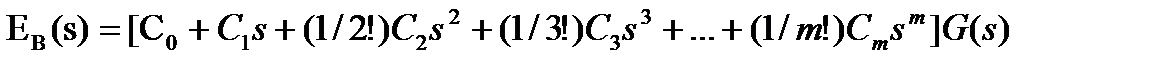(4.7)

Если передаточная функция 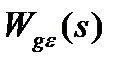является дробно-рациональной функцией

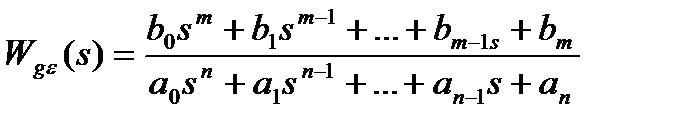(4.8)

то разложение в ряд 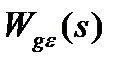можно осуществить делением числителя на знаменатель, располагая члены полинома в порядке возрастания степеней. Переходя в (4.7) от изображений к оригиналам, можно получить для ε_в(t)выражение (4.4). Коэффициенты ошибок 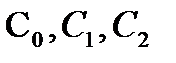, ... определяют по формулам разложения функции 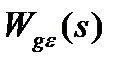в ряд Тейлора:

;

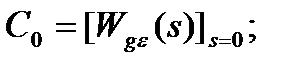
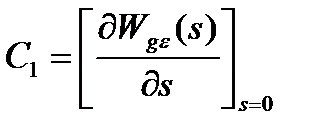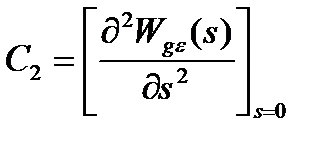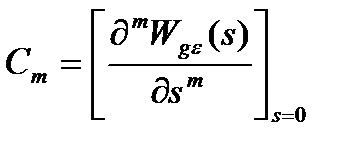; …….. . (4.9)

Если g(t)=1(t),то все производные: 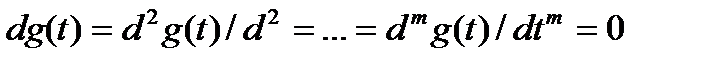, (4.10)

тогда:

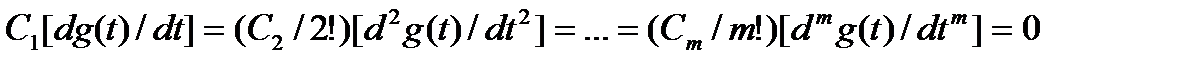, (4.11)

В данном случае 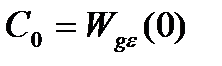— значение установившейся ошибки в замкнутой системе.

Если g(t) = t, то dg(t)/dt = 1, а

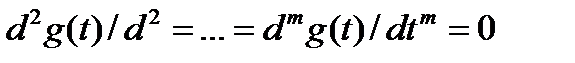, (4.12)

токоэффициенты: 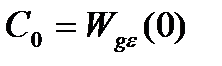; ; 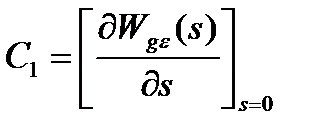а

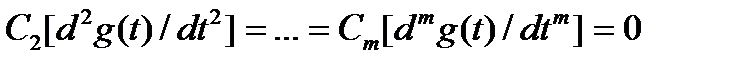(4.13)

и т. д.

Коэффициент 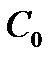называют коэффициентом статической или позиционной ошибки; коэффициент 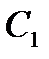— коэффициентом скоростной ошибки, 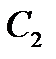— коэффициентом ошибки от ускорения.

Оценка качества переходного процесса при воздействии ступенчатой функции

Прямые оценки качества получают по кривой переходной характеристики h(t),т. е. при воздействии единичной ступенчатой функции и нулевых начальных условиях.

Эту характеристику можно построить для выходной величины или для отклонения 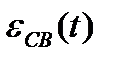(рис. 4.3, а, б).

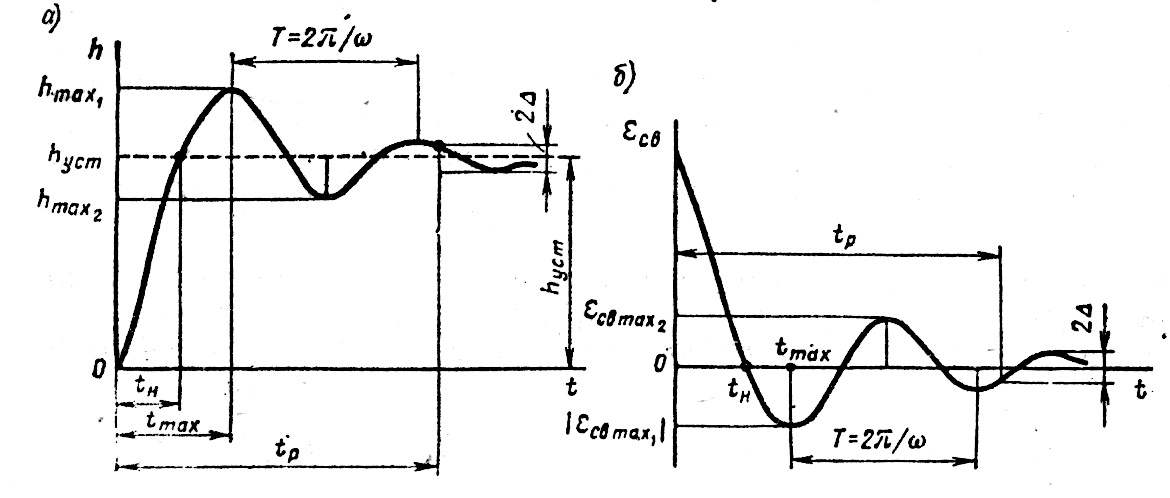
Рис. 4.3. Переходная характеристика h(t) (а) и переходная характеристика для отклонения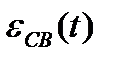

К прямым оценкам качества относят:

1.Время регулирования 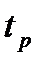— минимальное время, по истечении которого регулируемая величина будет оставаться близкой к установившемуся значению с заданной точностью

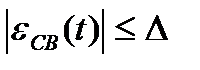
(4.27)

или

, (4.28)

где ∆ — постоянная величина, значение которой нужно оговаривать (задается величина ∆ в процентах от установившегося значения выходной величины ).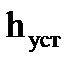

2.Перерегулирование σ— максимальное отклонение переходной характеристики от установившегося значения выходной величины, выраженное в относительных единицах или процентах:

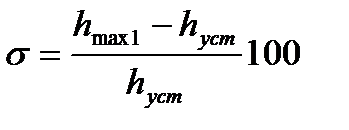, (4.29)

где — значение первого максимума, или

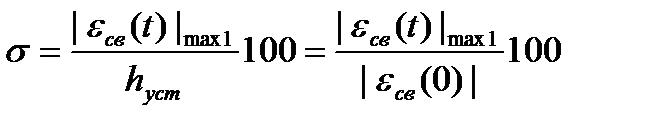. (4.30)

3.Частоту колебаний 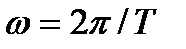,где Т — период колебаний для колебательных переходных характеристик.

4.Число колебаний n, которое имеет переходная характеристика 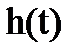или 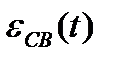за время регулирования .

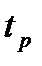5.Время достижения первого максимума .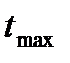

6.Время нарастания переходного процесса 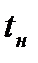— абсциссу первой точки пересечения кривой переходной характеристики h(t)с уровнем установившегося значения 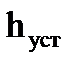или кривой отклонения 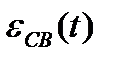с осью абсцисс.

7. Декремент затухания 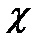, равный отношению модулей двух смежных перерегулирований:

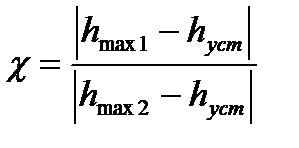(4.31)

Определение приведенных выше прямых оценок качества переходного процесса проиллюстрировано на рис. 4.3,а, б.

Переходные процессы, возникающие в системах при скачкообразных воздействиях, принято делить на три группы: монотонные, апериодические и колебательные. У монотонных процессов первая производная выходной величины 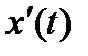не меняет знак (кривая ана рис. 4.4), у апериодических знак производной 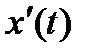меняется не более одного раза (кривая бна рис. 4.4), а у колебательных —первая производная 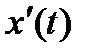меняет свой знак периодически (теоретически бесконечное число раз) (кривая вна рис. 4.4).

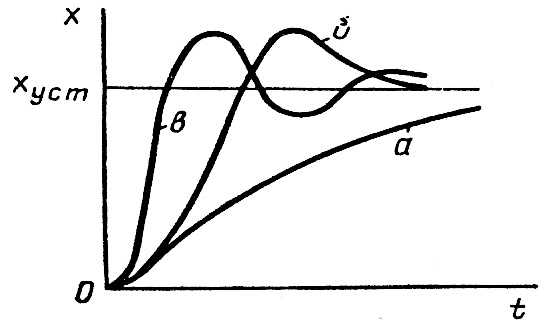
Рис.4.4. Типы переходных процессов.

Среднегеометрический корень

Пусть характеристическое уравнение системы имеет вид

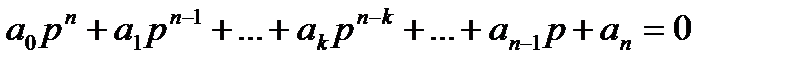, (4.60)

гдер = с + jω — комплексное число.

Используя понятиесреднегеометрического корня

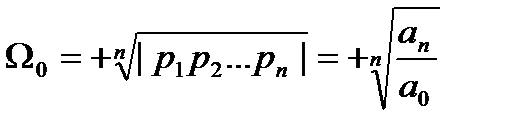, (4.61)

гдеp_l, р₂, . . ., р_n— корни характеристического уравнения, в формуле (15) можно перейти к новой комплексной величине qпутем подстановки р = Ω₀q. В результате получим уравнение

, (4.62)

в котором безразмерные коэффициенты А₁, А₂, ., A_k, . . ., А_n_-1определяются выражением

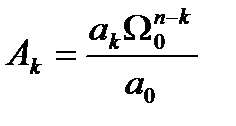(4.63)

а его корни равны 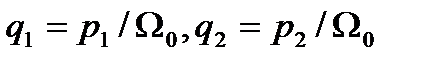…. и т. д.

Исходное характеристическое уравнение (4.60)при возвращении к прежней комплексной величине получает вид

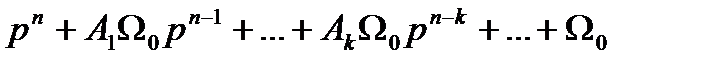(4.64)

Среднегеометрический корень 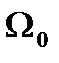может служить мерой быстроты протекания переходных процессов. Если в уравнении (4.64) увеличить 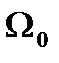,например, в 10 раз, то на основании теоремы подобия переходный процесс, оставаясь подобным сам себе, будет протекать в 10 раз быстрее. В связи с этим можно рассматривать (4.62) как некоторое нормированное характеристическое уравнение, которому соответствует переходный процесс, построенный для безразмерного времени .

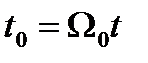Для увеличения величины 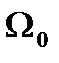, как следует из (4.61), необходимо увеличивать свободный член характеристического уравнения 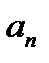. Напомним, что в статических системах 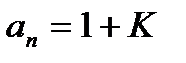,а в астатических 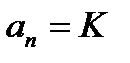,где К— общий коэффициент усиления по разомкнутой цепи регулирования. Следовательно, повышение быстродействия может осуществляться за счет увеличения общего коэффициента усиления.

Диаграмма Вышнеградского

Рассмотрим характеристическое уравнение третьего порядка:

(4.65)

Приведем его к нормированному виду. Для этого разделим все члены на а₃и введем новую переменную

(4.66)

Здесь использовано понятие среднегеометрического корня:

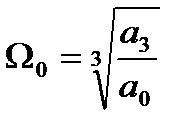
В результате получим нормированное уравнение

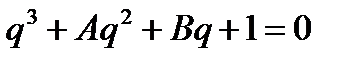, (4.67)

где коэффициенты:

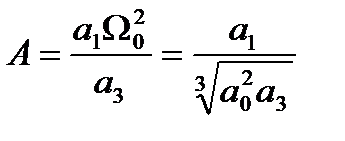
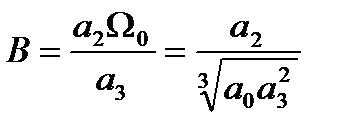(4.68)

называютсяпараметрами Вышнеградского.

На плоскости параметров Аи Внанесем границу устойчивости. Условия: А> 0, В> 0 и АВ> 1. Уравнение границы устойчивости (колебательной): АВ= 1 при А> 0 и В>0. Это есть равнобокая гипербола, для которой оси координат служат асимптотами (рис. 4.7).

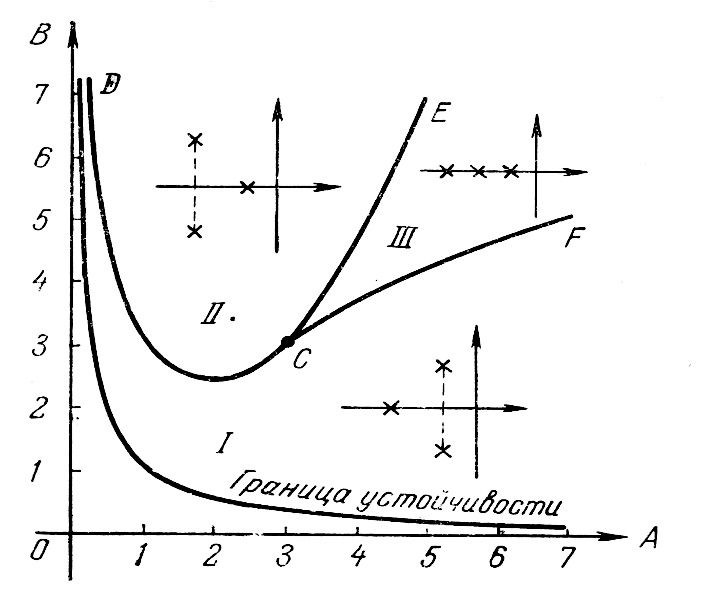
Рис. 4.7. Диаграмма Вышнеградского.

Область устойчивости системы, согласно написанным выше условиям, лежит выше этой кривой.

Разобьем область устойчивости на отдельные части, соответствующие различному расположению корней характеристического уравнения. Заметим, что в точке С,где А= 3 и В= 3, характеристическое уравнение (3) принимает вид 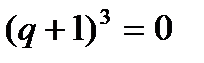. Следовательно, в этой точке все три корня равны: . При этом для исходного характеристического уравнения согласно (2) получаем:

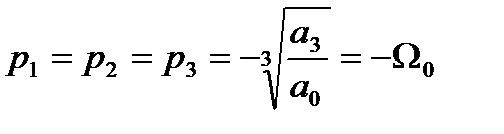. (4.69)

В общем случае возможны два варианта:

1) все три корня вещественные;

2) один корень вещественный и два комплексных.

Граница между этими двумя случаями определяется равенством нулю дискриминанта уравнения третьей степени (4.67), который может быть получен, например, из формулы Кардана для решения кубического уравнения

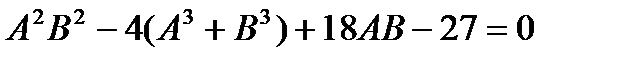Это уравнение дает на плоскости параметров А,Вдве кривые: СЕи CF(рис. 4.7). Внутри области ECFдискриминант положителен. Следовательно, в этой области имеется три вещественных корня (область III). В остальной части плоскости дискриминант отрицателен, что соответствует наличию пары комплексных корней.

Существенное значение имеет взаимное расположение вещественного и комплексных корней. Будем различать здесь два случая: I — пара комплексных корней лежит ближе к мнимой оси, чем вещественный. II — вещественный корень лежит ближе к мнимой оси, чем пара комплексных. Границей между этими двумя случаями является расположение всех трех корней на одинаковом расстоянии от мнимой оси. Уравнение этой границы можно найти, положив значения корне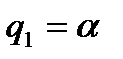й и 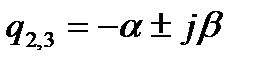. Тогда характеристическое уравнение (4.67) будет

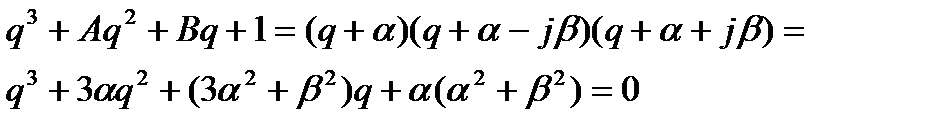(4.70)

Уравнивание коэффициентов при одинаковых степенях дает

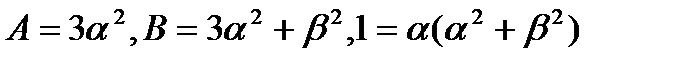(4.71)

В результате совместного решения последних трех равенств получаем после исключения αи β искомое уравнение, соответствующее граничному случаю:

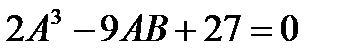, A< 3. (4.72)

Написанное равенство дает на плоскости параметров кривую CD.

В результате область устойчивости разбивается на три части: I, II, III(рис. 4.7). Этот график называется диаграммой Вышнеградского.

В области III,где все корни вещественные, в зависимости от начальных условий получим апериодический переходный процесс в одной из форм, показанных на третьем графике рис. 4.8. ОбластьIIIносит название области апериодических процессов.

В областях Iи II, где имеется один вещественный корень и два комплексных, переходный процесс будет иметь соответственно формы, показанные на первых двух графиках рис. 4.8. В области I быстрее затухает экспонента и переходный процесс в основном будет определяться колебательной составляющей. Это будет область колебательных процессов. В области II, наоборот, быстрее затухает колебательная составляющая. Это будет область монотонных процессов.

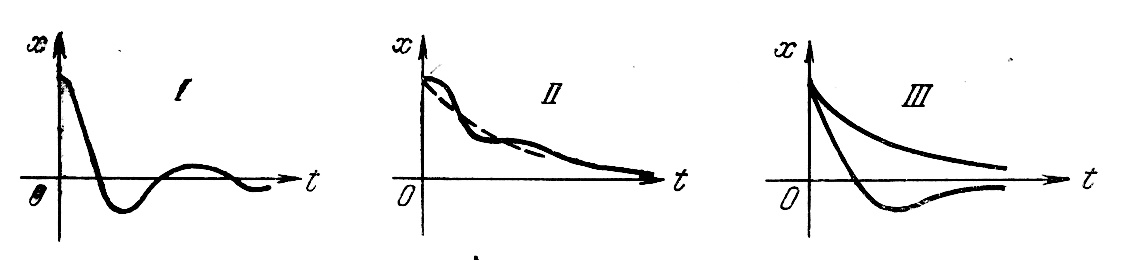
Рис. 4.8. Вид переходных процессов

Дата добавления: 2018-04-05; просмотров: 1221; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 6 7 8 9 10 11 12 13 1415

Мы поможем в написании ваших работ!