D-разбиение по одному(комплексному) параметру

 

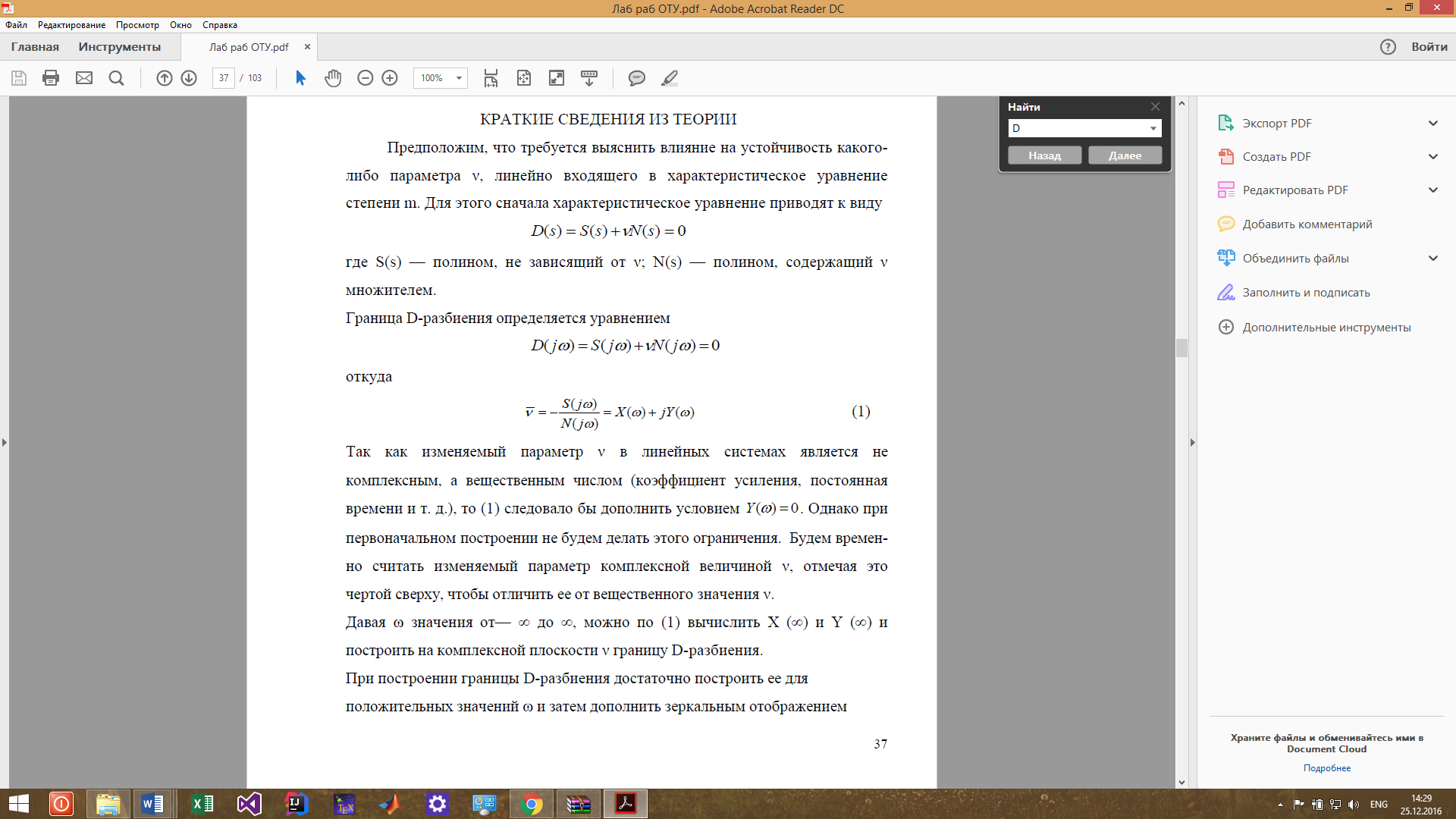
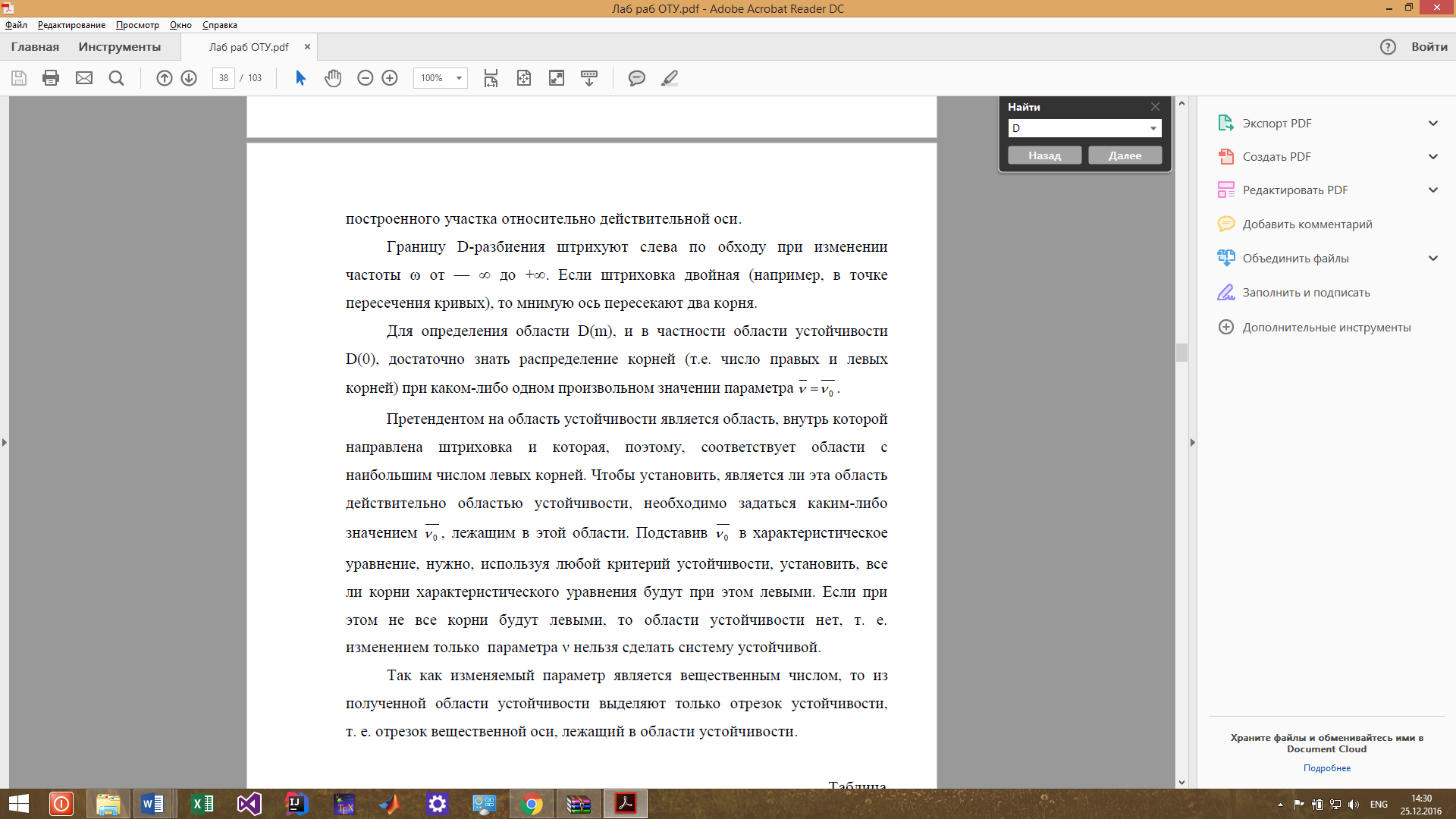
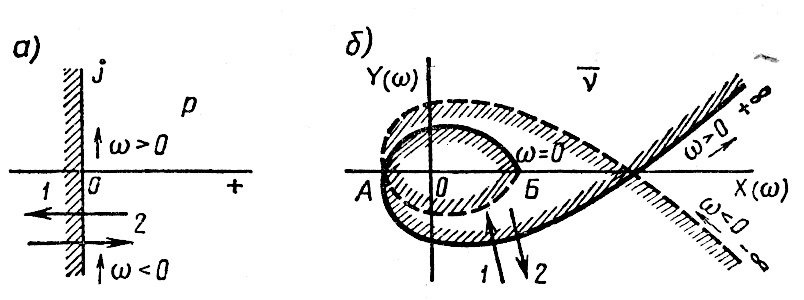
                            Рис. 3.30. Построение границы D-разбиения

 

Отрезок АБ лежит в области устойчивости

 

 

 

Устойчивость систем с запаздыванием

Системы автоматического управления могут содержать звенья, и которых зависимость между входной u(t)и выход­ной у(t)величинами имеет вид

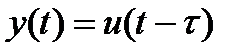                                     (3.145)

где 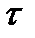 — постоянная величина, называемая временем запазды­вания. Такие звенья называют запаздывающими, так как они воспроизводят изменения входной величины без искажения, но с некоторым постоянным запаздыванием .

Передаточная функция запаздывающего звена:

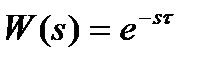                                        (3.146)

Системы, содержащие звенья с распределен­ным запаздыванием, требуют для своего описания дифференциальных уравнений в частных производных.

 

Структурная схема одноконтурной системы автоматическо­го управления, содержащей одно запаздывающее звено, может быть представлена либо так, как показано на рис. 3.32 а, а,если запаздывающее звено находится в прямой цепи, либо так, как показано на рис. 3.32 б, если запаздывающее звено нахо­дится в цепи обратной связи.

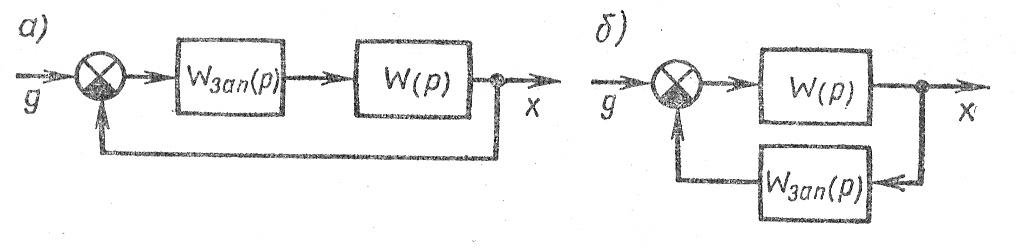
                  Рис.3.32. Структурная схема САУ с звеном запаздывания

 

Передаточная функция разомкнутой системы с запаздыва­нием равна

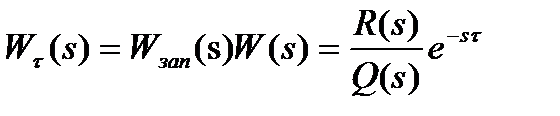                    (3)

гдеW(s) — R(s)/Q(s)— передаточная функция разомкнутой системы без учета запаздывания, представляющая собой дроб­но-рациональную функцию оператора s.

Если запаздывающее звено находится в прямой цепи, то передаточная функция замкнутой системы

                      (3.148)

Если же запаздывающее звено находится в цепи обратной связи, то передаточная функция замкнутой системы

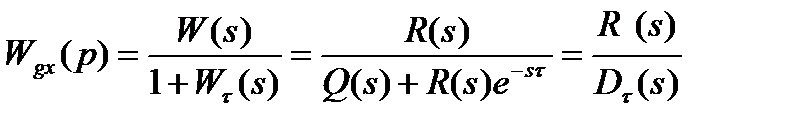                       (3.149)

характеристическое уравнение сис­темы с запаздыванием имеет вид

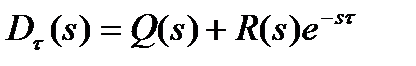(6)

Это характеристическое уравнение из-за наличия множите­ля является не полиномом, а трансцендентной функцией оператора s и в отличие от обыкновенного алгебраического уравнения имеет бесконечное множество корней. Так как

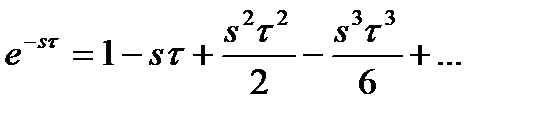                           (3.151)

то (6) можно рассматривать как уравнение «бесконечной степени».

Для того чтобы линейная система с постоянным запазды­ванием была устойчива, необходимо и достаточно, чтобы все корни уравнения (6) были левыми.

Для исследования устойчивости систем с запаздыванием можно применять основанные на принципе аргумента частот­ные критерии устойчивости Михайлова и Найквиста либо ме­тод D-разбиения.

Уравнение кривой (годографа) Михайлова системы с запаз­дыванием получают после подстановки s= jω в характеристи­ческое уравнение (6), т. е.

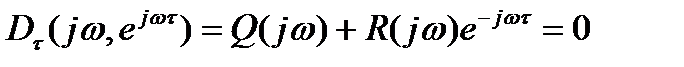(7)

Для исследования устойчивости систем с запаздыванием очень удобно применять критерий устойчивости Найквиста.

Формулировка критерия устойчивости Найквиста для систем с запаздыва­нием в этом случае аналогична формулировке для обычных систем, имеющих дробно-рациональные передаточные функции.

Частотную передаточную функцию 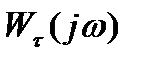разомкнутой системы с запаздыванием находят, подставляя s =jω в (3):

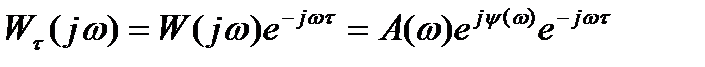(3.153)

гдеW(jω) = U(ω) + jV(ω) — амплитудно-фазовая харак­теристика разомкнутой системы без учета запаздывания;

—амплитудно-частотная характеристика;

-фазочастотнаяха­рактеристика разомкнутой системы без учета запаздывания;

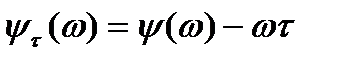     (3.154)

— фазочастотная характеристика разомкнутой системы с за­паздыванием.

Из (8) и (9) видно, что наличие запаздывающего зве­на не меняет модуля А(ω) амплитудно-фазовой характери­стики разомкнутой системы 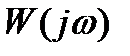, а вносит лишь дополни­тельный отрицательный фазовый сдвиг 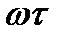, пропорциональный частоте, причем коэффициентом пропорциональности являет­ся время запаздывания .

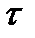Зная амплитудно-фазовую характеристику 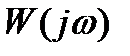 разом­кнутой системы без запаздывания, легко построить амплитуд­но-фазовую характеристику 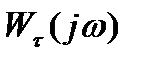разомкнутой системы с за­паздыванием. Для этого каждый модуль А(ω_i) вектора ам­плитудно-фазовой характеристики  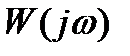нужно повернуть на угол 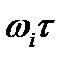по часовой стрелке. С ростом частоты ωугол будет быстро расти, а модуль А(ω) обычно уменьшается, по­этому амплитудно-фазовая характеристика 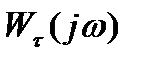разомкну­той системы с запаздыванием имеет вид спирали, закручиваю­щейся вокруг начала координат (рис. 3.33).

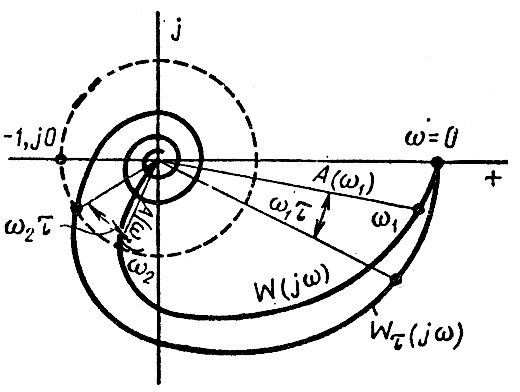
                 Рис. 3.33. АФЧХ разомкну­той системы с запаздыванием

 

«Закручивание» амплитудно-фазовой характеристики из-за наличия дополни­тельного фазового сдвига ωτ, вообще говоря, ухудшает усло­вие устойчивости, так как вся амплитудно-фазовая характе­ристика приближается к критической точке (—1, j0). Однако иногда при сложной форме амплитудно-фазовой характери­стики  введение постоянного запаздывания может улуч­шить условия устойчивости.

Изменяя время запаздыва­ния τ в широких пределах, можно найти такое его зна­чение, при котором замкну­тая система будет находить­ся на границе устойчивости. В этом случае характери­стика 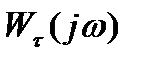будет прохо­дить через точку (—1, j0). Время запаздывания 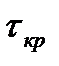и соответствующее ему значе­ние частотыω_кр, при которых 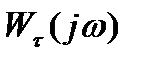проходит через точку (—1,j0), называют крити­ческими.

Для критического случая справедливо следующее условие:

        (3.155)

Условие (10) можно записать раздельно для амплитуд и фаз вектора, :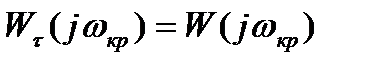

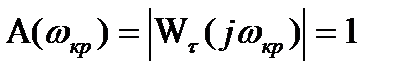;                                  (3.156)

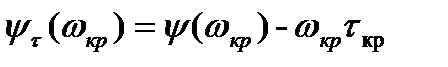,                            (3.157)

где i = 0, 1, 2, 3, ...  

Из (11) можно найти сначала ω_кр, а затем из (12) найти τ_кр, т. е.

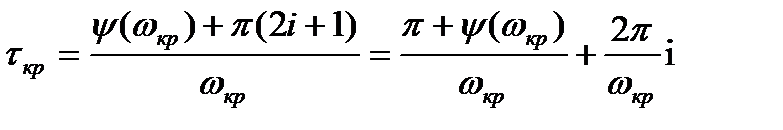                   (3.158)

Для систем автоматического управления с запаздыванием основное значение имеет минимальное критическое время за­паздывания(при i= 0), которое является в то же время и граничным

 ,                     (3.159)

где 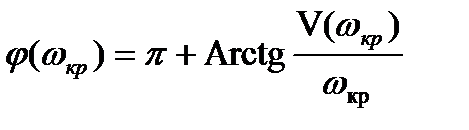 - запас устойчивости по фазе

При сложном выражении для частотной передаточной функ­ции W(jω) разомкнутой системы определение критического времени запаздывания просто выполнить графически. Условие 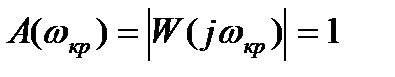определяется пересечением годо­графа W(jω) с окружностью единичного радиуса с центром в начале координат (рис. 3.34). Точка пересечения определяет одновременно 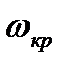и угол 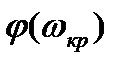, который, будучи разделен на 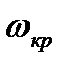, даст значение критического времени запаздывания.

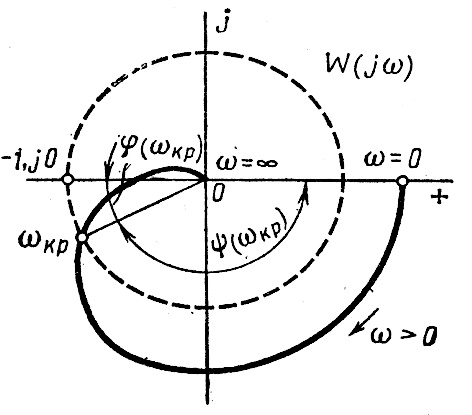
       Рис. 3.34. Определение критического времени запаздывания.

 

Если имеется несколько точек пересечения годографа W(jω) с окружностью единичного радиуса, например при 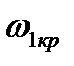, , 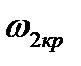        (рис. 3.35), то система будет иметь несколь­ко критических граничных времен запаздывания:

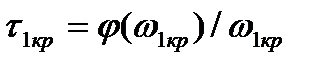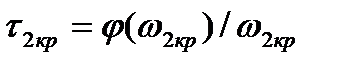; ;  . (3.160)

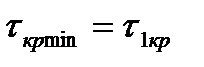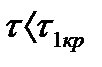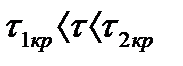причем минимальное время запаздывания равно . Система будет устойчива при , а также при . Система будет неустойчива при , а также при  . Наблюдаемое в этом случае чередование участков устойчивости и неустойчивости системы при непрерывном изменении 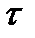 (а также других параметров си­стемы) является характерной особенностью многих систем с постоянным запаздыванием.

Обычно для повышения быстродействия и точности систе­мы время запаздывания 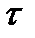стремятся уменьшить, поэтому кри­терий устойчивости формулируется лишь для минимального времени запаздывания.

Система автоматического управления будет устойчива, если время запаздывания 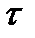меньше минимального критическо­го времени запаздывания: .

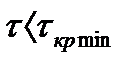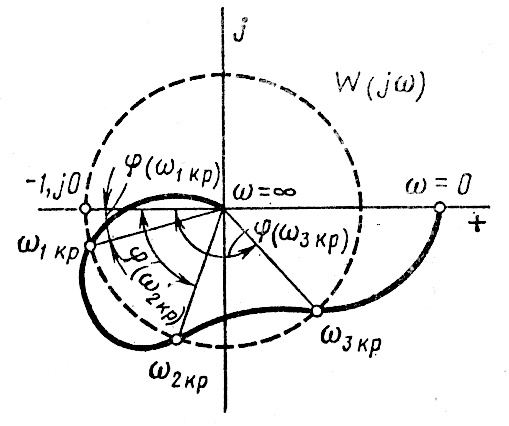
Рис. 3.35. Определение нескольких критических времен запаздывания

 

 

---

Дата добавления: 2018-04-05; просмотров: 684; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!