Химическая термодинамика. Основные понятия термодинамики: термодинамическая система, процесс, фаза, компонент параметры состояния, функции состояния и их уравнения
ПРОЦЕСС (от лат. processus - продвижение) - 1) последовательная смена явлений, состояний в развитии чего-нибудь.
Теплота, работа, термодинамическая система, параметры и уравнение состояния?, открытая, закрытая и изолированная системы
Фазой называется термодинамически равновесное состояние вещества, отличающееся по физическим свойствам от других возможных равновесных состояний того же вещества.
Компонент– химически индивидуальные вещества, наименьшего числа которых достаточно для образования всех фаз, т. е. гомогенных частей данной системы.
Системой называют отдельное тело или группу тел, фактически или мысленно отделенных от окружающей среды.Систему называют термодинамической, если между телами ее составляющими может происходить обмен теплотой, веществом, и если система полностью описывается термодинамическими параметрами (кипящий чайник).
Открытая термодинамическая система – это такая система, которая может обмениваться с окружающей средой энергией и веществом, (например, кипящий чайник).
Закрытой системой называют систему, которая не может обмениваться веществом с окружающей средой, но может обмениваться теплотой и работой. ( плотно закрытая колба с раствором, которая нагревается или охлаждается окружающей средой.)
Изолированной термодинамической системой называют систему, не имеющую обмена веществом и энергией с окружающей средой. Внутри системы может происходить передача теплоты от более нагретой части системы к более холодной, взаимное превращение энергий, выравнивание концентраций, однако внутренняя энергия системы остается постоянной. Примером такой системы является химическая реакция, идущая в термостате.
|
|
|
Основными параметрами состояния системы называются параметры, которые измеряются напрямую и определяются экспериментально. Это температура, давление, теплоемкость, концентрация.
Зависимость между параметрами состояния термодинамической системы выражается уравнением состояния, которое позволяет определять одни параметры состояния через другие. Если состояние системы может быть полностью описано с помощью трех параметров: давления 
, объема 
и температуры 
, тоуравнение состояния в самом общем виде будет иметь форму
|
Обобщение многочисленных экспериментальных данных показывает, что большинство газов при комнатной температуре и давлении порядка одной атмосферы (при нормальных условиях) с достаточно высокой точностью могут быть описаны уравнением состояния, называемым уравнением Клапейрона-Менделеева:
 ,
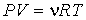| (2.2) |
где: P- давление газа,V- занимаемый им объем, ν- количество молей газа,R- универсальная газовая постоянная,T- абсолютная температура.
|
|
|
2.Закон Рауля. Криоскопический метод определения молекулярной массы. Изотонический коэффициент. 29. Понятие идеального раствора.
Первый закон Рауля:
Парциальное давление насыщенного пара компонента раствора прямо пропорционально его мольной доле в растворе, причём коэффициент пропорциональности равен давлению насыщенного пара над чистым компонентом.
Для бинарного раствора, состоящего из компонентов А и В (компонент А считаем растворителем) удобнее использовать другую формулировку:
Относительное понижение парциального давления пара растворителя над раствором не зависит от природы растворённого вещества и равно его мольной доле в растворе.
Предельно разбавленный раствор получают путем последовательного разбавления исследуемого раствора чистым растворителем.
Рис. 2. Зависимость парциальных и общего давлений пара идеальных (штриховая линия) и реальных (сплошная линия) бинарных растворов от состава при положительных (слева) и отрицательных (справа) отклонениях от закона Рауля.
Криоскопия – это метод физико-химического исследования, основанный на измерении понижения температуры замерзания раствора по сравнению с температурой замерзания чистого растворителя.
|
|
|
Для разбавленного идеального бинарного раствора понижение температуры замерзания пропорционально моляльности раствора и зависит от природы растворителя
DТ = Т0 – Т = K . m (IV)
где Т0 – температура замерзания растворителя,
Т - температура замерзания раствора,
m – моляльная концентрация раствора,
К – коэффициент пропорциональности.
Если m = 1, т.е. 1 моль вещества растворен в 1000 г растворителя, то DТ = К, поэтому постоянную К в уравнении (IV) называют моляльным понижением температуры замерзания раствора, или криоскопической постоянной. Она зависит только от природы растворителя и не зависит от концентрации раствора и химического состава растворенного вещества.
Для экспериментального определения К следует измерить понижение температуры замерзания в разбавленных растворах, а затем пересчитать эти данные на 1 моль:
, m = 1 моль/1000 г р-ля, 
(V)
Криоскопическую постоянную можно вычислить теоретически, зная температуру замерзания растворителя Т0, его молярные массу М0 НDи теплоту плавления пл., по уравнению:
(V a)
Криоскопические постоянные некоторых растворителей приведены в таблице:
|
|
|
Если из раствора при замерзании выпадают кристаллы чистого растворителя, то понижение температуры замерзания раствора используют для определения молярной массы растворенного вещества (М).
Если в q0 г растворителя растворено q г вещества, то моляльность полученного раствора (m) равна:
(VI)
Подставляя это выражение в формулу (1), получим:
,
откуда молярная масса растворенного вещества (М) равна:
(VII)
Массы q0 и q находят взвешиванием; К (для данного растворителя) – постоянная величина. Следовательно, опыт сводится Т,Dк определению т.е. к определению понижения температуры замерзания раствора, приготовленного из q0 г растворителя и q г растворенного вещества.
Криоскопический метод применим только к разбавленным ТDрастворам, вследствие чего для получаются очень небольшие значения. При выполнении этой работы пользуются термометрами, позволяющими делать отсчет с точностью.
Изотонический коэффициент показывает во сколько раз реальное число частиц растворенного вещества больше чем теоретически ожидаемое (если предполагать, что вещество в растворе присутствует только в виде молекул).
Для идеальных растворов электролитов i>1.
Коэффициент Вант-Гоффа показывает также во сколько раз наблюдаемое опытное значение росм.,Dtкип.,Dtзам., 
больше теоретически вычисленного, т.е.:
Дата добавления: 2018-04-04; просмотров: 1640; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!