Общая факторная и остаточная суммы
Квадратов отклонений
Пусть на количественный нормально распределенный признак X воздействует фактор F, который имеет р постоянных уровней. Будем предполагать, что число наблюдений (испытаний) на каждом уровне одинаково и равно q.
| Номер испытания | Уровни фактора Fj | |||
| F1 | F2 | … | Fp | |
| 1 2 … q | х11 х21 … хq1 | х12 х22 … хq2 | … … … … | х1p х2p … хqp |
| Групповая средняя | ||||
Пусть наблюдалось n = pq значений xij признака X, где i - номер испытания (i = 1,2, ..., q), j - номер уровня фактора (j = 1, 2, ..., р). Результаты наблюдений приведены в табл. 30.
Введем, по определению,
(общая сумма квадратов отклонений наблюдаемых значений от общей средней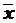 
),
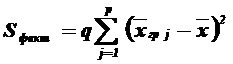
(факторная сумма квадратов отклонений групповых средних от общей средней, которая характеризует рассеяние «между группами»),
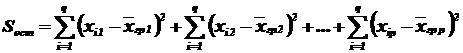
(остаточная сумма квадратов отклонений наблюдаемых значений группы от своей групповой средней, которая характеризует рассеяние «внутри групп»).
Практически остаточную сумму находят по равенству
Sост = Sобщ – Sфакт
Элементарными преобразованиями можно получить формулы, более удобные для расчетов:
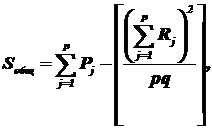
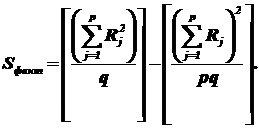
где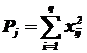 
- сумма квадратов значений признака на уровне Fj , 
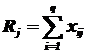- сумма значений признака на уровне Fj.
Общая, факторная и остаточная дисперсии
Разделив суммы квадратов отклонений на соответствующее число степеней свободы, получим общую, факторную и остаточную дисперсии:
|
|
|
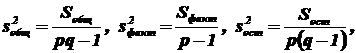
где р - число уровней фактора; q - число наблюдений на каждом уровне; pq - 1 -число степеней свободы общей дисперсии; р – 1 - число степеней свободы факторной дисперсии; p(q - 1) - число степеней свободы остаточной дисперсии.
Если нулевая гипотеза о равенстве средних справедлива, то все эти дисперсии являются несмещенными оценками генеральной дисперсии.
Сравнение нескольких средних методом дисперсионного анализа
Вернемся к задаче, поставленной выше: проверить при заданном уровне значимости нулевую гипотезу о равенстве нескольких (р > 2) средних нормальных совокупностей с неизвестными, но одинаковыми дисперсиями. Покажем, что решение этой задачи сводится к сравнению факторной и остаточной дисперсий по критерию Фишера — Снедекора.
1. Пусть нулевая гипотеза о равенстве нескольких средних (далее будем называть их групповыми) правильна. В этом случае факторная и остаточная дисперсии являются несмещенными оценками неизвестной генеральной дисперсии и, следовательно, различаются незначимо. Если сравнить эти оценки по критерию F, то очевидно, критерий укажет, что нулевую гипотезу о равенстве факторной и остаточной дисперсий следует принять.
Таким образом, если гипотеза о равенстве групповых средних правильна, то верна и гипотеза о равенстве факторной и остаточной дисперсий.
|
|
|
2. Пусть нулевая гипотеза о равенстве групповых средних ложна. В этом случае с возрастанием расхождения между групповыми средними увеличивается факторная дисперсия, а вместе с ней и отношение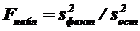 
. В итоге Fнабл окажется больше Fкр и, следовательно, гипотеза о равенстве дисперсий будет отвергнута.
Таким образом, если гипотеза о равенстве групповых средних ложна, то ложна и гипотеза о равенстве факторной и остаточной дисперсий.
Итак, для того чтобы проверить нулевую гипотезу о равенстве групповых средних нормальных совокупностей с одинаковыми дисперсиями, достаточно проверить по критерию F нулевую гипотезу о равенстве факторной и остаточной дисперсий. В этом и состоит метод дисперсионного анализа.
Замечание 1. Если факторная дисперсия окажется меньше остаточной, то уже отсюда следует справедливость гипотезы о равенстве групповых средних и, значит, нет надобности прибегать к критерию F.
Замечание 2. Если нет уверенности в справедливости предположения о равенстве дисперсий рассматриваемых р совокупностей, то это предположение следует проверить предварительно.
|
|
|
Дата добавления: 2018-04-04; просмотров: 565; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!