Доверительные интервалы для оценки математического ожидания
нормального распределения при известном s
Пусть количественный признак X генеральной совокупности распределен нормально, причем среднее квадратическое отклонение s этого распределения известно. Требуется оценить неизвестное математическое ожидание а по выборочной средней 
. Поставим своей задачей найти доверительный интервал, покрывающие параметр а с надежностью g. Можно показать, что искомый доверительный интервал имеет вид:
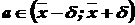, где 
.
Здесь t – квантиль нормированного нормального распределения, который находится как корень уравнения
.
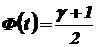Для вычисления t можно воспользоваться встроенной функцией табличного процессора MS Excel:
.
Из формулы можно сделать следующие выводы:
1) при возрастании объема выборки n число d убывает и, следовательно, точность оценки увеличивается;
2) увеличение надежности оценки g приводит к увеличению t (Ф (t) - возрастающая функция), следовательно, и к возрастанию d; другими словами, увеличение надежности классической оценки влечет за собой уменьшение ее точности.
Если требуется оценить математическое ожидание с наперед заданной точностью d и надежностью g, то минимальный объем выборки, который обеспечит эту точность, находят по формуле:
.
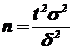Доверительные интервалы для оценки математического ожидания
нормального распределения при неизвестном s
Пусть количественный признак X генеральной совокупности распределен нормально, причем среднее квадратическое отклонение s неизвестно. Требуется оценить неизвестное математическое ожидание а с помощью доверительных интервалов. Разумеется, невозможно воспользоваться результатами предыдущего параграфа, в котором s предполагалось известным.
|
|
|
Можно показать, что доверительный интервал в этом случае имеет вид:
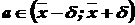, где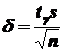 
.
Здесь tg – квантиль распределения Стьюдента, который находится как корень уравнения
.
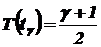Для вычисления tg можно воспользоваться встроенной функцией табличного процессора MS Excel:
.
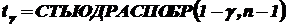При неограниченном возрастании объема выборки п распределение Стьюдента стремится к нормальному. Поэтому практически при n > 30 можно вместо распределения Стьюдента пользоваться нормальным распределением. Однако важно подчеркнуть, что для малых выборок (n < 30), в особенности для малых значений п, замена распределения нормальным приводит к грубым ошибкам, а именно к неоправданному сужению доверительного интервала, т. е. к повышению точности оценки. Например, если n = 5 и g = 0,99, то, пользуясь распределением Стьюдента, найдем tg= 4,6, а используя функцию Лапласа, найдем t = 2,58, т. е. доверительный интервал в последнем случае окажется более узким, чем найденный по распределению Стьюдента.
|
|
|
Дата добавления: 2018-04-04; просмотров: 364; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!