ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ
СЛУЧАЙНОЙ ВЕЛИЧИНЫ
Определение функции распределения
Рассмотрим непрерывную случайную величину (НСВ). Невозможно дать перечень всех ее возможных значений. С этой целью и вводят функции распределения вероятностей случайной величины.
Пусть х - действительное число. Вероятность события, состоящего в том, что X примет значение, меньшее х, т. е. вероятность события X < х, обозначим через F(х). Функцией распределения называют функцию F(х), определяющую вероятность того, что случайная величина X в результате испытания примет значение, меньшее х, т. е.
 .
.
Геометрически это равенство можно истолковать так: F(х) есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки х.
Свойства функции распределения
Свойство 1. Значения функции распределения принадлежат отрезку [0, 1]:
Свойство 2. F(х) - неубывающая функция, т. е. F(x2) > F(x1), если х2 > х1.
Следствие 1. Вероятность того, что случайная величина примет значение, заключенное в интервале (а, b), равна приращению функции распределения на этом интервале:
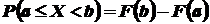 .
.
Следствие 2. Вероятность того, что непрерывная случайная величина X примет одно определенное значение, равна нулю.
Свойство 3. Если возможные значения случайной величины принадлежат интервалу (а, b), то: 1) F(x) = 0 при х ≤ а; 2) F(х) = 1 при х ³ b.
График функции распределения
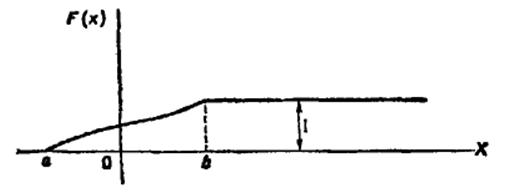
ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ
|
|
|
НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
Определение плотности распределения
Непрерывную случайную величину можно также задать, используя другую функцию, которую называют плотностью распределения вероятностей.
Плотностью распределения вероятностей непрерывной случайной величины X называют функцию f(х) - первую производную от функции распределения F(х):
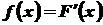 .
.
Из этого определения следует, что функция распределения является первообразной для плотности распределения. Заметим, что для описания распределения вероятностей дискретной случайной величины плотность распределения неприменима.
Вероятность попадания непрерывной
Случайной величины в заданный интервал
Зная плотность распределения, можно вычислить вероятность того, что непрерывная случайная величина примет значение, принадлежащее заданному интервалу.
Теорема. Вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу (а, b), равна определенному интегралу от плотности распределения, взятому в пределах от а до b:
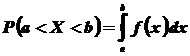
Геометрически полученный результат можно истолковать так: вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу (а, b), равна площади криволинейной трапеции, ограниченной осью Ох, кривой распределения f(х) и прямыми х = а и х = b.
|
|
|
Дата добавления: 2018-04-04; просмотров: 315; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
