Числовые характеристики дискретных случайных величин (ДСВ)
Как уже известно, закон распределения полностью характеризует случайную величину. Однако часто закон распределения неизвестен и приходится ограничиваться меньшими сведениями. Иногда даже выгоднее пользоваться числами, которые описывают случайную величину суммарно; такие числа называют числовыми характеристиками случайной величины. К числу важных числовых характеристик относится математическое ожидание.
Математическое ожидание, как будет показано далее, приближенно равно среднему значению случайной величины. Для решения многих задач достаточно знать математическое ожидание. Например, если известно, что математическое ожидание числа выбиваемых очков у первого стрелка больше, чем у второго, то первый стрелок в среднем выбивает больше очков, чем второй, и, следовательно, стреляет лучше второго. Хотя математическое ожидание дает о случайной величине значительно меньше сведений, чем закон ее распределения, но для решения задач, подобных приведенной и многих других, знание математического ожидания оказывается достаточным.
Математическое ожидание дискретной случайной величины
Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности:
Пусть случайная величина X может принимать только значения x1, x2, ..., хп, вероятности которых соответственно равны р1, р2, . . ., рп. Тогда математическое ожидание М(X) случайной величины X определяется равенством
|
|
|
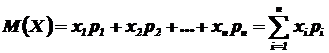 .
.
Замечание. Из определения следует, что математическое ожидание дискретной случайной величины есть неслучайная (постоянная) величина. Рекомендуем запомнить это утверждение, так как далее оно используется многократно.
Пример. Найти математическое ожидание числа появлений события А в одном испытании, если вероятность события А равна р.
Решение. Случайная величина X - число появлений события А в одном испытании - может принимать только два значения: х1 = 1 (событие А наступило) с вероятностью р и х2 = 0 (событие А не наступило) с вероятностью q= 1 - р. Искомое математическое ожидание:
M(X) = 1∙p+0∙(1 – p) = p /
Математическое ожидание приближенно равно (тем точнее, чем больше число испытаний) среднему арифметическому наблюдаемых значений случайной величины.
Свойства математического ожидания
Свойство 1. Математическое ожидание постоянной величины равно самой постоянной:
М(С) = С.
Свойство 2. Постоянный множитель можно выносить за знак математического ожидания:
М(СХ) = СМ(X).
Замечание. Прежде чем перейти к следующему свойству, укажем, что две случайные величины называют независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина. В противном случае случайные величины зависимы. Несколько случайных величин называют взаимно независимыми, если законы распределения любого числа из них не зависят от того, какие возможные значения приняли остальные величины.
|
|
|
Свойство 3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:
M(XY) = M(X)M(Y).
Свойство 4. Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых:
М(X + Y) = М(X) + М(Y).
Эти свойства распространяются на большее число сомножителей и слагаемых.
Пример. Найти математическое ожидание суммы числа очков, которые могут выпасть при бросании двух игральных костей.
Решение. Обозначим число очков, которое может выпасть на первой кости, через X и на второй - через Y. Возможные значения этих величин одинаковы и равны 1, 2, 3, 4, 5 и 6, причем вероятность каждого из этих значений равна 1/6. Найдем математическое ожидание числа очков, которые могут выпасть на первой кости:
 .
.
Очевидно, что и М (Y) = 7/2.
Искомое математическое ожидание
М(X + Y) = М(X) + М(Y) = 7/2 + 7/2 = 7.
|
|
|
Дата добавления: 2018-04-04; просмотров: 367; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
