Основные задачи, решаемые методом координат

Задача о расстоянии между двумя точками. Найдем расстояние d между двумя заданными точками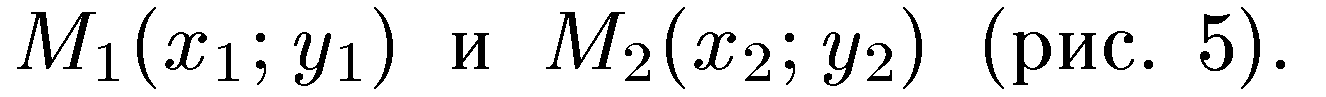

Из прямоугольного треугольника 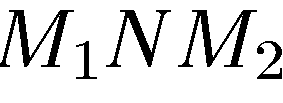по теореме Пифагора имеем:

Из курса геометрии девятилетней школы известно, что расстояние d между точками А и В, расположенными на координатной прямой (оси), вычисляется по формуле 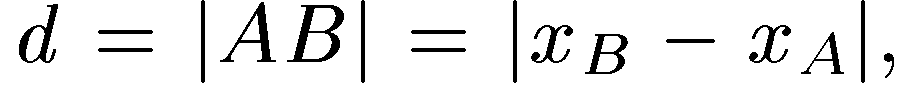где - координаты точек А и В этой прямой.

Тогда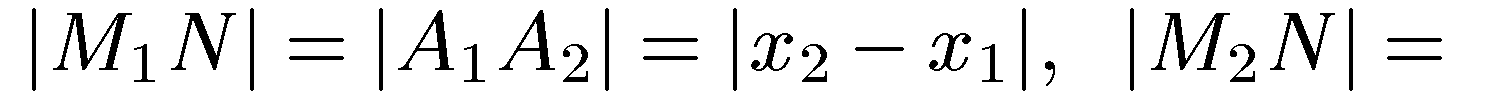

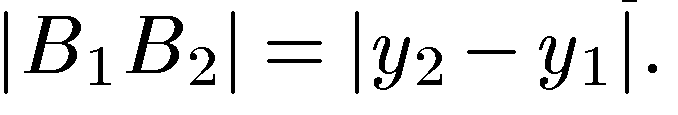
Поэтому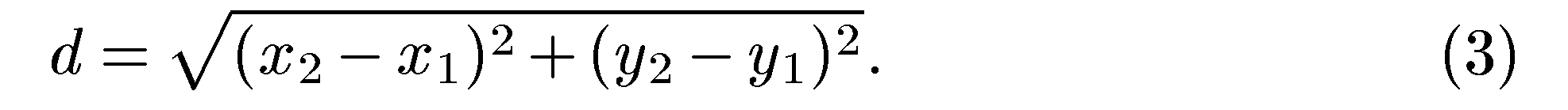

Пример. Найти расстояние между точками А(—1; —2) и В(—4; —2). По формуле (3) имеем:

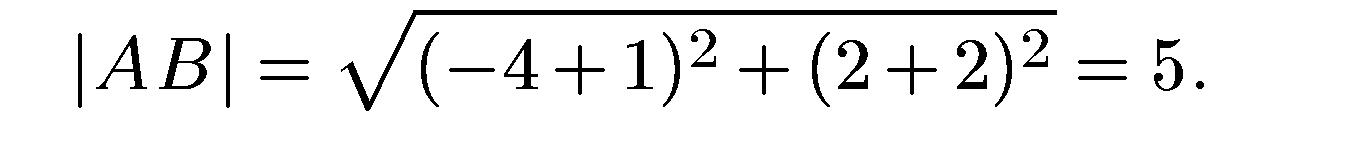
Задача о делении отрезка в данном отношении. Пусть даны точки Требуется найти точку , лежащую на отрезке и делящую его в данном отношении

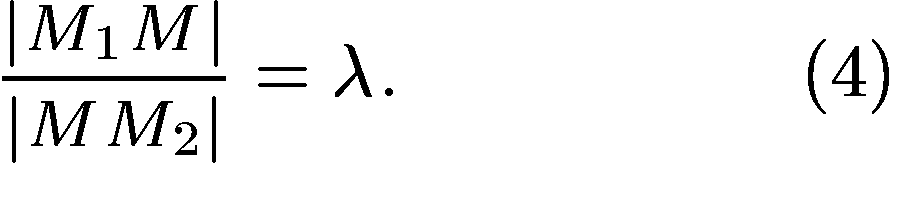
Опустим из точек перпендикуляры на ось Ох (рис. 6).

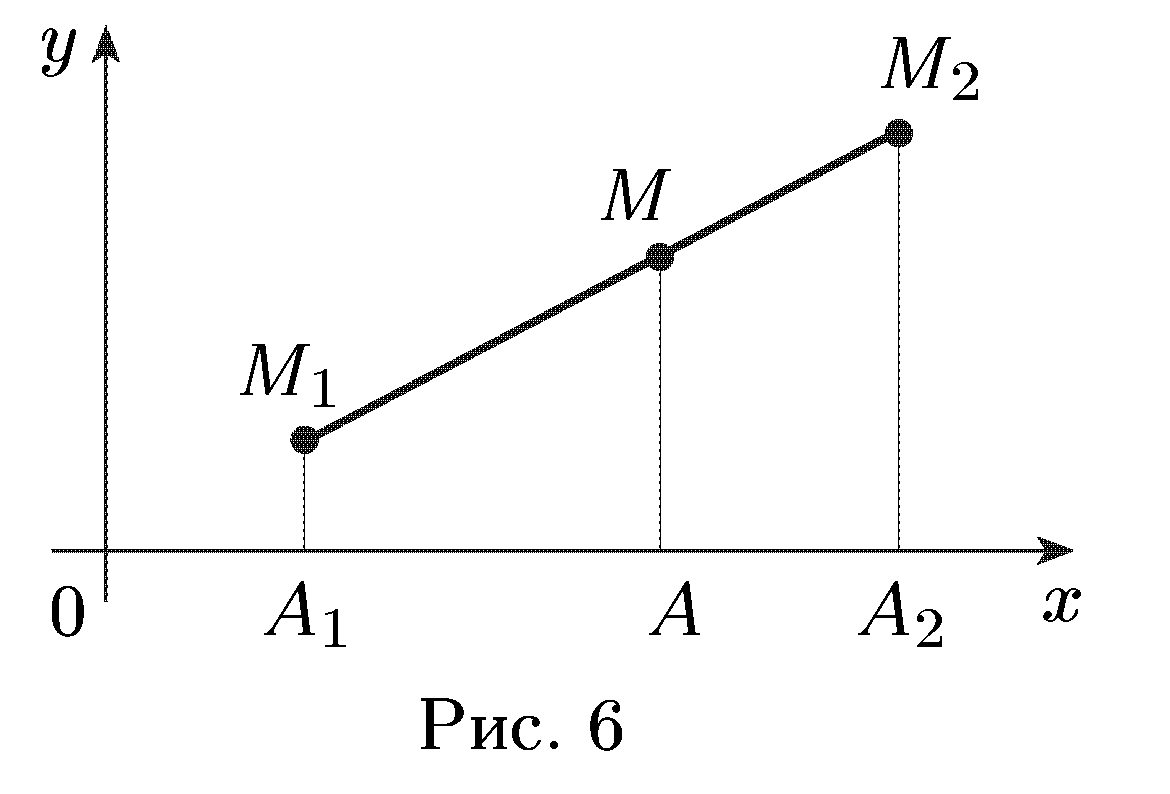
По известному предложению из элементарной геометрии о пересечении сторон угла параллельными прямыми получим:

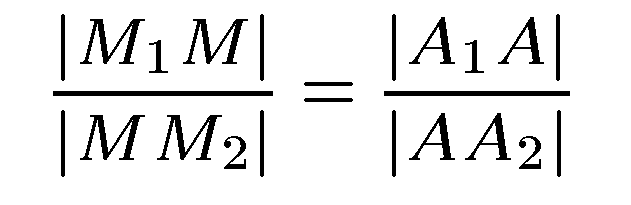
При выбранном расположении точек имеем:

Поэтому заданное отношение (2) принимает вид:

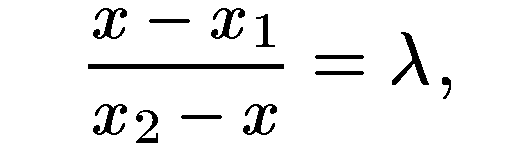
откуда:

Аналогично

В частности, если λ = 1, т. е. при делении отрезка 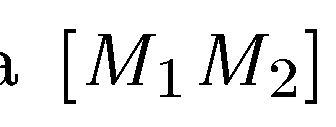пополам,

получаем: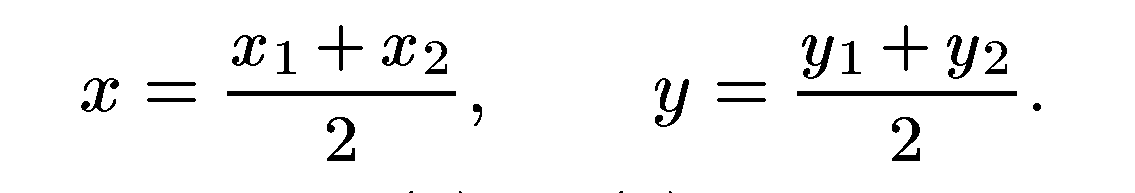

Примечание. Формулы (5) и (6) верны при любом расположении точек .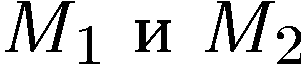

Пример. Вычислить координаты точки М(x; у), делящей отрезок 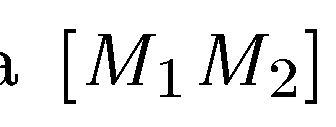между точками 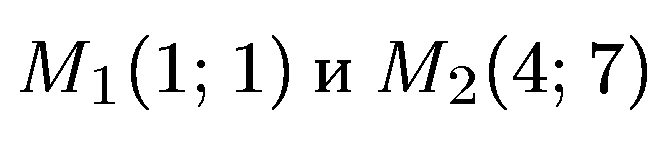в отношении 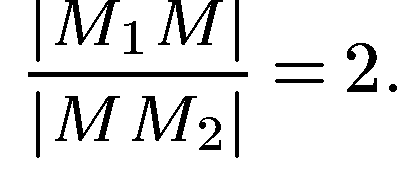Согласно формулам (5) и (6) имеем:

4. Уравнение линии на плоскости. Прямоугольная и полярная системы координат позволяют задавать различные линии на плоскости их уравнениями.

Определение. Уравнением линии на плоскости в прямоугольной системе координат называется уравнение

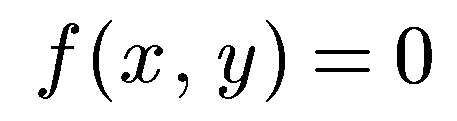с переменными х и у, которому удовлетворяют координаты каждой точки данной линии и не удовлетворяют координаты любой точки плоскости, не лежащей на этой линии.

Переменные х и у уравнения линии называются текущими координатами.

Покажем, например, что уравнениех — у = 0 или

х = у (7)

является уравнением биссектрисы 1-го и 3-го координатных углов.

По свойству биссектрисы угла для произвольной точки М(х; у)

(лежащей на биссектрисе) имеем: или

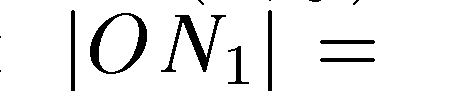
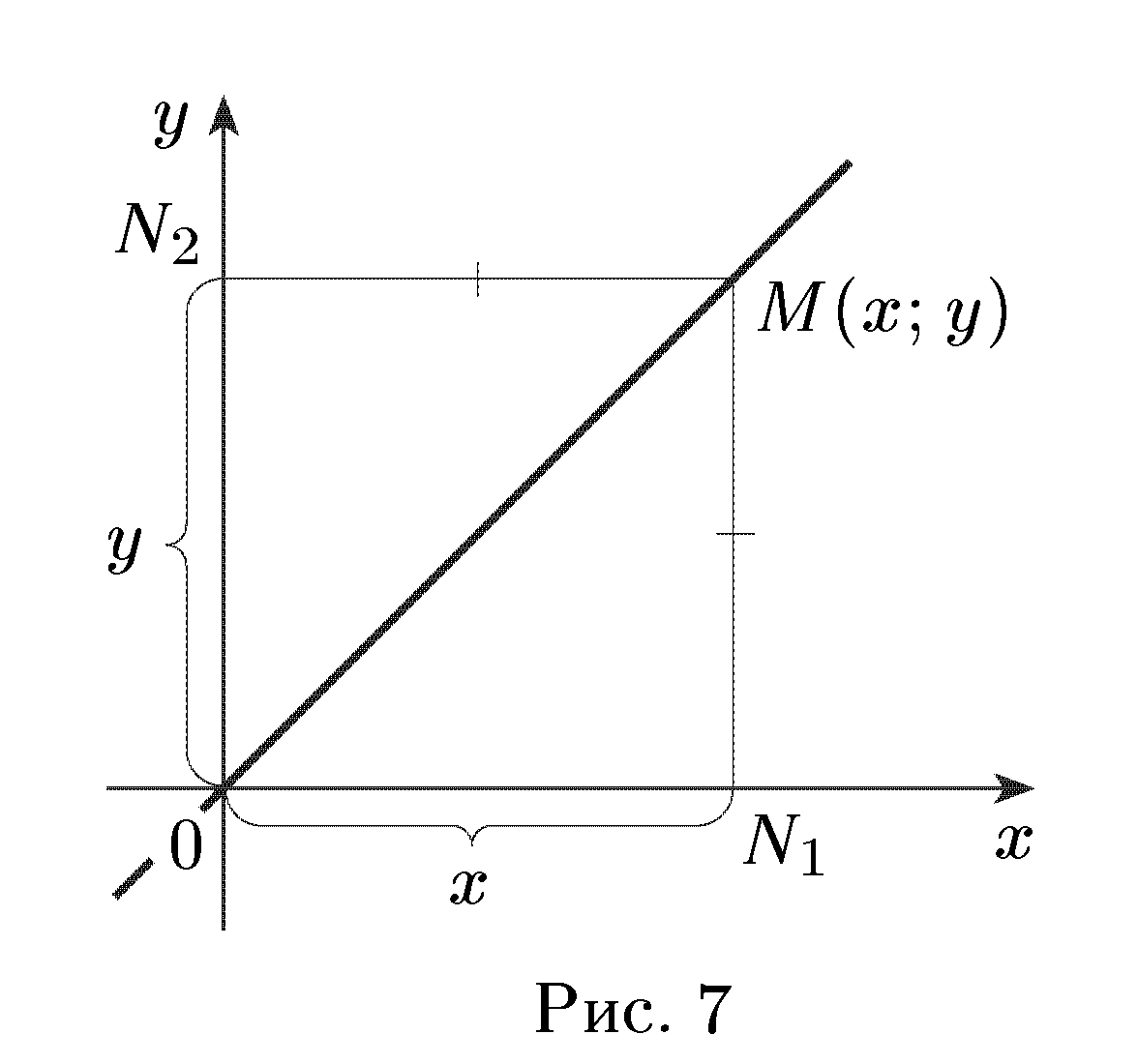
и поэтому х = у, т. е. координаты всех точек биссектрисы удовлетворяют уравнению (7). Очевидно также, что у любой точки, не лежащей на данной биссектрисе, координаты не равны между собой и не удовлетворяют уравнению (7).

Отметим, что геометрическим образом данного заранее уравнения не

всегда является линия. Может случиться, что уравнению соответствует лишь несколько точек (уравнению 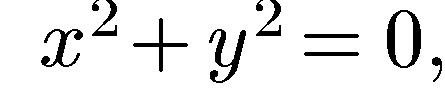например, на плоскости соответствует только одна точка (0; 0)). Встречаются и такие случаи, когда заданному уравнению не соответствует на плоскости ни одной точки (например, уравнению ).

Прямая линия

1. Уравнение прямой с угловым коэффициентом. Пусть прямая ℓ не параллельна оси Оу (рис. 8). Обозначим точку пересечения ℓ с осью Оу через B(0;b), а угол между положительным направлением оси Ох и ℓ через отсчитываемый от Ох против часовой стрелки 0≤φ<π, называется углом наклона прямой ℓ к оси Ох.

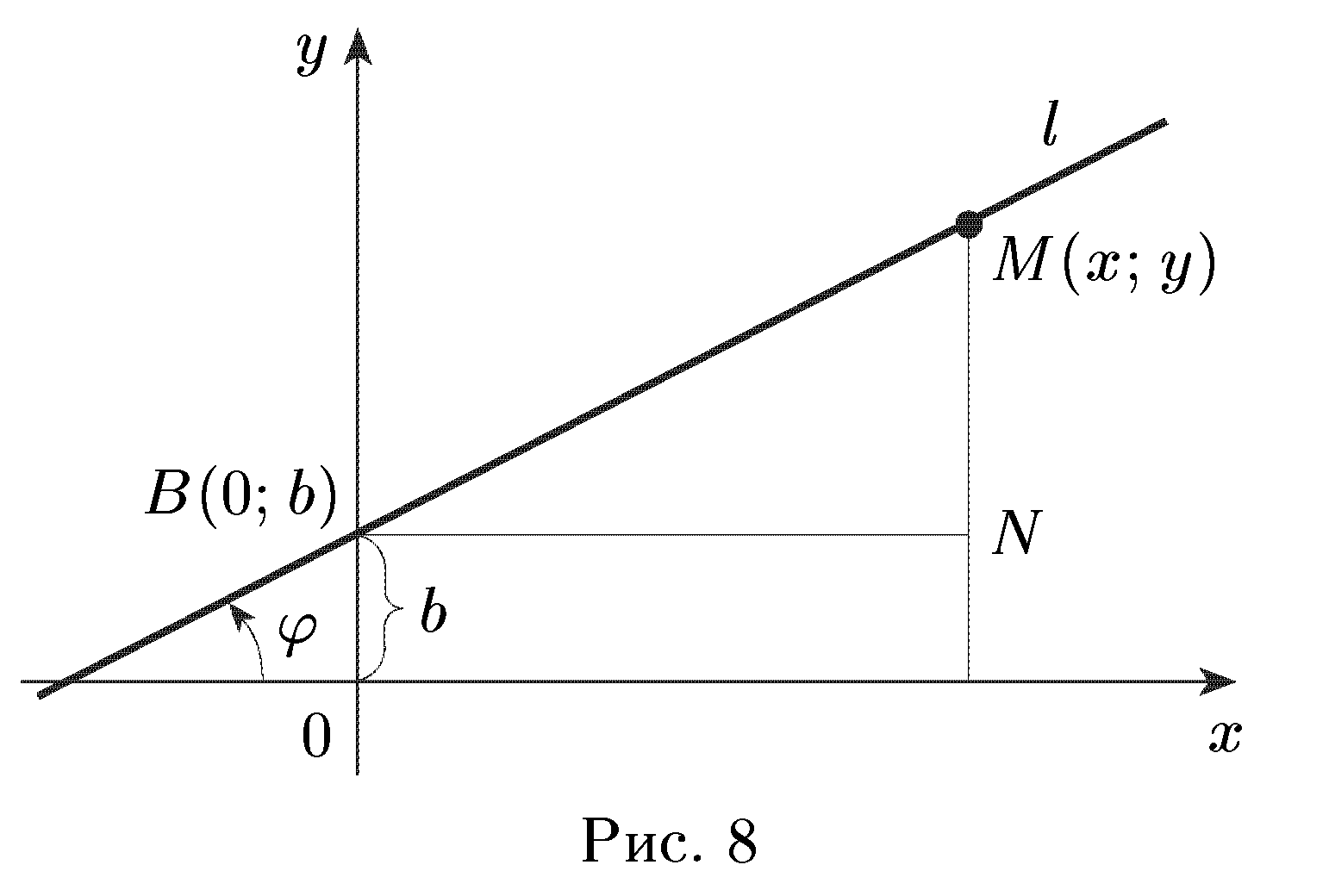
Выведем уравнение прямой ℓ.

Пусть М(х; у) — произвольная точка прямой ℓ с текущими координатами х и у. Из прямоугольного треугольника BNM (рис. 8) имеем:

Эту величину называют угловым коэффициентом прямой и обозначают через к: к = tgφ. Тогда из (1) получим:

откуда:

у = kх + b (2)

Уравнение (2) называется уравнением прямой с угловым коэффициентом; число b называется начальной ординатой (это ордината точки В).

Пример. Если и уравнение данной

прямой имеет вид у = x — 3.

Если в уравнении (2) k = 0, то имеем уравнение

y = b, (3)

прямой параллельной оси Ох и проходящей через точку В(0;b). При b = 0 из (3) получаем уравнение координатной оси Ох: у = 0.

По аналогии с уравнением (3) уравнение

х = а (4)

есть уравнение прямой, параллельной оси Оу и проходящей через точку A(а;0). При а = 0 из (4) имеем уравнение координатной оси Оу: х = 0.

2. Общее уравнение прямой. Уравнением с угловым коэффициентом может быть задана любая прямая на плоскости, не параллельная оси ординат. При рассмотрении уравнения первой степени

Ах + Ву + С = 0, (5)

в котором коэффициенты А и В одновременно не равны нулю, оказывается, что любую прямую без каких-либо ограничений, можно задать уравнением (5).

Теорема. Каждая прямая на плоскости с прямоугольной декартовой системой координат определяется уравнением первой степени, и наоборот: каждое уравнение первой степени определяет некоторую прямую на плоскости.

Доказательство. 1) Пусть дана прямая, не параллельная оси ординат. В этом случае прямая описывается уравнением с угловым коэффициентом

у = kх + b, которое является частным случаем уравнения (5) при А = k, В =1, С =b.

Пусть теперь прямая параллельна оси Оу. Тогда ее уравнение запишется в виде х = а. Это уравнение тоже частный случай уравнения (5) при А = 1, В = 0, С = —а. Итак, любая прямая на плоскости определяется уравнением первой степени.

2) Покажем теперь, что произвольному уравнению первой степени (5) (А и В одновременно не равны нулю) соответствует некоторая прямая на плоскости.

Действительно, если В ≠ 0, то уравнение (5) можно преобразовать в уравнение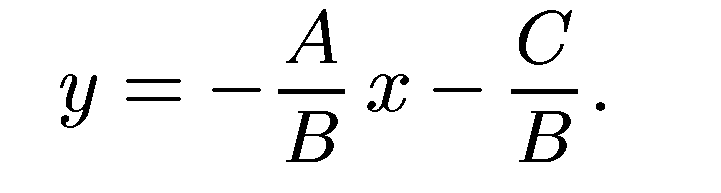

т. е. в уравнение прямой с угловым коэффициентом и начальной ординатой 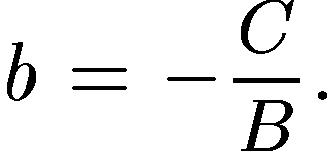Если В = О, А ≠ 0, то уравнение (5) преобразуется к виду 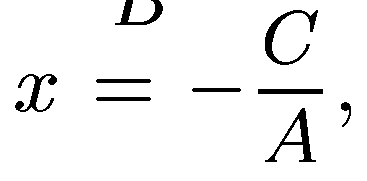т. е. в уравнение прямой, параллельной оси Оу. Теорема доказана.

Уравнение первой степени (5) (А и В одновременно не равны нулю), описывающее на плоскости любую прямую, называется общим уравнением прямой.

3. Уравнение прямой с данным угловым коэффициентом и проходящей через данную точку. Выведем уравнение прямой, проходящей через данную точку 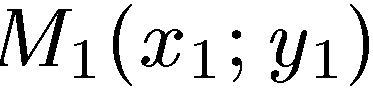и имеющей данный угловой коэффициент k. Уравнение этой прямой имеет вид:

у = kх + b. (6)

Так как искомая прямая проходит через точку , то

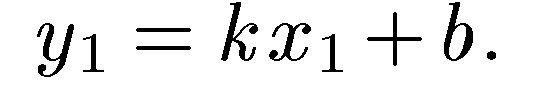(7)

Вычитая из равенства (6) равенство (7), получаем:

Это и есть уравнение искомой прямой.

Пример. Уравнение прямой, проходящей через точку М(—1;8), с угловым коэффициентом k= 1 согласно (8) есть у — 8 = х + 1, или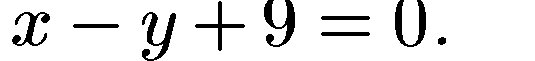

4. Уравнение прямой в отрезках. Предположим, что в общем уравнении прямой A≠0, B≠0 и C≠0. Перенеся в нем С в правую часть и разделив обе части полученного уравнения на —С, получим:

или

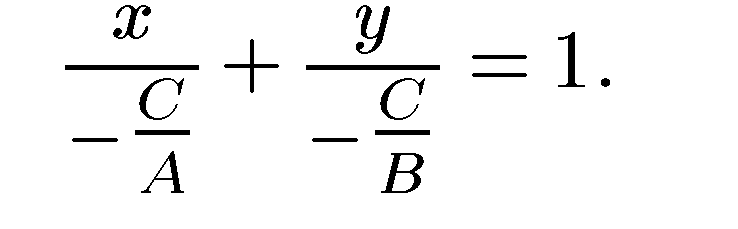
Отсюда, вводя обозначения 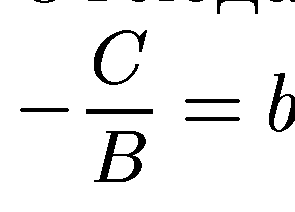, приходим к уравнению

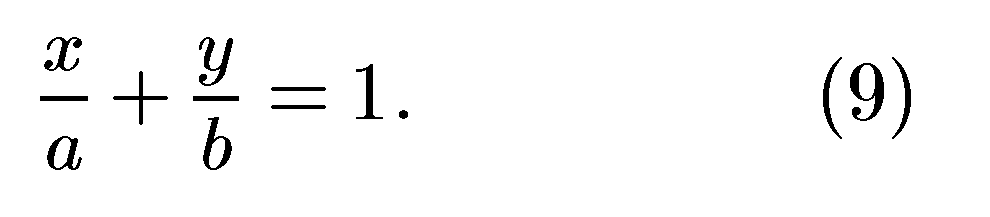
Уравнение (9) называется уравнением прямой в отрезках. Это название объясняется тем, что числа а и b определяются отрезками [ОА] и [OB], которые прямая отсекает на осях координат (рис. 9).

Такой вид уравнения удобен для построения прямой.

Заметим, что прямые, параллельные координатным осям, и прямые, проходящие через начало координат, не могут быть записаны уравнениями в отрезках.

Пример.Записать уравнение прямой 2х + 5у — 10 = 0 в отрезках и построить эту прямую. Перепишем данное уравнение в виде 2х + 5у = 10, откуда 1 и, значит, а = 5, b = 2. Наконец, откладываем на осях координат отрезки а = 5, 6 = 2 и через их концы (5; 0) и (0; 2) проводим прямую.

Задания:

1. Найти расстояние между точками:

а) A(-3;9) и B(3;1);

б) A(2;-1) и B(5; 3).

2. Вычислить площадь квадрата, две смежные вершины которого А(3;-7) и B(-1;4).

3. Даны две противоположные вершины квадрата A(3; 5) и C(1; —3). Вычислить площадь квадрата.

4. Найти координаты точки С, делящей отрезок [АВ] между точками А(—2; 1) и В(8; 6) в отношении 3 : 2, считая от точки А.

5. Даны вершины треугольника А(—7; 4), В(—5; 2) и C(6; —3). Найти

координаты середин всех сторон треугольника.

6. Найти полярные координаты точек М(2; 2), N( 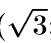; 1).

7. Найти прямоугольные координаты точек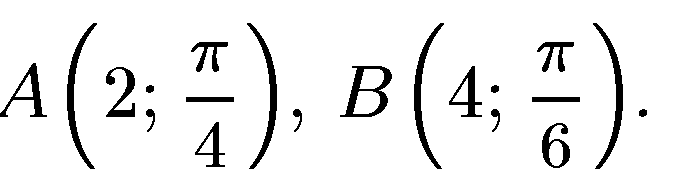

8. Определить, какие из точек A(2; 3), B(3; 3) и C(4; 4) лежат на прямой

9. Записать уравнение прямой, проходящей через точку М(0; b) и име-

ющей угловой коэффициент k:

а) М(0;-2), k = 1;

б) М(0;0), k = -3;

в) М(0; 1), k = 0;

г) М(0;0), k = 0.

10. Найти координаты точки С, делящей отрезок [А В] между точкамиA(1; 2) и B(—1; 4) в отношении 1 : 2, считая от точки А.

11. Отрезок [AВ] разделен точкой C(4; 1) в отношении ,считая от

точки А. Найти:

а)координаты точки А;

б) длину отрезка [AВ], еслиизвестна точка В(8; 5).

12. Три последовательные вершины параллелограмма имеют координаты A(3; -3), B(-1; 1), С(1; 6). Найти:

а) координаты четвертой вершины D;

б) длину отрезка [ВD].

13. Найти координаты точки C— середины отрезка [AВ], если:

а) A(5;-4) и B(-1; 2);

б) A(6;-3) и B(-2;-7).

14. Построить точки по их полярным координатам: A(6; 0), ,

15. Записать уравнение прямой, проходящей через точку и имеющей угловой коэффициент k:

а) М(1;2), k = l;

б)

в)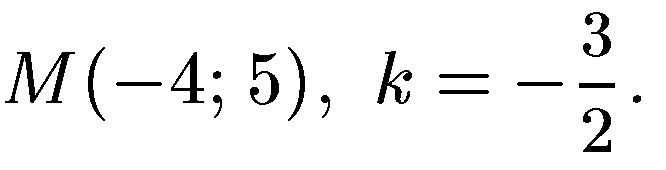

16. Прямая проходит через точки А и В:

а) A(0;3), В(4;0);

б) A(-2; 0), В(0;-5).

Написать уравнение прямой в отрезках.

17. Найти угол φ, образованный прямыми у = 3x + 5 и y = —2x + 7.

18. Найти угол φ,образованный прямым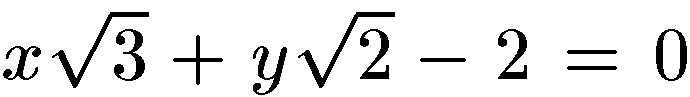и и

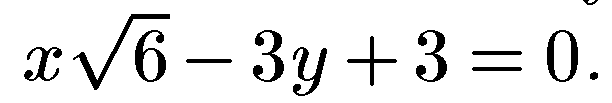
19. Написать уравнение прямой, проходящей через точку А(—2; 6) и параллельной прямой 5x +3y — 7 = 0.

20. Написать уравнение прямой, проходящей через точку А(—1; 1) и перпендикулярной прямой 3x — y — 2 = 0.

21. Параллельны ли прямые 3x — 6y + 4 = 0 и 5x— 10y — 1 = 0?

22. Найти точку пересечения двух прямых:

а) x+y—7=0 иx—7y+1=0

б) 2x+ 3y—12 = 0 и х—у—1 = 0.

23. Определить координаты вершин треугольника, если даны уравнения его сторон: у = 2х — 1, 2у — x = 3, 3y + 2x — 5 = 0.

24. Найти расстояние от точки А(2; 5) до прямой 6x + 8y — 5 = 0.

25. Найти расстояние от точки А(—3; 4) до прямой 12x + 5у — 10 = 0.

26. Написать уравнение окружности с центром в точке 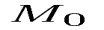и радиусом R, если даны:

а) 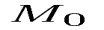(—1;2) и R=5;

б) 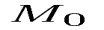(—2;—3) и R= ;

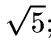в) (0;5) и R=6;

27. Написать каноническое уравнение эллипса, если даны его полуоси а = 5, b = 4.

28. Дан эллипс 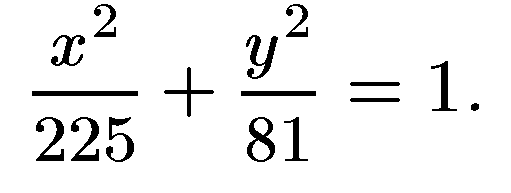. Определить его оси и расстояние между фокусами.

29. Дан эллипс 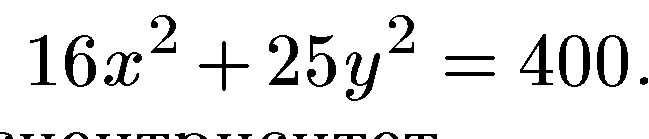. Найти длины осей, координаты вершин и фокусов и эксцентриситет.

30. Написать каноническое уравнение гиперболы, если даны:

а) а = 7, b = 2;

б) а = 4, с = 5;

в) b= 9, с =15.

31. Дана гипербола 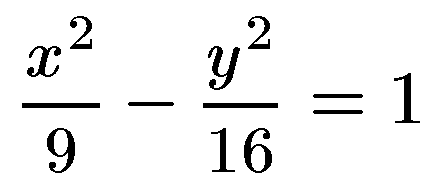.Определить расстояние между фокусами.

32. Дана гипербола 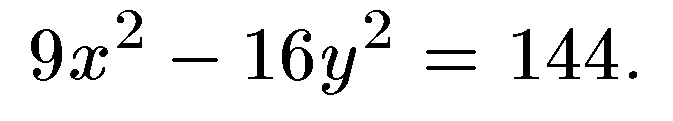. Определить расстояние между фокусами и эксцентриситет.

33. Написать уравнения двух парабол с вершиной в начале координат, зная, что координаты их фокусов равны:

a) F(4;0);

б) F(—2;0).

34. Определить координаты фокусов следующих парабол:

а) ;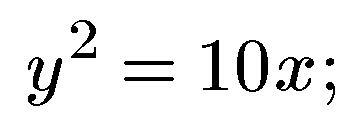

б)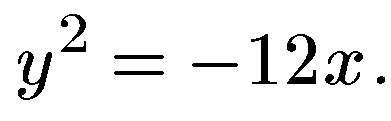

35. Дана парабола 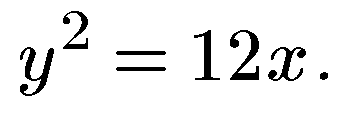. Написать уравнение директрисы.

36. Написать уравнения парабол с вершиной в начале координат, для которых директрисами служат прямые:

а) x = —2;

б) x = 3.

37. Вычислить площадь треугольника с вершинами:

а) A(0;3), B(2;2), С(3; 0);

б) A(2;3), B(4;—1), С(6; 5).

Дата добавления: 2018-02-28; просмотров: 1477; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 34

Мы поможем в написании ваших работ!