Основные понятия о множествах
1.1. Основные определения.
Одним из основных понятий математики является понятие множества, и, как каждое основное понятие, не поддаётся точному определению (например, понятия “точка”, “прямая” являются одними из основных понятий геометрии).
МНОЖЕСТВОМ называется собрание, совокупность объектов, объединенных по какому-нибудь общему признаку, свойству.
Примеры:
1. Множество студентов данной учебной группы.
2. Множество планет солнечной системы.
3. Множество букв русского алфавита.
4. Множество натуральных чисел.
Математический смысл слова “множество” отличается от того, как оно используется в обычной речи. Так, в обычной речи понятие “множество” связывают с большим числом предметов, в математике же этого не требуется. Здесь могут рассматриваться множества, содержащие один объект, много объектов, несколько объектов или не содержащие ни одного объекта.
Объекты, из которых состоит множество, называются его ЭЛЕМЕНТАМИ.
Остановимся на символике, обычно использующейся при обращении с множествами.
Множества обозначаются прописными (заглавными) буквами латинского алфавита (без индексов или с индексами). Например: B, C,…,X,Y,…,A1,B1,…
Элементы множества обозначаются строчными (малыми) буквами латинского алфавита. Например: b,c,…,x,y,…,a1,b1,…
В математике особую роль играют множества, элементами которых являются числа. Такие множества называются ЧИСЛОВЫМИ. Некоторые числовые множества имеют специальные обозначения, вводимые для удобства пользования. Один из вариантов этих обозначений, которыми мы будем пользоваться в дальнейшем, выглядит следующим образом:
|
|
|
N – множество всех натуральных чисел;
Zc(или Z+ или C+) – множество всех целых неотрицательных чисел;
Z (или C) – множество всех целых чисел;
Q – множество всех рациональных чисел;
R – множество всех действительных чисел;
R+ - множество всех действительных положительных чисел.
По числу элементов, входящих в множество, множества делятся на три класса:
1 – конечные, 2 – бесконечные, 3 – пустые.
1. Если элементы множества можно сосчитать, то множество является КОНЕЧНЫМ.
Пример 1.
Множество гласных букв в слове “математика” состоит из трёх элементов – это буквы “а”, “е”, “и”, причем, гласная считается только один раз, т.е. элементы множества при перечислении не повторяются.
2. Если элементы множества сосчитать невозможно, то множество БЕСКОНЕЧНОЕ.
Пример 2.
Множество натуральных чисел бесконечно.
Пример 3.
Множество точек отрезка [0;1] бесконечно.
3. Множество, не содержащее ни одного элемента, называется ПУСТЫМ. Символически оно обозначается знаком Æ.
|
|
|
Пример 4.
Множество действительных корней уравнения x2 +1=0.
Пример 5.
Множество людей, проживающих на Солнце.
В математике часто приходится определять принадлежность данного элемента конкретному множеству.
Пример 6.
Мы говорим, что число 5 натуральное, т.е. утверждаем, что число 5 принадлежит множеству натуральных чисел. Символически принадлежность множеству записывается с помощью знака Î. В данном случае символическая запись будет такой: 5 ÎN. Читается: “5 принадлежит множеству натуральных чисел”.
Число 5,2 не принадлежит множеству натуральных чисел, т.к. не является натуральным числом. Символически отношение “не принадлежит” записывается с помощью знака 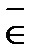 (реже Ï). Таким образом, здесь имеем: 5,2 ÏN
(реже Ï). Таким образом, здесь имеем: 5,2 ÏN
Читается: “5,2 не принадлежит множеству натуральных чисел”.
Способы задания множеств.
Множество считается заданным, если мы владеем способом, позволяющим для любого данного элемента определить, принадлежит он данному множеству или не принадлежит.
Множество можно задать, непосредственно перечислив все его элементы, причём, порядок следования элементов может быть произвольным. В этом случае названия всех элементов множества записываются в строчку, отделяются точкой с запятой и заключаются в фигурные скобки.
|
|
|
Пример 7.
Множество всех гласных букв русского алфавита:
A={а; я; у; ю; э; е;о; ё; и; ы}.
Пример 8.
Множество цифр десятичной системы счисления:
B={1; 2; 3; 4; 5; 6; 7; 8; 9; 0}.
Очевидно, что такой способ задания множеств удобно применять для конечных множеств с небольшим количеством элементов.
Конечные и бесконечные множества могут быть заданы другим способом: указанием ХАРАКТЕРИСТИЧЕСКОГО СВОЙСТВА, т.е. такого свойства, которым обладает любой элемент данного множества и не обладает ни один элемент, не принадлежащий ему.
Пусть P обозначает некоторое свойство, которым обладают все элементы множества А и не обладают элементы никакого другого множества. Тогда множество всех элементов, обладающих свойством Р, обозначим так:
А={х│х обладает свойством Р}={ х│Р(х)}={х : Р(х)}.
Свойство Р, задающее множество А, есть характеристическое свойство множества А.
Пример 9.
Множество чётных натуральных чисел. Зададим его с помощью характеристического свойства:
В={х │х – чётное натуральное число}={х │ х=2k, k Є N}.
Пример 10.
Множество всех действительных чисел на отрезке от 1 до 3 включительно запишется следующим образом:
|
|
|
R1-3={y│1≤ y≤ 3, y Є R}.
Следует заметить, что в ряде случаев одно и то же множество может быть задано как первым, так и вторым способом.
Пример 11.
Множество натуральных чисел, меньших, чем 10.
Первый способ: N<10={1; 2; 3; 4; 5; 6; 7; 8; 9}.
Второй способ: N<10={z│z<10, z Є N}.
Случается, что одно и то же множество может быть задано с помощью различных характеристических свойств.
Пример 12.
Множество квадратов.
Первый способ: A={x│x – ромб с прямыми углами}.
Второй способ: A={ x│x – прямоугольник с равными сторонами}.
Отношения между множествами.
Наглядно отношения между множествами изображают при помощи особых чертежей, называемых КРУГАМИ ЭЙЛЕРА (или диаграммами Эйлера – Венна).
Для этого множества, сколько бы они ни содержали элементов, представляют в виде кругов или любых других замкнутых кривых (фигур) – рис.1.
Рис. 1.
1. Пусть даны два множества: X={a; b; c; d} иY={l; k; m; b; c}. Множества Х и Y содержат некоторые одинаковые элементы, а именно “b” и “c” . В данном случае говорят, что множества X иY находятся в отношении ПЕРЕСЕЧЕНИЯ. С помощью кругов Эйлера данное отношение можно представить в виде рис. 2.
X Y B1 B2
Рис. 2. Рис. 3.
2. Пусть даны множества B1={1; 2; 3} и B2={4; 5; 6}.
Данные множества различны, у них нет одинаковых элементов. В таком случае говорят, что множества B1 и B2 находятся в отношении НЕПЕРЕСЕЧЕНИЯ.
С помощью кругов Эйлера данное отношение показано на рис. 3.
3. Пусть даны множества A={a; b; c; d; e} и B={a; b; c}.
Очевидно, что эти множества пересекаются; кроме того, каждый элемент
множества В является в то же время (одновременно) и элементом множества А. Тогда говорят, что множество В ВКЛЮЧЕНО в множество А, или что В есть ПОДМНОЖЕСТВО множества А.
Определение 1.1
| рис.4 |
| В |
| А |
Отношение “включено” обозначается знаком Ì.
Соответственно отношение “включает” – знаком É.
Определение 1.1 символически записывается так: ВÌА или АÉВ. С помощью кругов Эйлера данное отношение между множествами показано на рис.4.
Из определения подмножества следует, что всякое непустое множество А содержит по крайней мере два
множества: Ø и А, которые называются НЕСОБСТВЕННЫМИ
ПОДМНОЖЕСТВАМИ МНОЖЕСТВА. Все остальные подмножества (если они существуют) называются СОБСТВЕННЫМИ ПОДМНОЖЕСТВАМИ МНОЖЕСТВА. То есть, если В – собственное подмножество множества А, то имеем: ØÌ ВÌА, или иначе: АÉВÉ Ø.
4. Пусть даны множества C={x; y; z}, D={x; y; z}, которые состоят из одних и тех же элементов. В таком случае говорят, что множества С и D равны и пишут C=D.
Определение 1.2
Множества С и D называются равными, если они состоят из одних и тех же элементов.
Используя понятие “включено”, можно дать другое определение равенства множеств.
Определение 1.3
Множества C и D называются равными тогда и только тогда, когда множество С является подмножеством множества D, и наоборот.
Символически данное определение можно записать так:
С = DÛ С ÌD и DÌ С, или С = DÛ С ÌDÙDÌ С,
где знак Û означает “эквивалентность” (равнозначность), а знак Ù (конъюнкция) означает одновременность (совместность) осуществления тех операций (или событий), которые он соединяет.
С помощью кругов Эйлера отношение “равенство” показано на рис.5.
| u |
Рис.5. рис.6.
Универсальное множество.
Пусть U (или T – total) – некоторое фиксированное множество. Рассмотрим только такие множества А, В, С,…, которые являются подмножествами множества U. В этом случае множество U называется универсальным множеством всех множеств А, В, С,…
Примером универсального множества может служить множество действительных чисел, множество людей на планете Земля…
Мы его будем изображать прямоугольником с буквой U в правом верхнем углу (рис.6), внутри которого будут размещаться те или иные множества.
Операции над множествами.
Рассмотрим некоторые операции над множествами.
Пересечение множеств.
Пусть даны два множества: А={a; b; c; d} иB={c; d; e}.образуем новое множество Р, состоящее из всех элементов, принадлежащих одновременно и множеству А, и множеству В, т.е. Р={c;d}. Тогда говорят, что множество Р является пересечением множеств А и В.
Определение 1.4
Пересечением множеств А и В называется множество, состоящее их всех тех и только тех элементов, которые принадлежат множествам А и В одновременно.
Символически пересечение множеств А и В обозначается так: АÇВ, где символ Ç - знак пересечения множеств. Используя характеристическое свойство, определение 1.4 можно записать следующим образом:
Р=АÇВ= {x ïxÎA и xÎB}={xïxÎAÙxÎB}. (1)
Таким образом, (1) есть характеристическое свойство пересечения двух множеств.
Союз “и” иногда заменяют фигурной скобкой, и тогда (1) будет иметь вид:
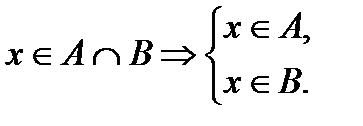 (2)
(2)
Для обозначения одновременной принадлежности множеству А и множеству В используется также знак Ù (конъюнкция, или логическое “и”):
xÎAÇBÞxÎAÙxÎB (2а)
Читаются выражения (2) и (2а) одинаково: если х принадлежит пересечению множеств А и В, то х принадлежит как множеству А, так и множеству В.
Если мы имеем ситуацию, когда х не принадлежит пересечению множеств А и В, то это означает, что х не принадлежит или множеству А, или множеству В.
Символически это может быть записано так:
 (3)
(3)
где квадратная скобка заменяет союз “или”.
В символической записи союз “или” может быть заменен также знаком Ú (дизъюнкция, логическое “или”):
хÏАÇВ Þ хÏА Ú хÏВ. (3а)
Читаются выражения (3) и (3а) одинаково: если х не принадлежит пересечению множеств А и В, то х не принадлежит или множеству А, или множеству В.
Графическая иллюстрация вариантов пересечения двух множеств приведена на рис. 7¸10 (пересечение заштриховано).
| А |
| Р |
| В |
| U |
| А |
| U |
| Р=B |
| U |
| Р=A=B |
| А |
| Р=Æ |
| В |
| U |
рис. 7 рис. 8 рис. 9 рис. 10
Объединение множеств.
Множества А и В входят в их объединение только один раз. Это вполне соответствует толкованию множества, принятому в математике: ни один элемент не может содержаться в множестве несколько раз.
Определение 1.5
Объединением двух множеств А и В называется такое множество С, которое состоит из всех тех элементов, которые принадлежат хотя бы одному из множеств А или В.
Символически объединение двух множеств А и В обозначается так:
А È В, где È - символ объединения множеств. Определение 1.5 можно записать с помощью характеристического свойства:
С= А È В={xïxÎA или xÎB}. (4)
Союз “или” иногда заменяют квадратной скобкой
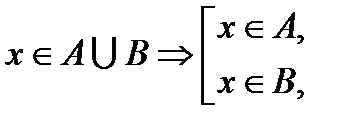 (5)
(5)
а также знаком дизъюнкции
х ÎА È В Þ хÎА Ú хÎВ. (5а)
Читаются эти знаки одинаково: если элемент х принадлежит объединению двух множеств А и В, то он принадлежит множеству А или множеству В.
Если же элемент х не принадлежит объединению множеств А и В, то он не принадлежит ни множеству А, ни множеству В. Символически это может быть записано так:
 (6)
(6)
или
x ÏAÈB Þ xÏA Ù xÏB. (6а)
Графически варианты объединения двух множеств показаны на рис. 11÷14 (объединение заштриховано).
| А |
| U |
| B |
| А |
| В |
| U |
| А |
| В |
| U |
| U |
| С=A=B |
рис. 11 рис. 12 рис. 13 рис. 14
Отметим некоторые очевидные свойства операции объединения двух множеств:
АÈА=А, АÈÆ=А, АÈU=U. (7)
Замечание1.
Если А1, А2,…, Аn – несколько множеств, то аналогично тому, как это делалось для двух множеств, определяется их пересечение, т.е. составляется множество, представляющее их общую часть:
Р= А1Ç А2Ç…Ç Аn={xïxÎ"Ai, i= 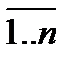 },
},
Где символ " (квантор всеобщности) заменяет слово “все”, и, таким образом, мы символически обозначили ту часть множеств Ai, которая принадлежит каждому множеству одновременно.
Замечание 2.
Если А1, А2,…, Аn – несколько множеств, то аналогично тому, как это делалось для двух множеств, определяется их объединение – составляется множество, состоящее из элементов, которые принадлежат хотя бы одному их них:
C= A1ÈA2È…ÈAn={x ï xÎA1 или xÎA2 или …или xÎAn}.
Замечание 3.
Если в выражении есть знаки È и Ç и нет скобок, то сначала выполняется операция пересечения, а потом – операция объединения (аналог сложению и умножению в арифметике).
Разность множеств.
Определение 1.6
Разностью двух множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат множеству А и не принадлежат множеству В.
Символически разность двух множеств обозначается так:
А ÷ В, где символ ÷ является знаком разности для множеств. С помощью характеристического свойства запишем определение 1.6 следующим образом:
C=A÷B={xïxÎAиxÏB} (8)
Или 
 (9)
(9)
а также xÎA÷BÞxÎAÙxÏB. (9а)
Пример 1.
Если E1={2; 4; 6} и E2={6; 8; 10}, то E3=E1÷E2={2; 4}, E4=E2÷E1={8;10}.
Пример 2.
Если M1={x1; x2; x3}, M2={y1; y2}, то M3=M1÷M2={ x1; x2; x3},
M4=M2÷M1={y1; y2}.
Пример 3.
Если K1={1; 3; 5; 7; 9}, K2={5; 7; 1}, то K3=K1÷K2={3; 9}, K4=K2÷K1=Æ.
Графическое представление вариантов разности двух множеств А и В показано на рис. 15÷18, где множество А ÷ В заштриховано.
| А |
| В |
| U |
| А |
| U |
| B |
| U |
| A\B=Ø |
| A=B |
| А |
| В |
| U |
рис. 15 рис. 16 рис. 17 рис. 18
Дополнение к множеству.
Определение 1.7
Пусть В Ì А. Множество всех элементов множества А, не принадлежащих множеству В, называют дополнением к множеству В и обозначают  или
или 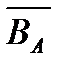 .
.
Если ясно, о каком множестве идёт речь, то индекс А опускается и пишут 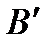 или
или  .
.
Определение 1.8
Пусть А – некоторое множество, являющееся частью универсального (основного) множества U. Дополнением множества А называется множество, состоящее из всех тех и только тех элементов их множества U, которые не принадлежат А. Его обозначают  или
или 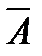 .
.
Это определение может быть записано в виде:
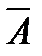 = {xïxÏA}. (10)
= {xïxÏA}. (10)
Графически дополнения (соответственно определениям 1.7 и 1.8) изображены на рис. 19 и 20 соответственно, на которых дополнения заштрихованы.
| A |
| B |
| A |
| U |
| U |
рис. 19 рис. 20
1. Множества.
Практические задания:
№3,4,5,6 (с.26).
2. Способы задания множеств.
Практические задания:
№2,7 (с. 28).
3. Подмножества. Диаграммы Эйлера-Венна.
Практические задания:
№1,6, 7 (с. 30).
4. Пересечение множеств.
Практические задания:
№1, 2, 3, 4, 7, 8 (с. 32-33).
5. Объединение множеств.
Практические задания:
№1,4 (с. 35).
6. Дополнение к подмножеству. Разность множеств.
Практические задания:
№1, ,5, 6 (с. 38).
Литература:
1. Виленкин Н.Я. и др. Математика: Учебное пособие длястудентов
педагогических институтов. -М.: Просвещение, 1977.
Практическое занятие 3
Комбинаторика
Комбинаторика — раздел математики, изучающий вопросы о том, сколько комбинаций определенного типа можно составить из данных предметов (элементов).
Как при решении задач с использованием классического определения вероятности, так и в дальнейшем нам понадобятся некоторые формулы комбинаторики. Приведем наиболее употребительные из них.
Определение 1. Размещениями из n различных элементов по m элементов (m≤n) называются комбинации, составленные из данных n элементов по m элементов, которые отличаются либо самими элементами, либо порядком элементов.
Например, из трех элементов а, b, с можно составить по два элемента следующие размещения:
ab, ас, bc, ba, ca, cb.
Число различных размещений из n элементов по m элементов определяется с помощью формулы

Пример 1. Сколько можно составить сигналов из 6 флажков различного цвета, взятых по 2? Искомое число сигналов 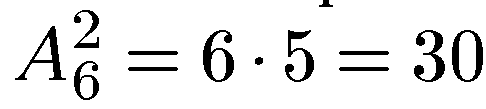 .
.
Определение 2. Перестановками из n различных элементов называются размещения из этих n элементов по n.
Как видно из определений 1 и 2, перестановки можно считать частным случаем размещений при m = n. Следовательно, число всех перестановок из n элементов вычисляется по формуле
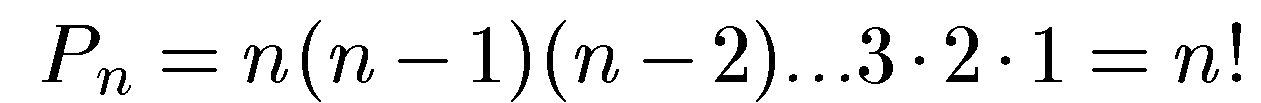
Пример 2. Для лечения заболевания применяют три лекарства. Полагают, что последовательность, в которой применяют лекарства, оказывает существенное влияние на результат лечения. Сколько имеется различных порядков назначения этих лекарств? Имеется  различных порядков назначения трех лекарств.
различных порядков назначения трех лекарств.
Определение 3. Сочетаниями из n различных элементов по m элементов называются комбинации, составленные из данных n элементов по m элементов, которые отличаются хотя бы одним элементом.
Отметим разницу между сочетаниями и размещениями: в первых не учитывается порядок элементов.
Число сочетаний из n элементов по m элементов вычисляется по формуле
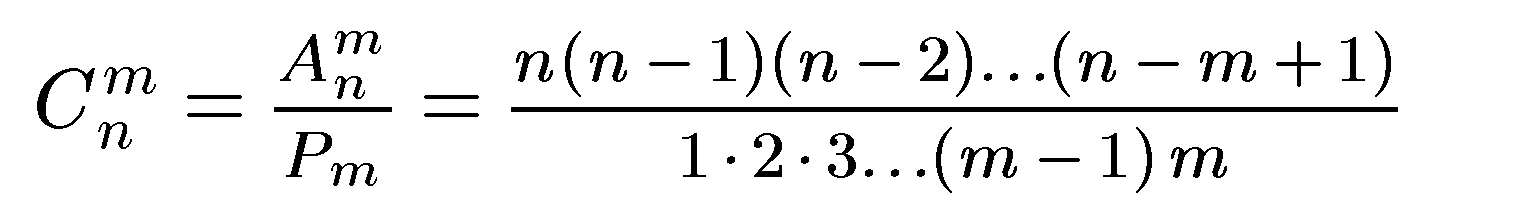
или

Отметим особенность формулы (1):
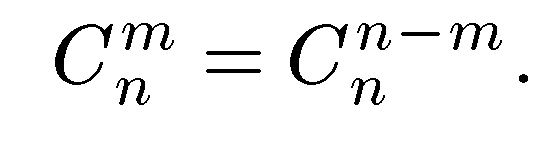
Пример 3. В лабораторной клетке содержат трех белых и трех коричневых мышей. Найти число способов выбора двух мышей, если они могут быть любого цвета.
В данном случае цвет не существен. Поэтому имеется 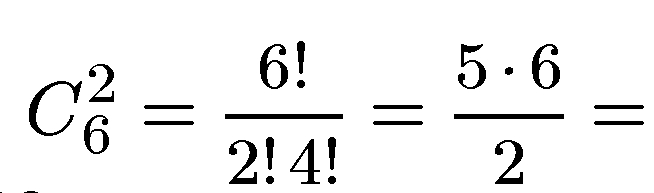 = 15 способов, которыми две мыши можно выбрать из шести.
= 15 способов, которыми две мыши можно выбрать из шести.
Приведем, наконец, один из примеров применения формул комбинаторики к нахождению вероятности события.
Пример 4. Набирая номер телефона, абонент забыл две последние цифры и, помня лишь, что эти цифры различны, набрал их наудачу. Какова вероятность того, что номер набран правильно?
Две последние цифры можно набрать 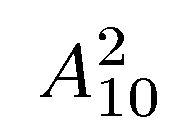 способами, а благоприятствовать событию М (цифры набраны правильно) будет только один способ. Поэтому
способами, а благоприятствовать событию М (цифры набраны правильно) будет только один способ. Поэтому
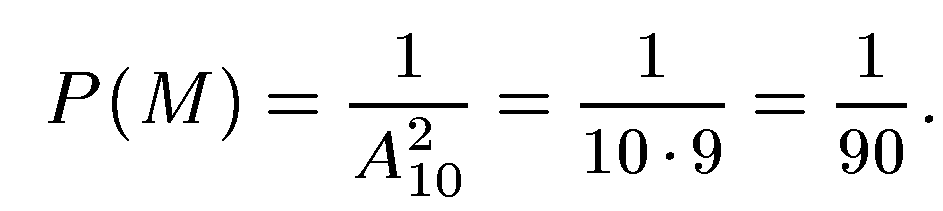
Практическое занятие 4
Дата добавления: 2018-02-28; просмотров: 383; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
